Problem Set 4
Due by 11:59 PM Sunday, October 11, 2020 by PDF upload in Blackboard Assignments
Please type your answers to the following questions in a document and save as a PDFIn MS Word, or Pages, or most word processing software, File -> Save As -> PDF, or File -> Export -> PDF.
to upload on Blackboard under Assignments. You may handwrite answers if you will be able to scan/photograph & convert them to a single PDF, if they are easily readable, but this is not preferred. See my guide to making a PDF - an essential skill in the modern world. If you are handwriting answers, you may print the pdf above and write on it, or just write on a piece of paper (we only need your answers).
You are part of a massive class. It will be much easier for us to grade, annotate, and return to you in a timely manner if your files are PDFs, so please save us some trouble. Thank you!
For the few questions that ask you to draw a graph, try to do so on your computer (use MS Paint, the drawing tools in MS Word or MS Powerpoint, plot points in MS Excel, drawing/notetaking apps, etc.), and save it as an image to include on your homework document. Again, they need not be perfect or to scale, just show that you understand the broad idea. Being able to understand and sketch the graphs is still a very important and useful skill! If all else fails, I will be lenient in grading graph questions if you are unable to technologically include a graph.
You may work together (and I highly encourage that) but you must turn in your own answers. Your TA, under my supervision, will grade homeworks 70% for completion, and for the remaining 30%, and one question will be graded for accuracy - so it is best that you try every problem, even if you are unsure how to complete it accurately.
Concepts and Critical Thinking
Please answer the following questions briefly (1-3 sentences). Use examples as necessary. Be sure to label graphs fully, if appropriate.
Question 1
What is the difference between accounting profit and economic profit? Is it possible for a firm to be profitable in an accounting sense but not an economic sense? Is it possible for a firm to be profitable in an economic sense but not an accounting sense?
Question 2
In a competitive industry, with identical firms (e.g. all firms have the same costs, there are no economic rents), why are profits normal (zero) in the long run?
Question 3
In a competitive industry, even among firms with significant cost differences (e.g. there are economic rents), why do profits tend to return to normal (0) in the long run?
Problems
Show all work for calculations. You may lose points, even if correct, for missing work. Be sure to label graphs fully, if appropriate.
Question 4
Frame de Art is an art framing shop in a small town. Frame de Art has one storefront (with a rent of $500/week), and can hire workers for $300/week per worker. The table below shows how output of framed art (in 100s/week) varies with the number of workers.
| Output (hundreds) | Labor |
|---|---|
| \(0\) | \(0\) |
| \(1\) | \(1\) |
| \(2\) | \(3\) |
| \(3\) | \(6\) |
| \(4\) | \(11\) |
| \(5\) | \(20\) |
Assuming labor is the only variable cost, make a table to calculate the average cost and marginal cost of 0, 1, 2, 3, 4, and 5 (hundred) framing jobs.
Question 5
Mike’s Bikes produces racing bicycles. Consider the following graph, which illustrates the short run average total cost curves corresponding to three possible plant sizes Mike could produce with: a small plant, a medium plant, and a large plant.
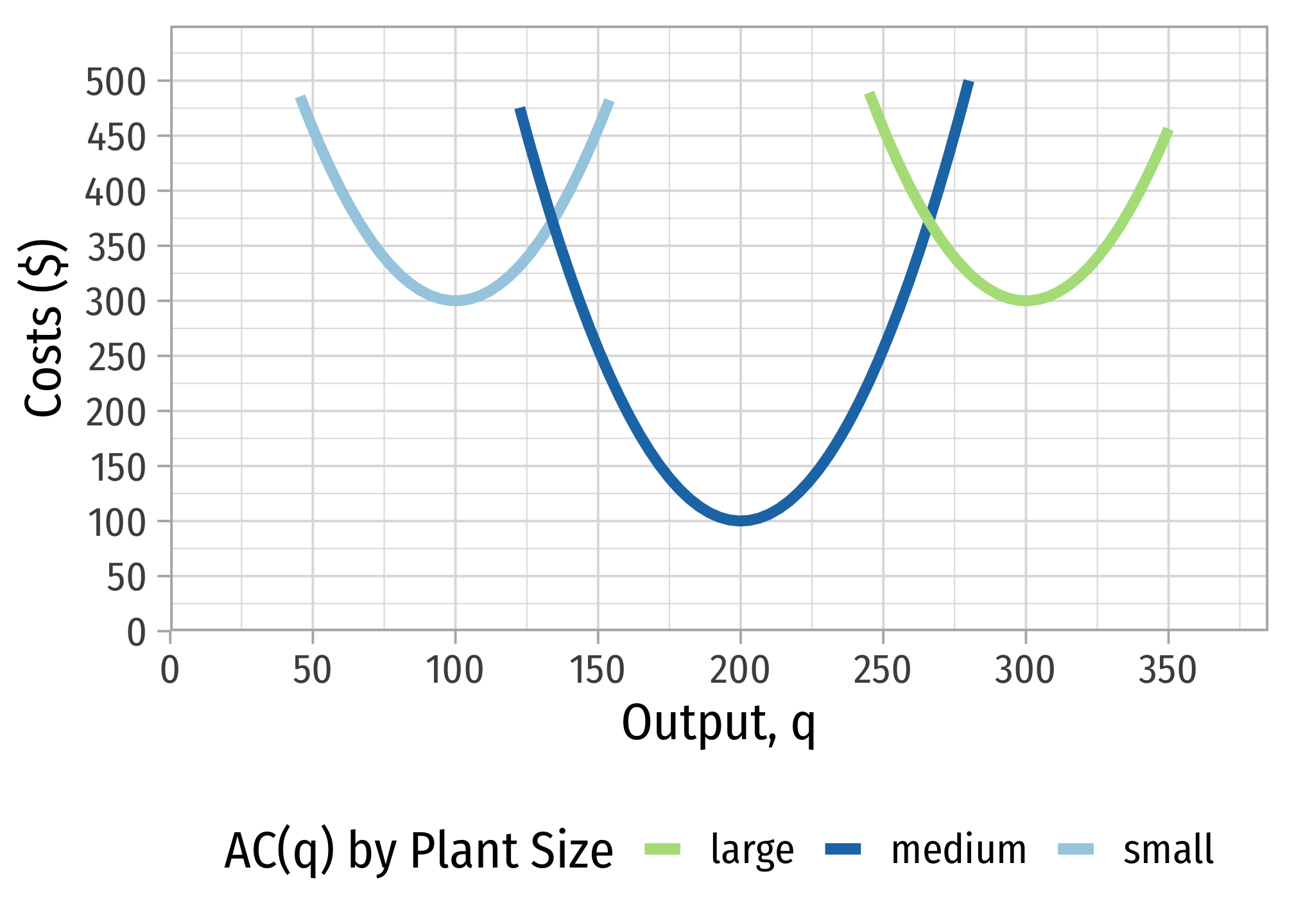
Part A
If Mike wanted to produce 125 bikes, what size plant should be used, and why? What about 150 bikes?
Part B
If Mike wanted to produce 250 bikes, what size plant should be used, and why? What about 275 bikes?
Part C
Draw the long run average cost curve on the graph provided (or sketch one yourself).
Part D
Suppose Mike’s long run total cost function can be roughly expressed as:
\[LRC(q)=\frac{1}{64}q^3-6.25q^2+725q\]
with a long run marginal cost function of
\[LRMC(q)=\frac{3}{64}q^2-12.5q+725\]
Find the quantity of bikes where long run average cost is minimized. Plot this point on your graph. At what range of production does Mike experience economies of scale? At what range of production does Mike experience diseconomies of scale?
Question 6
Daniel’s Midland Archers has the following cost structure for producing archery bows:
\[\begin{align*} C(q)&=2q^2+3q+50 \\ MC(q)&=4q+3\\ \end{align*}\]
Part A
Write an equation for fixed costs, \(f\).
Part B
Write an equation for variable costs, \(VC(q)\).
Part C
Write an equation for average fixed costs, \(AFC(q)\).
Part D
Write an equation for average variable costs, \(AVC(q)\).
Part E
Write an equation for average (total) costs, \(AC(q)\).
Part F
At what price does Daniel’s Midland Archers break even?
Part G
Below what price would Daniel’s Midland Archers shut down in the short-run?
Part H
Write an equation for the firm’s short-run inverse supply curve, and sketch a rough graph.
Part I
What differences would there be between how Daniel’s Midland Archers decides to produce in the short run versus the long run?
Part J
In the long run, with many identical sellers of archery bows, what would be the equilibrium price?
Question 7
Assume that consumers view tax preparation services as undifferentiated among producers, and that there are hundreds of companies offering tax preparation in a given market. The current market equilibrium price is $120. Joe Audit’s Tax Service has a daily short-run cost structure given by
\[\begin{align*} C(q)&=100+4q^2 \\ MC(q)&=8q\\ \end{align*}\]
Part A
How many tax returns should Joe prepare each day if his goal is to maximize profits?
Part B
How much profit will he earn each day?
Part C
At what market price would Joe break even?
Part D
Below what hypothetical price would Joe shut down in the short run?