+ - 0:00:00
Notes for current slide
Notes for next slide

1.5 — Solving the Consumer’s Problem

ECON 306 • Microeconomic Analysis • Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microF20
microF20.classes.ryansafner.com

The Consumer's Problem: Review

  • The consumer's constrained optimization problem is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

  3. Subject to: < income and market prices >

The Consumer's Problem: Tools

  • We now have the tools to understand consumer choices:

  • Budget constraint: consumer's constraints of income and market prices

    • How the market trades off between two goods
  • Utility function: consumer's preferences to maximize
    • How the consumer trades off between two goods

The Consumer's Problem: Verbally

  • The consumer's constrained optimization problem:

choose a bundle of goods to maximize utility, subject to income and market prices

The Consumer's Problem: Mathematically

maxx,yu(x,y)

s.t.pxx+pyy=m

  • This requires calculus to solve1. We will look at graphs instead!

1 See the mathematical appendix in today's class notes on how to solve it with calculus, and an example.

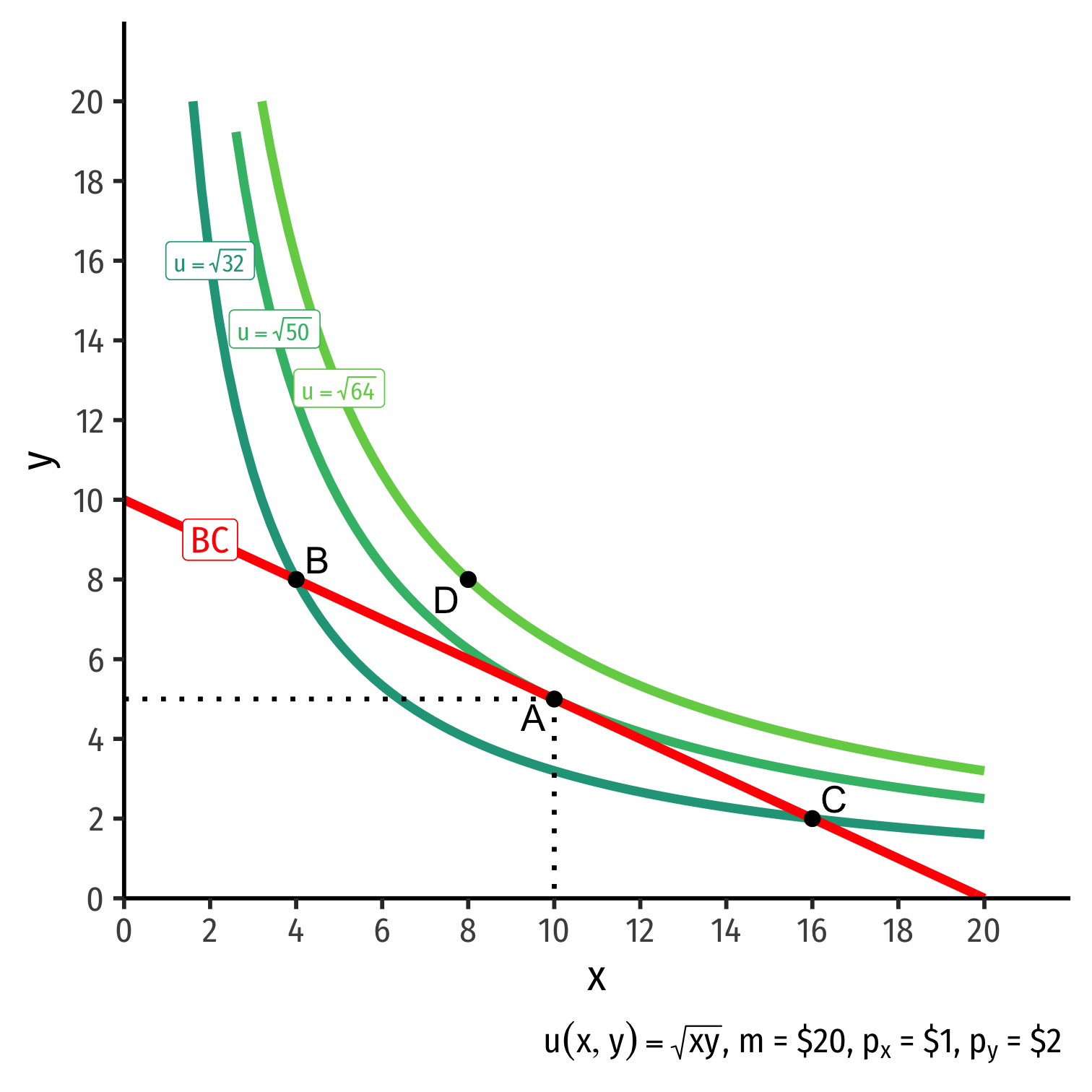
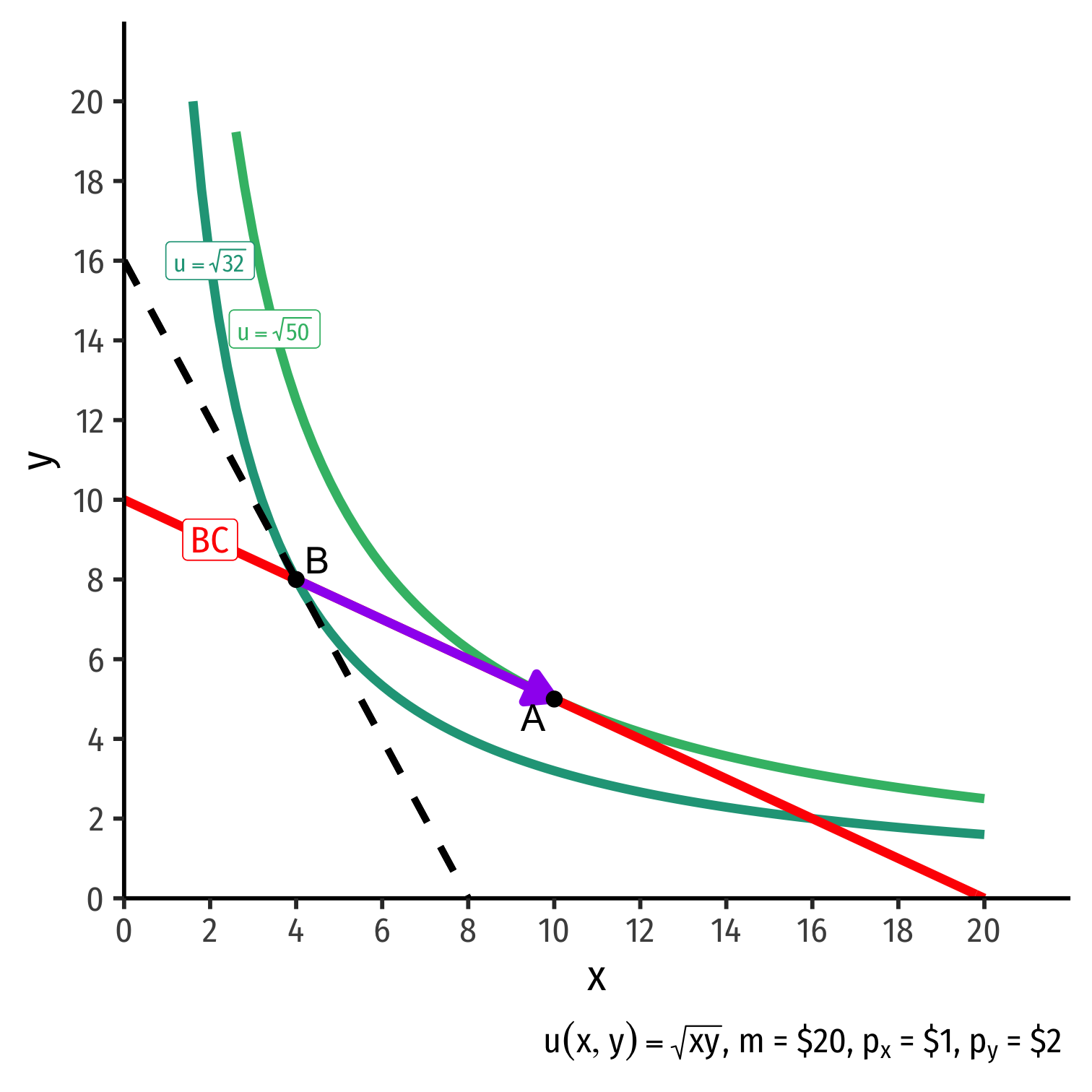
The Consumer's Optimum: Graphically

  • Graphical solution: Highest indifference curve tangent to budget constraint
    • Bundle A!

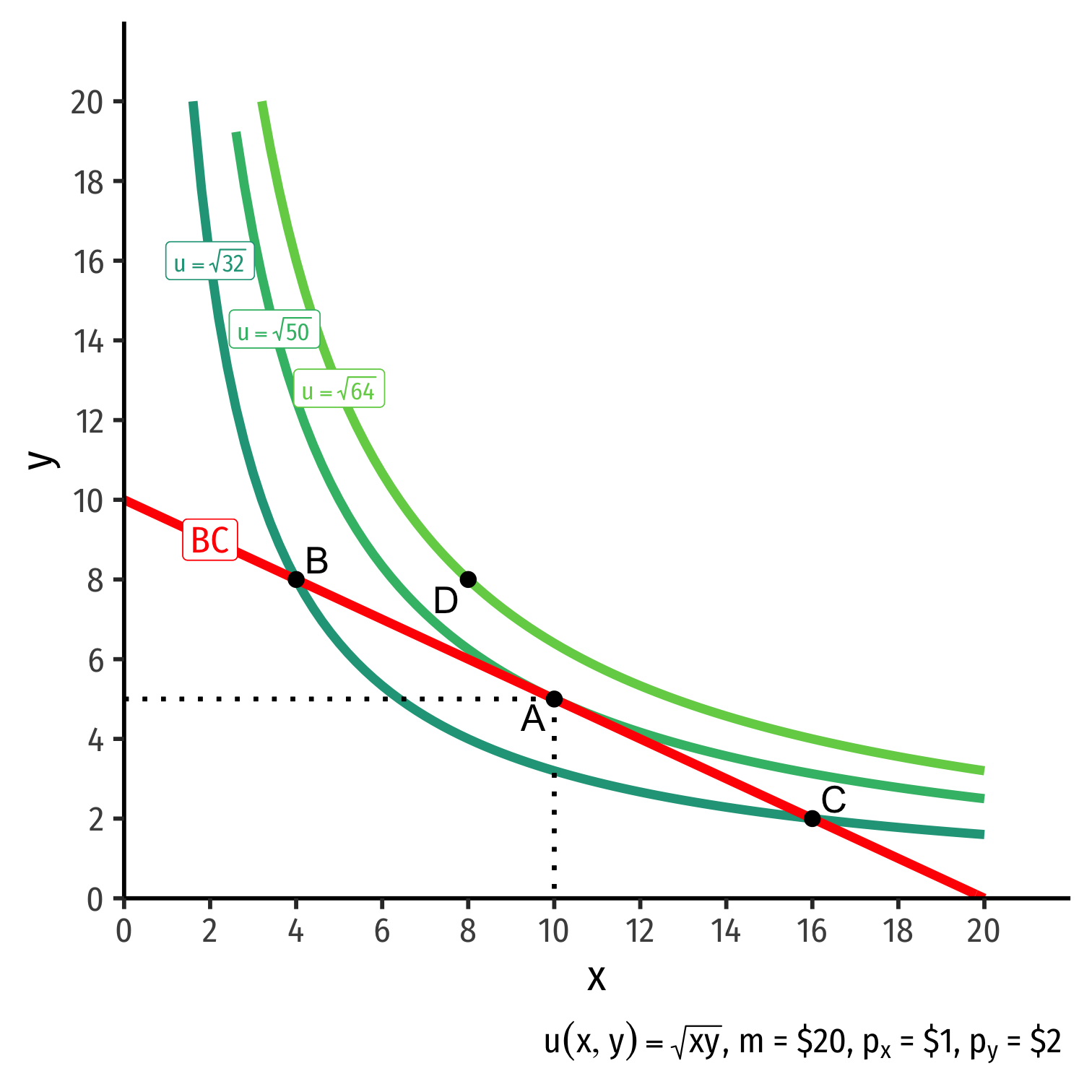
The Consumer's Optimum: Graphically

  • Graphical solution: Highest indifference curve tangent to budget constraint

    • Bundle A!

  • B or C spend all income, but a better combination exists

    • Averages ≻ extremes!

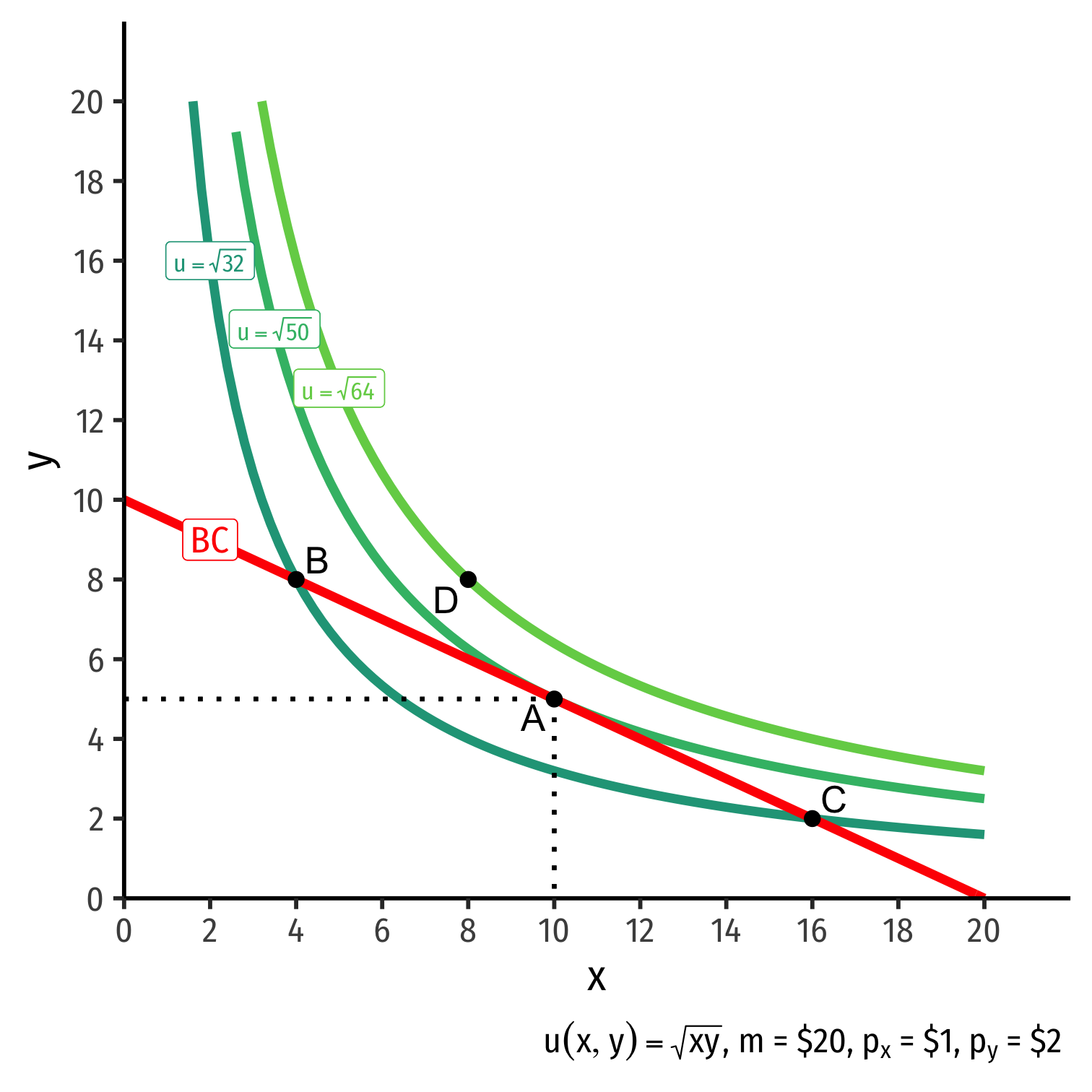
The Consumer's Optimum: Graphically

  • Graphical solution: Highest indifference curve tangent to budget constraint

    • Bundle A!

  • B or C spend all income, but a better combination exists

    • Averages ≻ extremes!

  • D is higher utility, but not affordable at current income & prices

The Consumer's Optimum: Why Not B?

indiff. curve slope>budget constr. slope

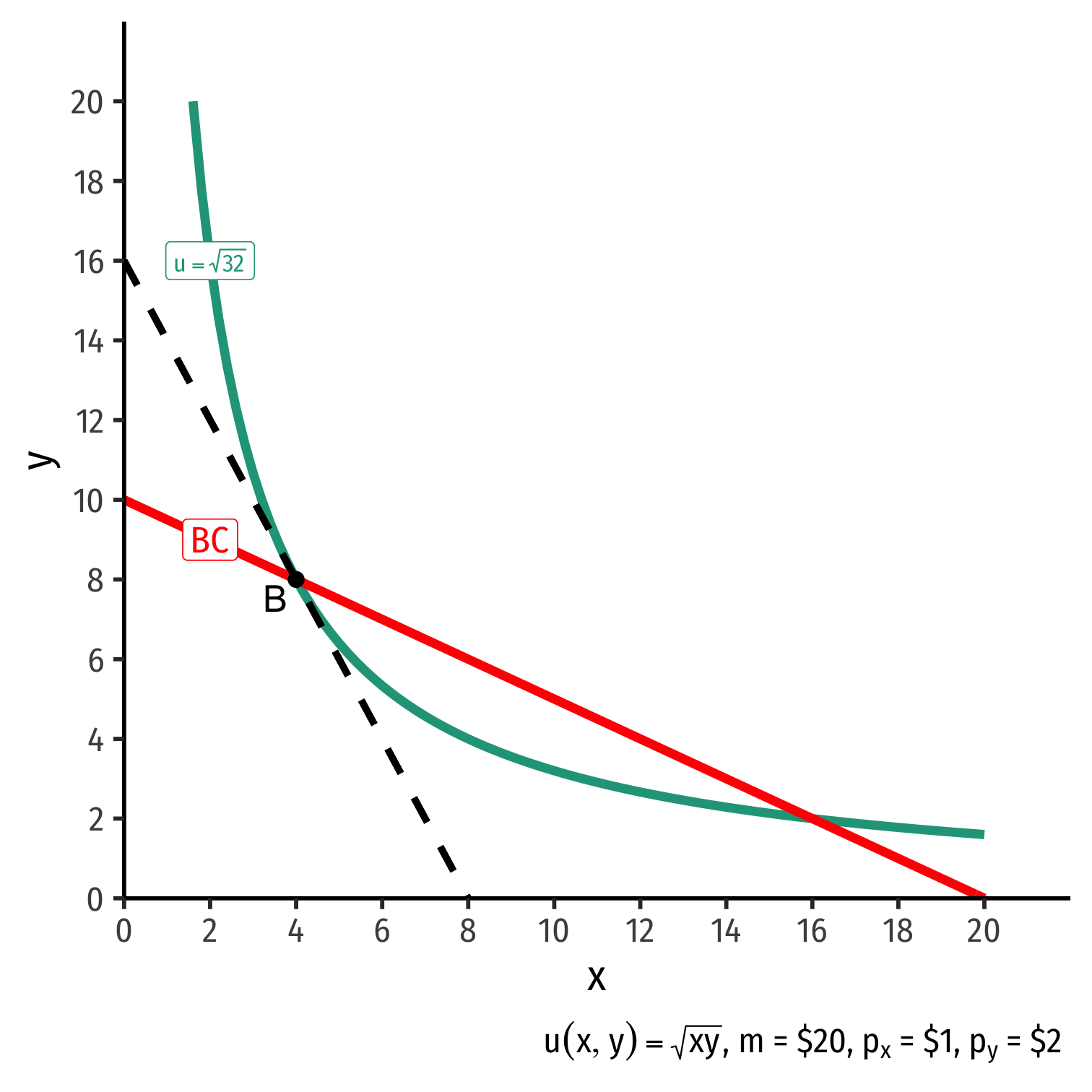
The Consumer's Optimum: Why Not B?

indiff. curve slope>budget constr. slope|MRSx,y|>|pxpy||MUxMUy|>|pxpy||−2|>|−0.5|

  • Consumer would exchange at 2Y:1X

  • Market exchange rate is 0.5Y:1X

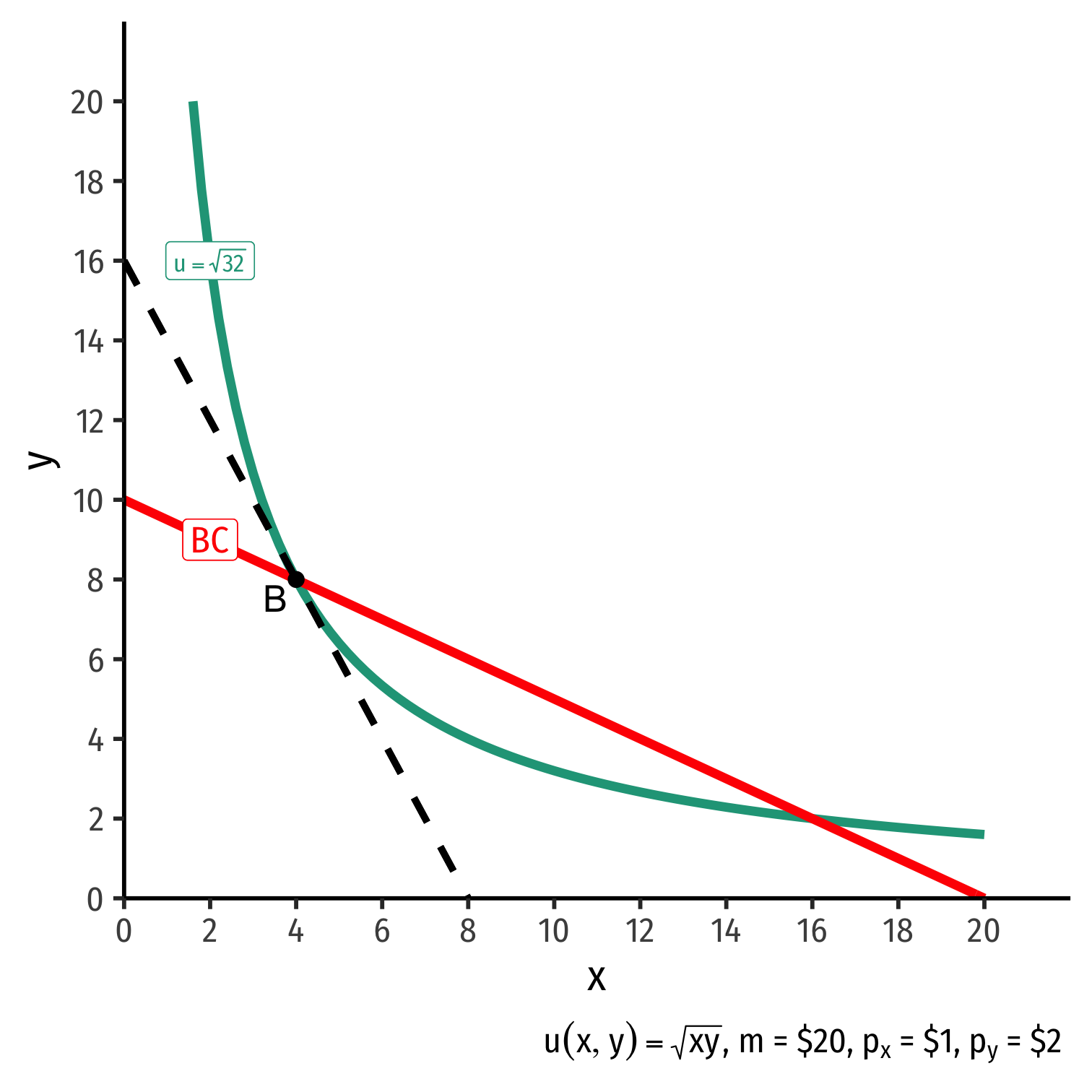
The Consumer's Optimum: Why Not B?

indiff. curve slope>budget constr. slope|MRSx,y|>|pxpy||MUxMUy|>|pxpy||−2|>|−0.5|

  • Consumer would exchange at 2Y:1X

  • Market exchange rate is 0.5Y:1X

  • Can spend less on y more on x and get more utility!

The Consumer's Optimum: Why Not C?

indiff. curve slope<budget constr. slope

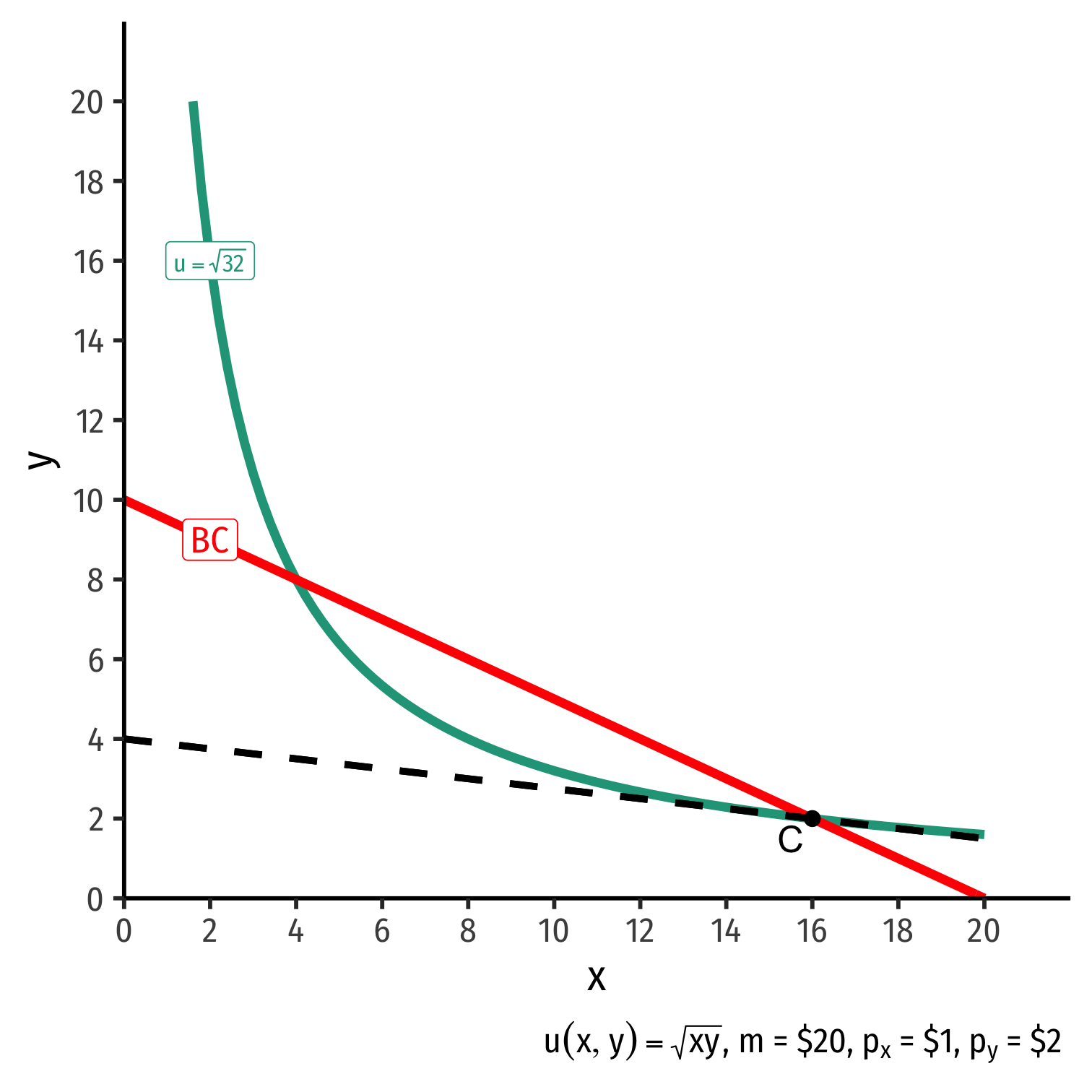
The Consumer's Optimum: Why Not C?

indiff. curve slope<budget constr. slope|MRSx,y|<|pxpy||MUxMUy|<|pxpy||−0.125|<|−0.5|

  • Consumer would exchange at 0.125Y:1X

  • Market exchange rate is 0.5Y:1X

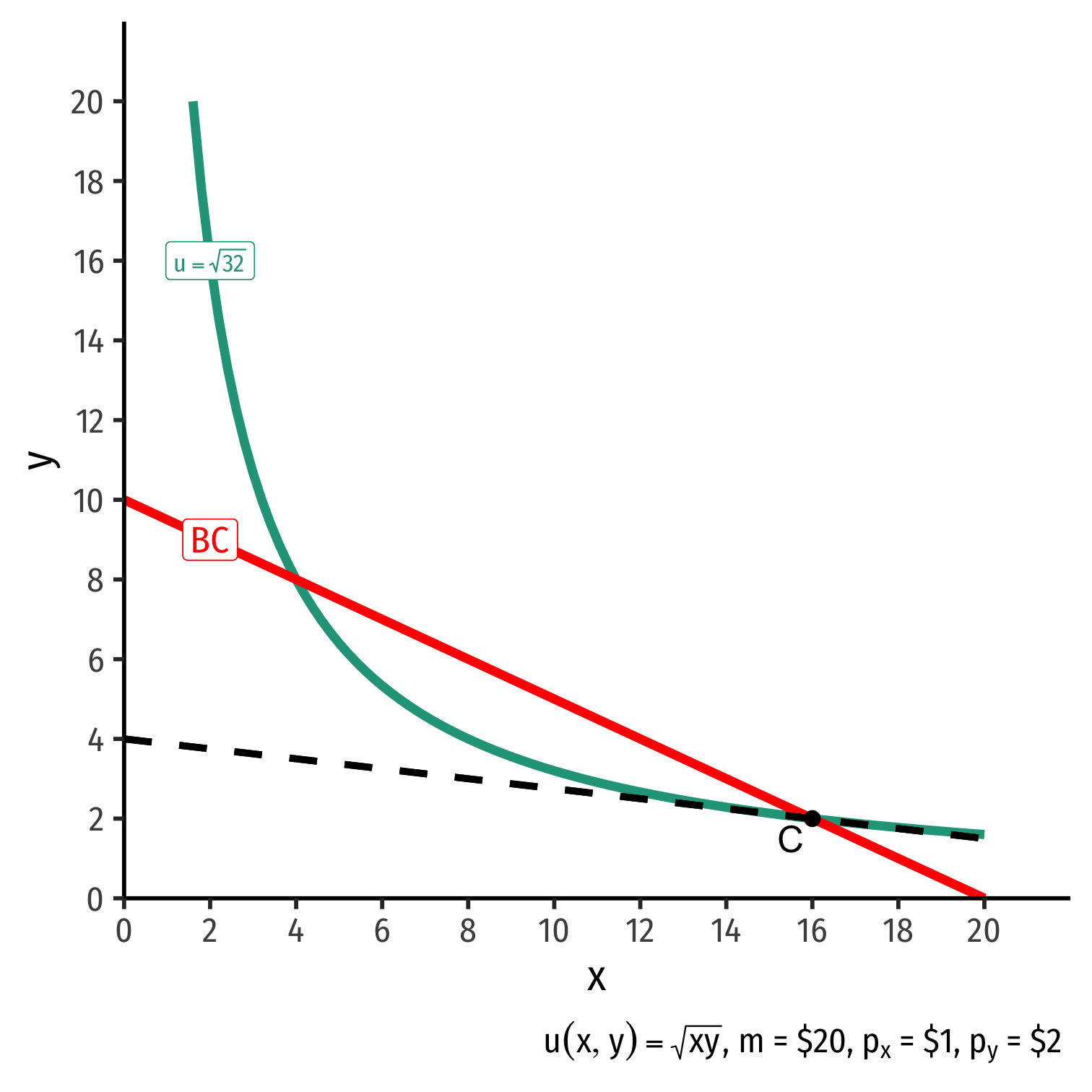
The Consumer's Optimum: Why Not C?

indiff. curve slope<budget constr. slope|MRSx,y|<|pxpy||MUxMUy|<|pxpy||−0.125|<|−0.5|

  • Consumer would exchange at 0.125Y:1X

  • Market exchange rate is 0.5Y:1X

  • Can spend less on x, more on y and get more utility!

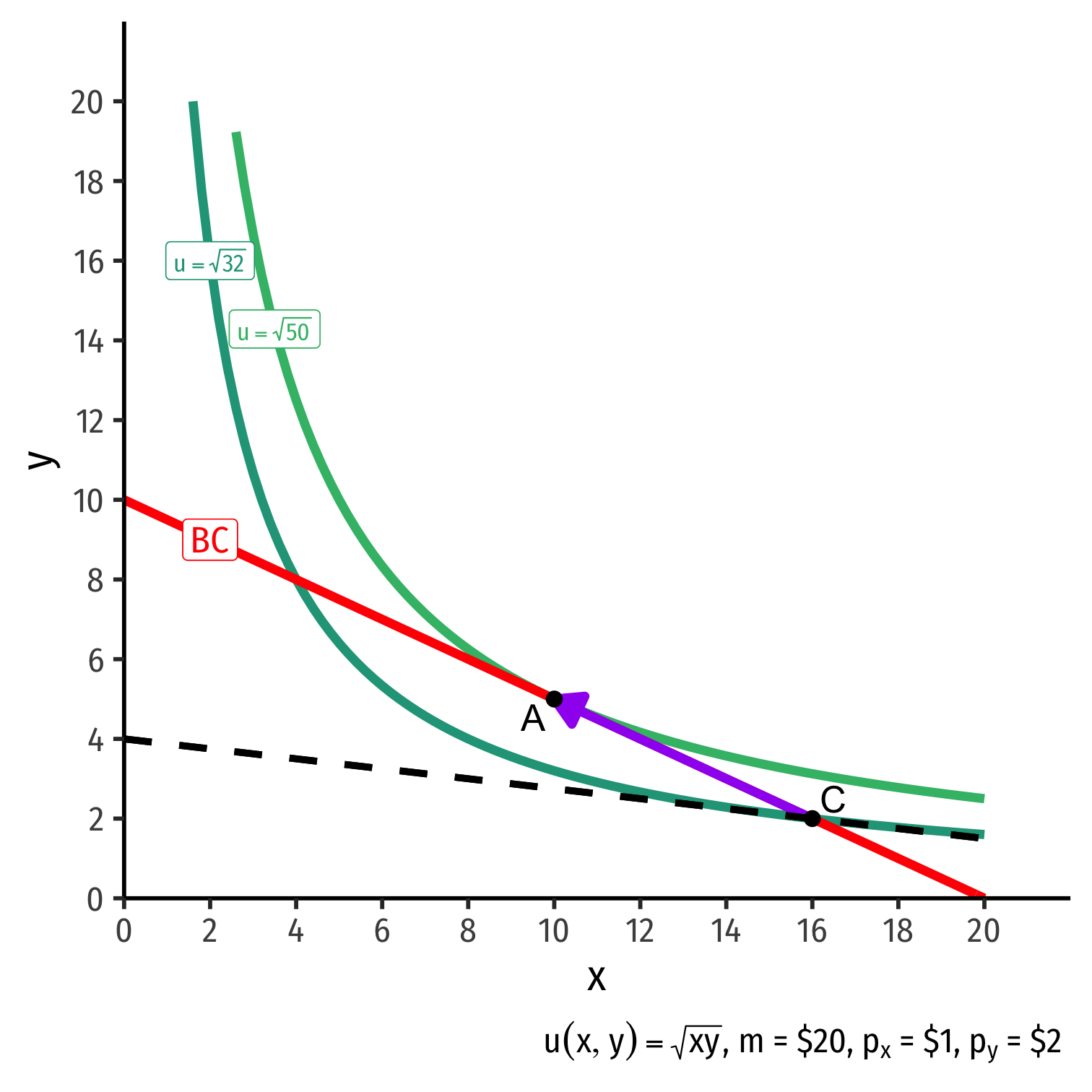
The Consumer's Optimum: Why A?

indiff. curve slope=budget constr. slope

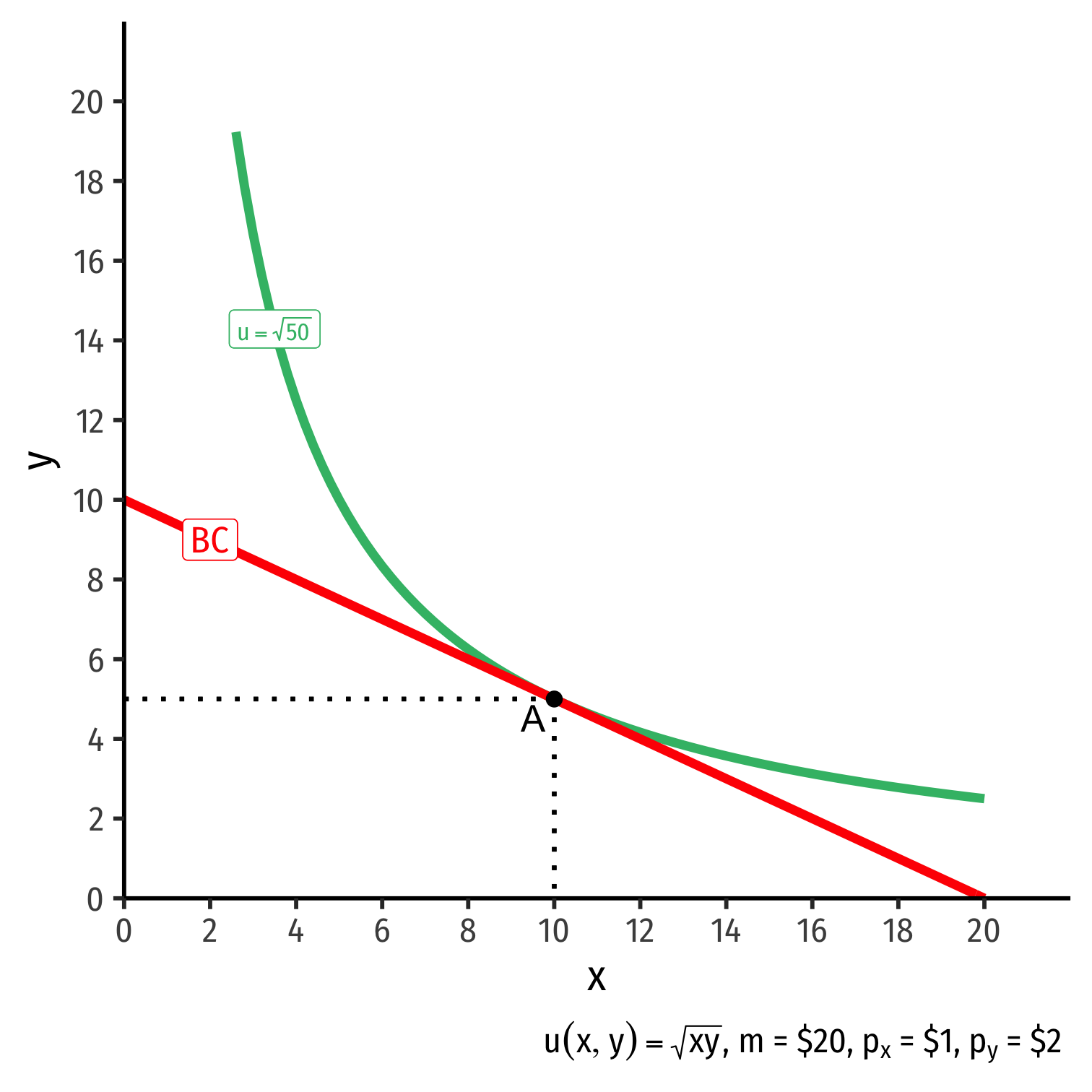
The Consumer's Optimum: Why A?

indiff. curve slope=budget constr. slope|MRSx,y|=|pxpy||MUxMUy|=|pxpy||−0.5|=|−0.5|

  • Consumer would exchange at same rate as market

  • No other combination of (x,y) exists at current prices & income that could increase utility!

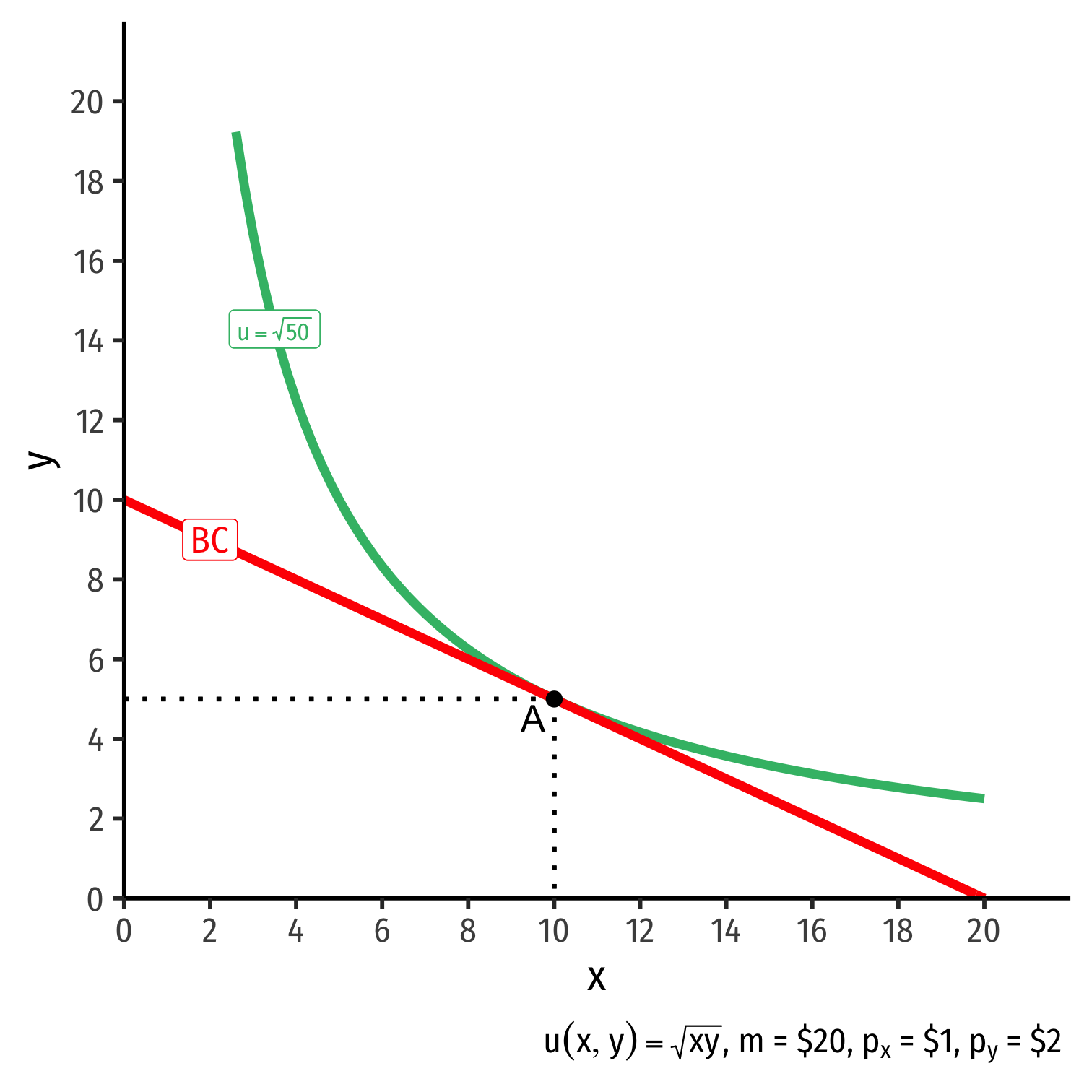
The Consumer's Optimum: Two Equivalent Rules

Rule 1

MUxMUy=pxpy

  • Easier for calculation (slopes)

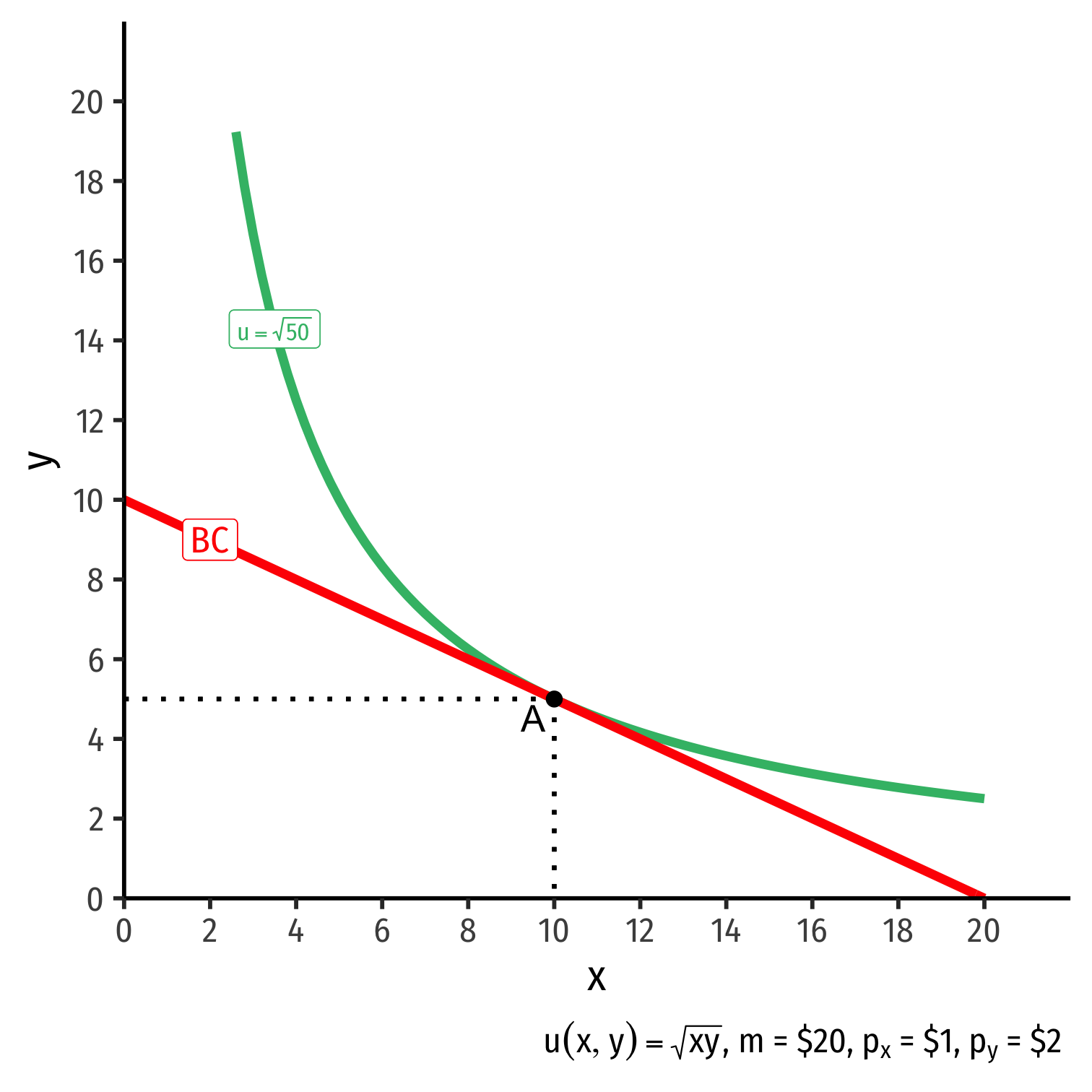
The Consumer's Optimum: Two Equivalent Rules

Rule 1

MUxMUy=pxpy

  • Easier for calculation (slopes)

Rule 2

MUxpx=MUypy

  • Easier for intuition (next slide)

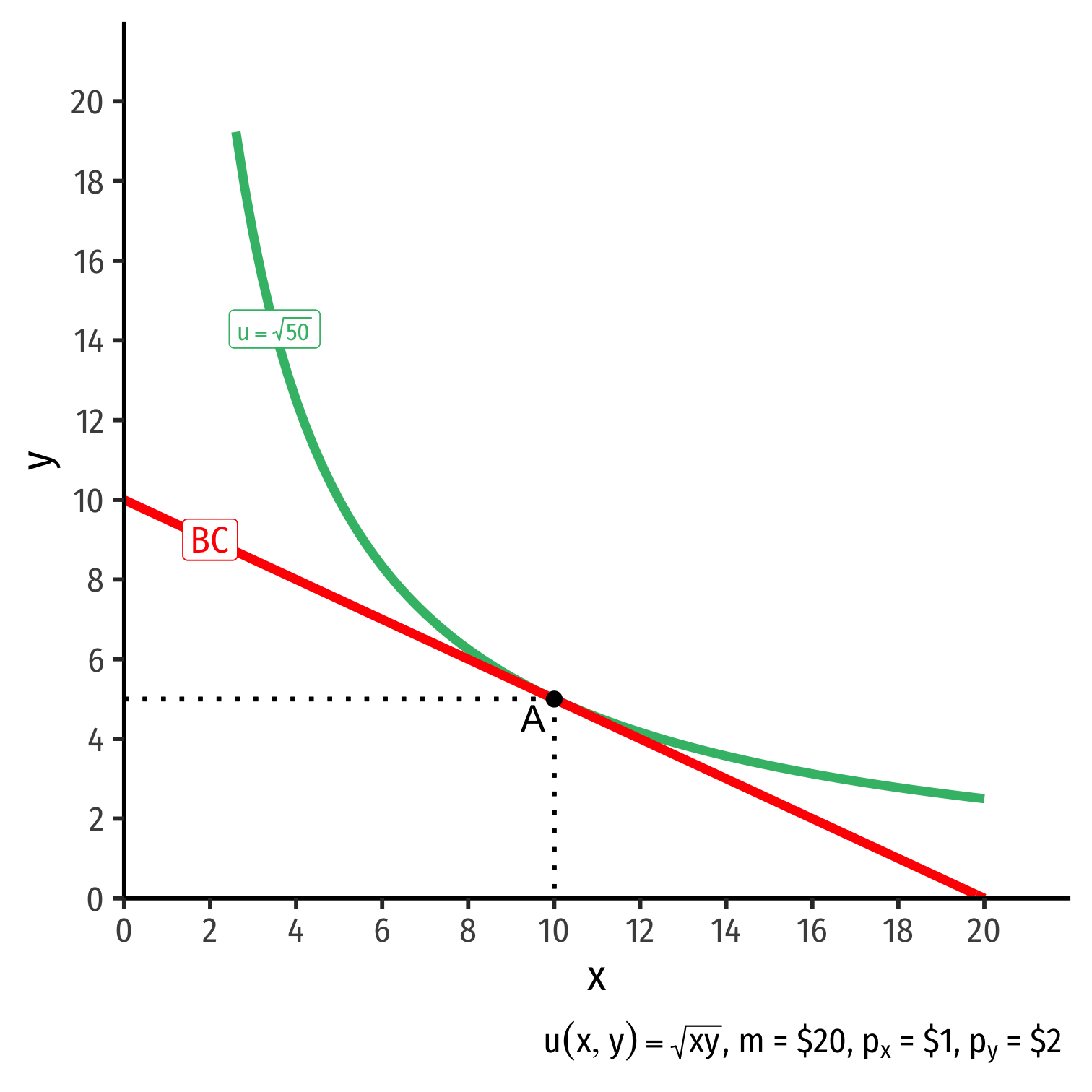
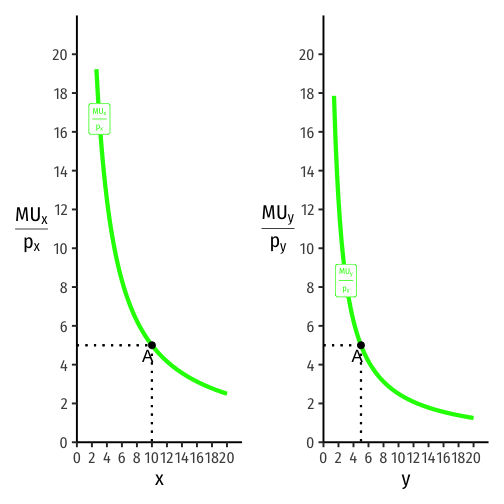
Visualizing the Equimarginal Rule

  • Compare MUx per $1 spent vs. MUy per $1 spent
    • Graphs on right are not indifference curves!

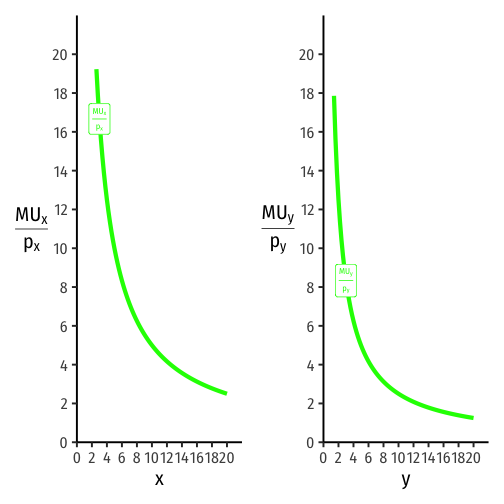
Visualizing the Equimarginal Rule

  • Suppose you consume 4 of x and 12.5 of y (points B)

MUxpx>MUypy

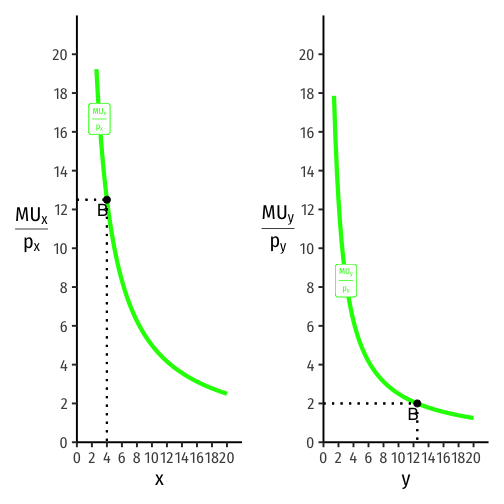
Visualizing the Equimarginal Rule

  • Suppose you consume 4 of x and 12.5 of y (points B)

MUxpx>MUypy

  • More "bang for your buck" with x than y

  • Consume more x, less y!

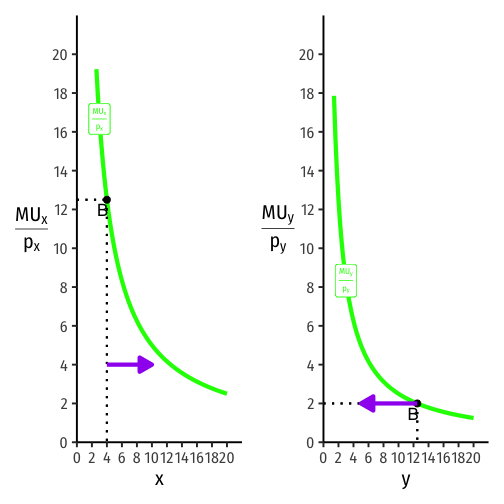
Visualizing the Equimarginal Rule

  • At points A, consuming 10 of x and 5 of y

MUxpx=MUypy

  • No change (more x, less x, more y, less y) that could increase your utility!

  • The optimum! Cost-adjusted marginal utilities are equalized

The Consumer's Optimum: The Equimarginal Rule I

MUxpx=MUypy=⋯=MUnpn

  • Equimarginal Rule: consumption is optimized where the marginal utility per dollar spent is equalized across all n possible goods/decisions

  • You will always choose an option that gives higher marginal utility (e.g. if MUx>MUy)

    • But each option has a different cost, so we weight each option by its cost, hence MUxpx

The Consumer's Optimum: The Equimarginal Rule II

  • Any optimum in economics: no better alternatives exist under current constraints

  • No possible change in your consumption that would increase your utility

Markets Equalize Everyone's MRS I

  • Markets make it so everyone faces the same relative prices

    • Budget constraint. slope, −pxpy
    • Note individuals' incomes, m, are certainly different!

  • A person's optimal choice ⟹ they make same tradeoff as the market

    • Their MRS = relative price ratio

  • markets equalize everyone's MRS

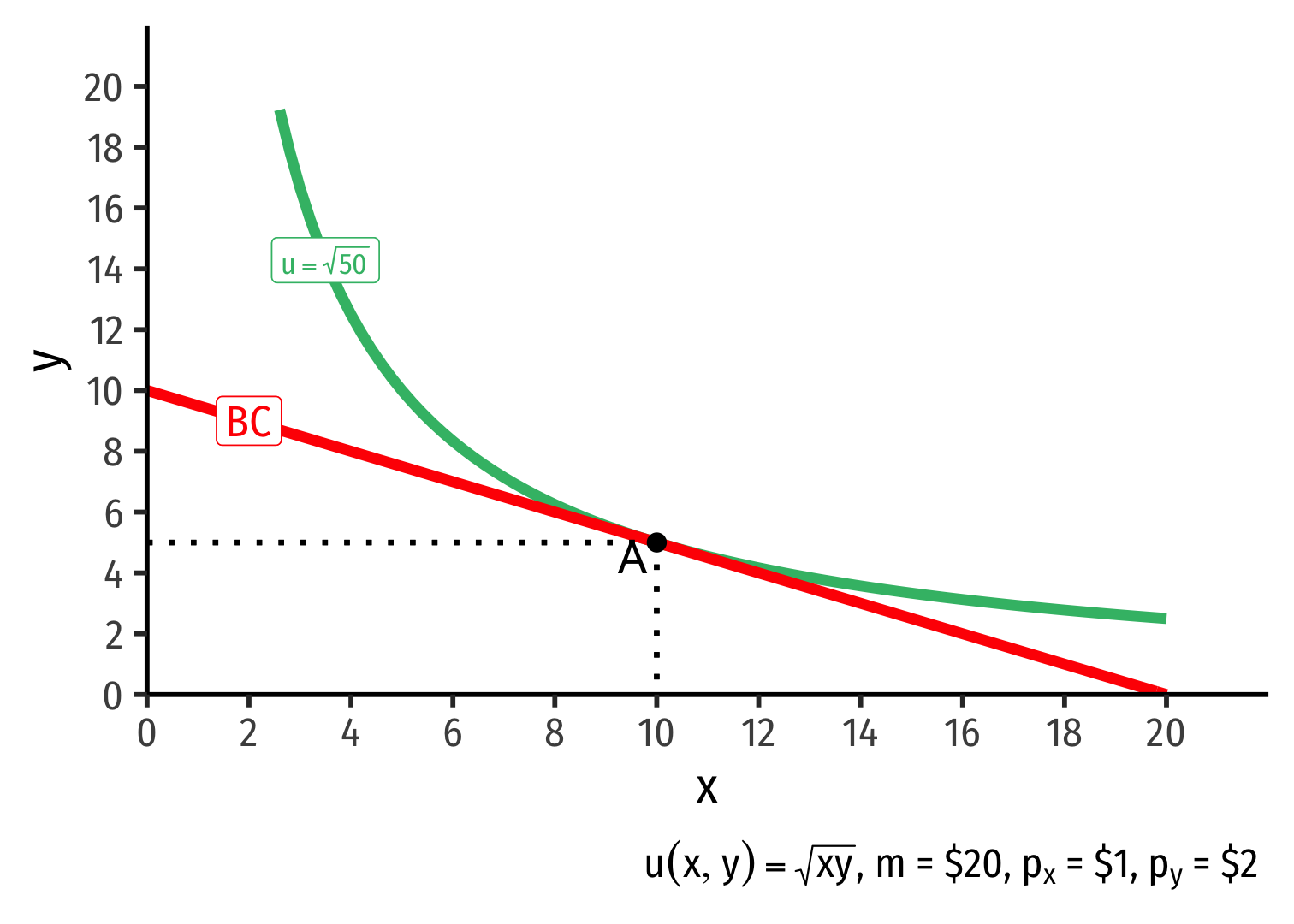
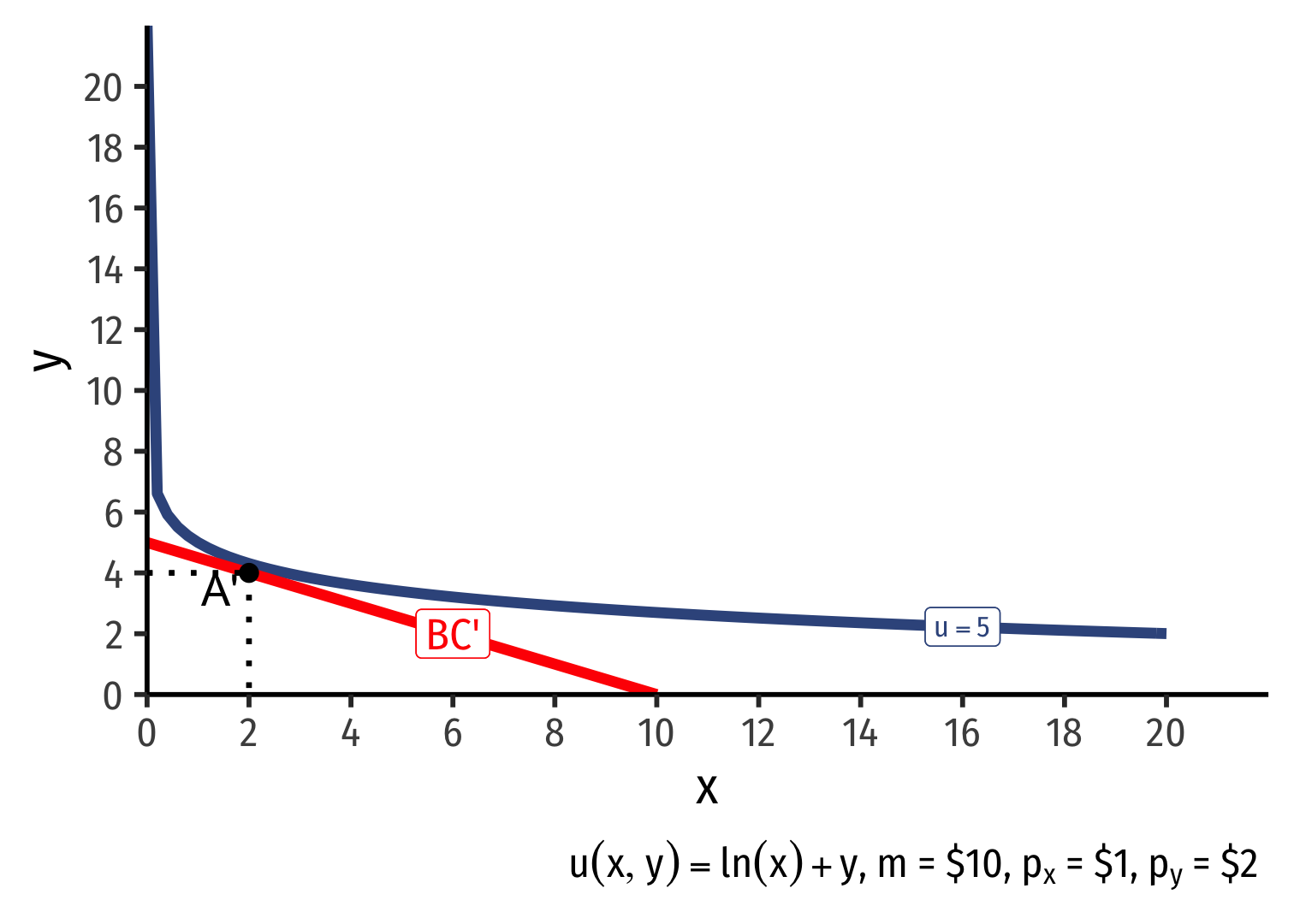
Markets Equalize Everyone's MRS II

Two people will very different income and preferences face the same market prices, and choose optimal consumption (points A and A') at an exchange rate of 0.5Y:1X

Optimization and Equilibrium

  • If people can learn and change their behavior, they will always switch to a higher-valued option

  • If a person has no better choices (under current constraints), they are at an optimum

  • If everyone is at an optimum, the system is in equilibrium

Practice I

Example: You can get utility from consuming bags of Almonds (a) and bunches of Bananas (b), according to the utility function:

u(a,b)=abMUa=bMUb=a

You have an income of $50, the price of Almonds is $10, and the price of Bananas is $2. Put Almonds on the horizontal axis and Bananas on the vertical axis.

  1. What is your utility-maximizing bundle of Almonds and Bananas?
  2. How much utility does this provide? [Does the answer to this matter?]

Practice II, Cobb-Douglas!

Example: You can get utility from consuming Burgers (b) and Fries (f), according to the utility function:

u(b,f)=√bfMUb=0.5b−0.5f0.5MUf=0.5b0.5f−0.5

You have an income of $20, the price of Burgers is $5, and the price of Fries is $2. Put Burgers on the horizontal axis and Fries on the vertical axis.

  1. What is your utility-maximizing bundle of Burgers and Fries?
  2. How much utility does this provide?

The Consumer's Problem: Review

  • The consumer's constrained optimization problem is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

  3. Subject to: < income and market prices >

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow