+ - 0:00:00
Notes for current slide
Notes for next slide

1.7 — Income & Substitution Effects

ECON 306 • Microeconomic Analysis • Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microF20
microF20.classes.ryansafner.com

A Demand Function (Again)

  • A consumer's demand (for good x) depends on current prices & income:

qDx=qDx(m,px,py)

  • How does demand for x change?
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income
  2. Cross-price effects (ΔqDxΔpy): how qDx changes with changes in prices of other goods (e.g. y)
  3. (Own) Price effects (ΔqDxΔpx): how qDx changes with changes in price (of x)

The (Own) Price Effect

The (Own) Price Effect

  • Price effect: change in optimal consumption of a good associated with a change in its price, holding income and other prices constant

ΔqDxΔpx<0

The law of demand: as the price of a good rises, people will tend to buy less of that good (and vice versa)

  • i.e. the price effect is negative!

Decomposing the Price Effect

The price effect (law of demand) is actually the net result of two effects

Decomposing the Price Effect

The price effect (law of demand) is actually the net result of two effects

  1. (Real) income effect: change in consumption due to change in real purchasing power

Decomposing the Price Effect

The price effect (law of demand) is actually the net result of two effects

  1. (Real) income effect: change in consumption due to change in real purchasing power

  2. Substitution effect: change in consumption due to change in relative prices

Decomposing the Price Effect

The price effect (law of demand) is actually the net result of two effects

  1. (Real) income effect: change in consumption due to change in real purchasing power

  2. Substitution effect: change in consumption due to change in relative prices

Price Effect = Real income effect + Substitution Effect

(Real) Income Effect

(Real) Income Effect: Demonstration

  • Suppose there is only 1 good to consume, x. You have a $100 income, and the price of x is $10. You consume 10 units of x

  • Suppose the price of x falls to $5. Your now consume 20 units of x.

  • This is the real income effect

(Real) Income Effect: Demonstration

  • Real income effect: your consumption mix changes because of the change in the price of x changes your real income or purchasing power (the amount of goods you can buy)

  • Note your actual (nominal) income ($100) never changed!

(Real) Income Effect: Size

  • The size of the income effect depends on how large a portion of your budget you spend on the good

  • Large-budget items:

    • e.g. Housing/apartment rent, car prices
    • Price increase makes you much poorer
    • Price decrease makes you much wealthier

(Real) Income Effect: Size

  • The size of the income effect depends on how large a portion of your budget you spend on the good

  • Small-budget items:

    • e.g. pencils, toothpicks, candy
    • Price changes don't have much of an effect on your wealth or change your behavior much

Substitution Effect

Substitution Effect: Demonstration

  • Suppose there are 1000's of goods, none of them a major part of your budget

    • So real income effect is insignificant

  • Suppose the price of one good, x increases

  • You would consume less of x relative to other goods because x is now relatively more expensive

  • That's the substitution effect

Substitution Effect: Demonstration

  • Substitution effect: consumption mix changes because of a change in relative prices

  • Buy more of the (now) relatively cheaper items

  • Buy less of the (now) relatively more expensive item (x)

Putting the Effects Together

Putting the Effects Together

  • Real income effect: change in consumption due to change in real purchasing power
    • Can be positive (normal goods) or negative (inferior goods)
    • Lower price of x means you can buy more x, y, or both (depending on your preferences between x and y)

Putting the Effects Together

  • Real income effect: change in consumption due to change in real purchasing power
    • Can be positive (normal goods) or negative (inferior goods)
    • Lower price of x means you can buy more x, y, or both (depending on your preferences between x and y)
  • Substitution effect: change in consumption due to change in relative prices
    • If x gets cheaper relative to y, consume ↓y (and ↑x)
    • This is always the same direction! (↓ relatively expensive goods, uparrow relatively cheaper goods)
    • This is why demand curves slope downwards!

Putting the Effects Together

  • Real income effect: change in consumption due to change in real purchasing power
    • Can be positive (normal goods) or negative (inferior goods)
    • Lower price of x means you can buy more x, y, or both (depending on your preferences between x and y)
  • Substitution effect: change in consumption due to change in relative prices
    • If x gets cheaper relative to y, consume ↓y (and ↑x)
    • This is always the same direction! (↓ relatively expensive goods, uparrow relatively cheaper goods)
    • This is why demand curves slope downwards!

Price Effect = Real income effect + Substitution Effect

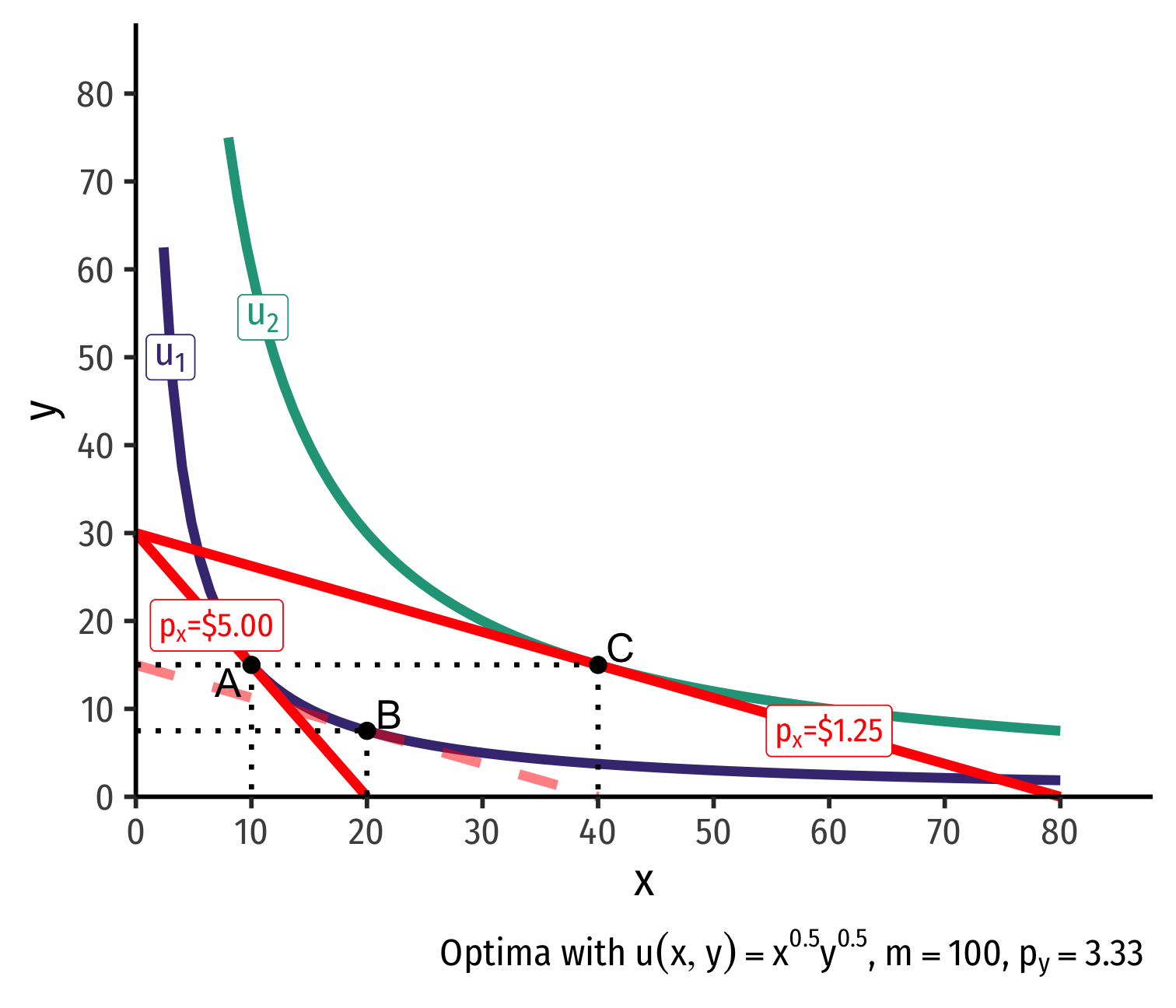
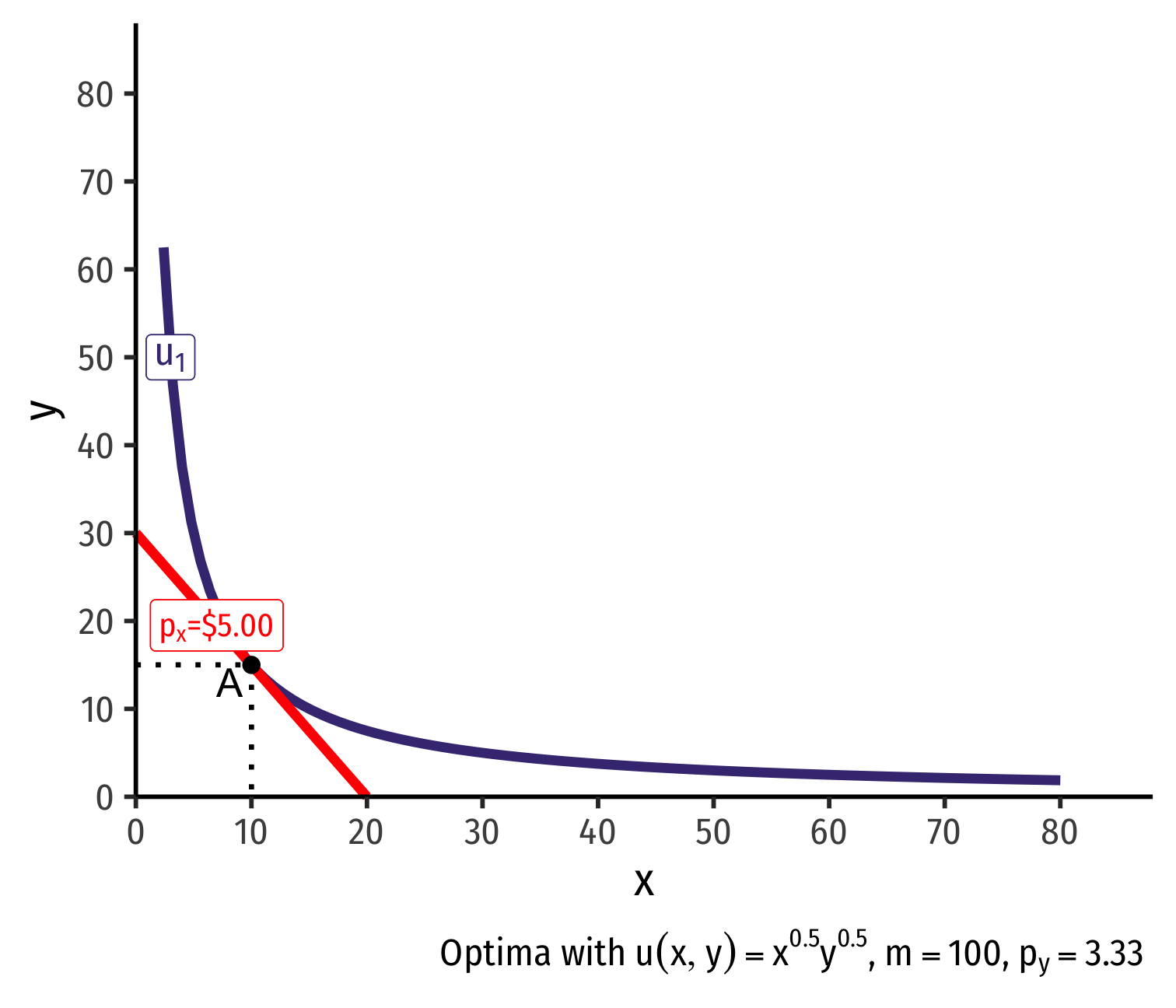
Real Income and Substitution Effects, Graphically I

  • Original optimal consumption (A)

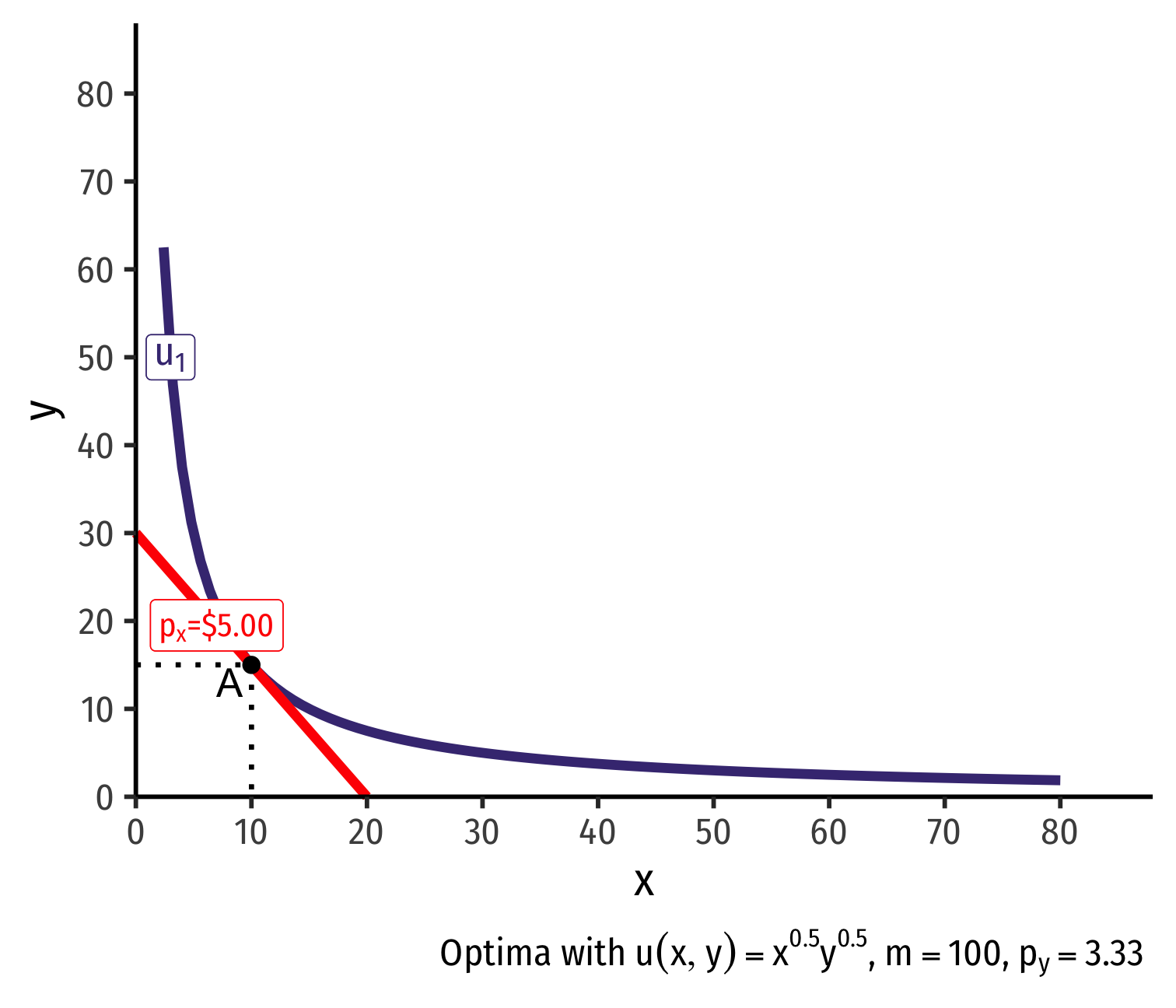
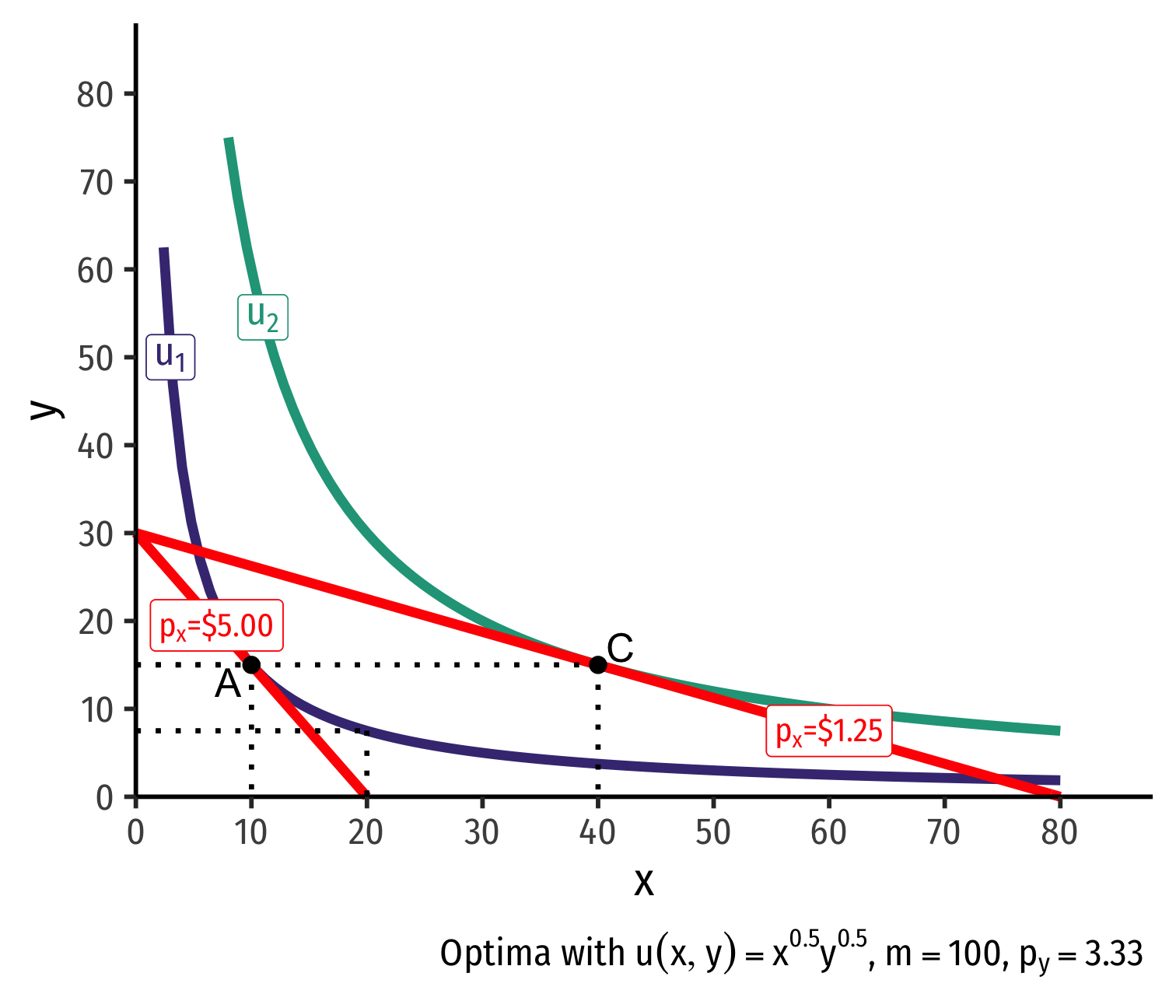
Real Income and Substitution Effects, Graphically I

  • Original optimal consumption (A)

  • (Total) price effect: A→C

  • Let's decompose this into the two effects

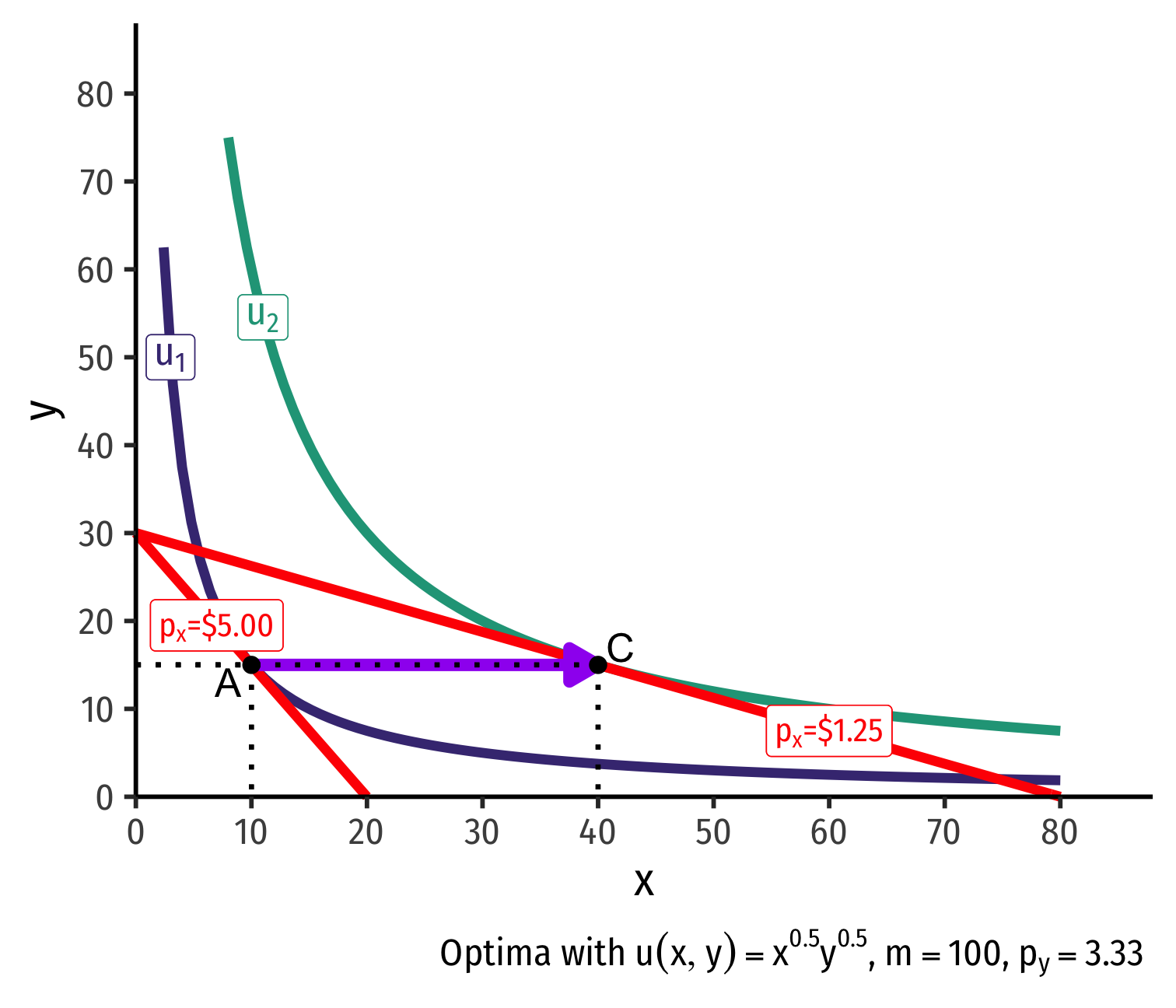
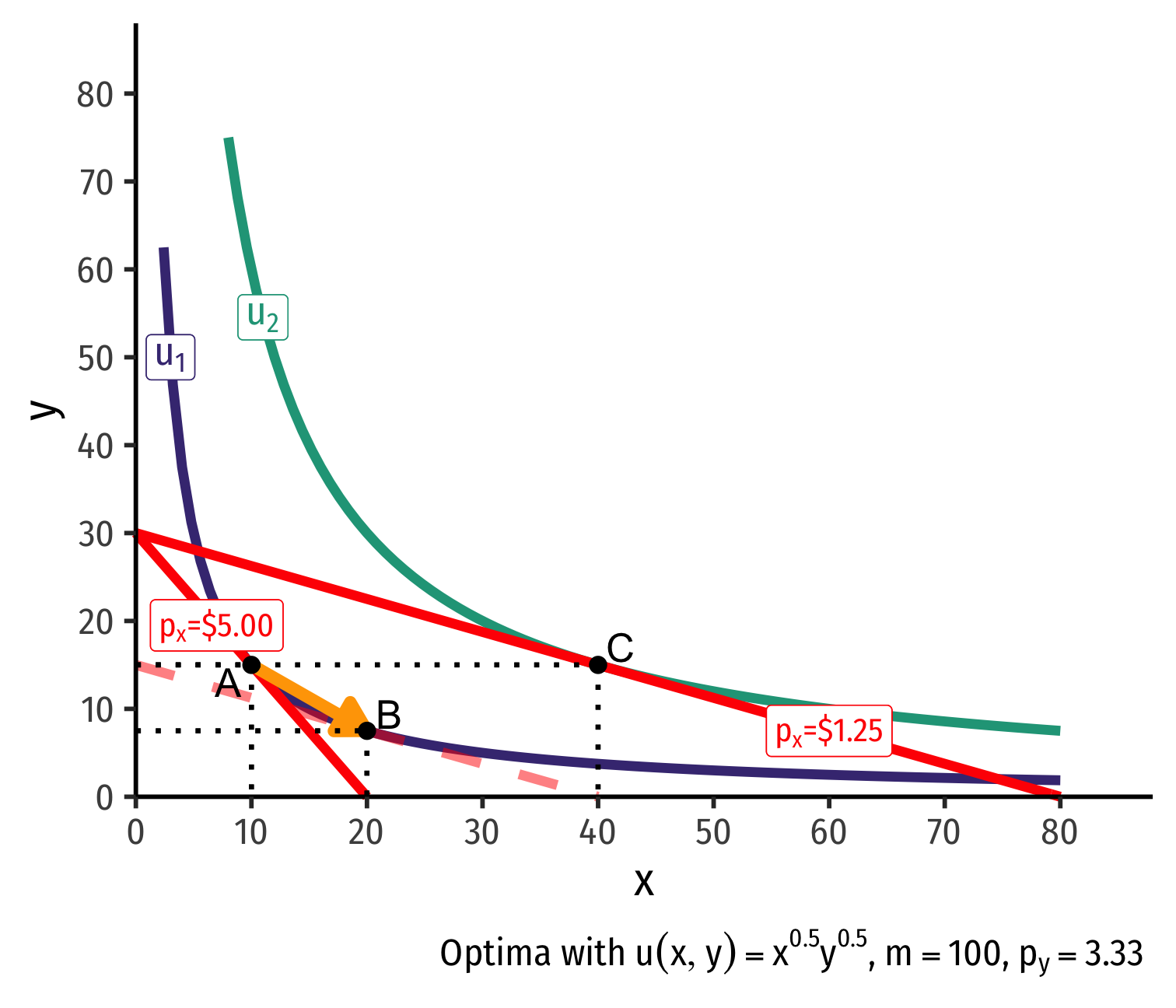
Real Income and Substitution Effects, Graphically II

  • Substitution effect: what you would choose under the new exchange rate to remain indifferent as before the change

Real Income and Substitution Effects, Graphically II

  • Substitution effect: what you would choose under the new exchange rate to remain indifferent as before the change

  • Graphically: shift new budget constraint inwards until tangent with old indifference curve

  • A→B on same I.C. (↑ x, ↓ y)

    • Point B must be a different point on the original curve!

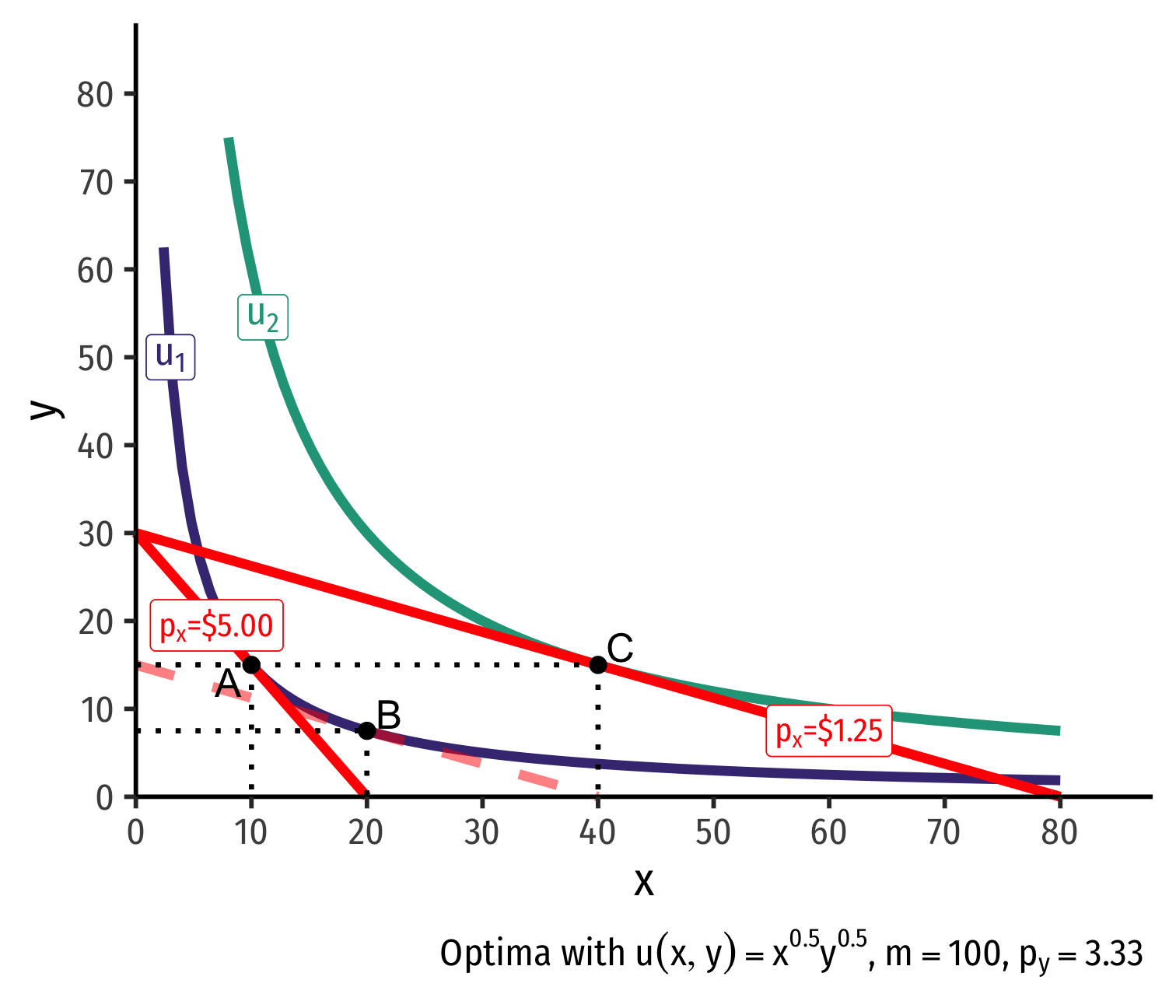
Real Income and Substitution Effects, Graphically II

  • Substitution effect: what you would choose under the new exchange rate to remain indifferent as before the change

  • Graphically: shift new budget constraint inwards until tangent with old indifference curve

  • A→B on same I.C. (↑ x, ↓ y)

    • Point B must be a different point on the original curve!

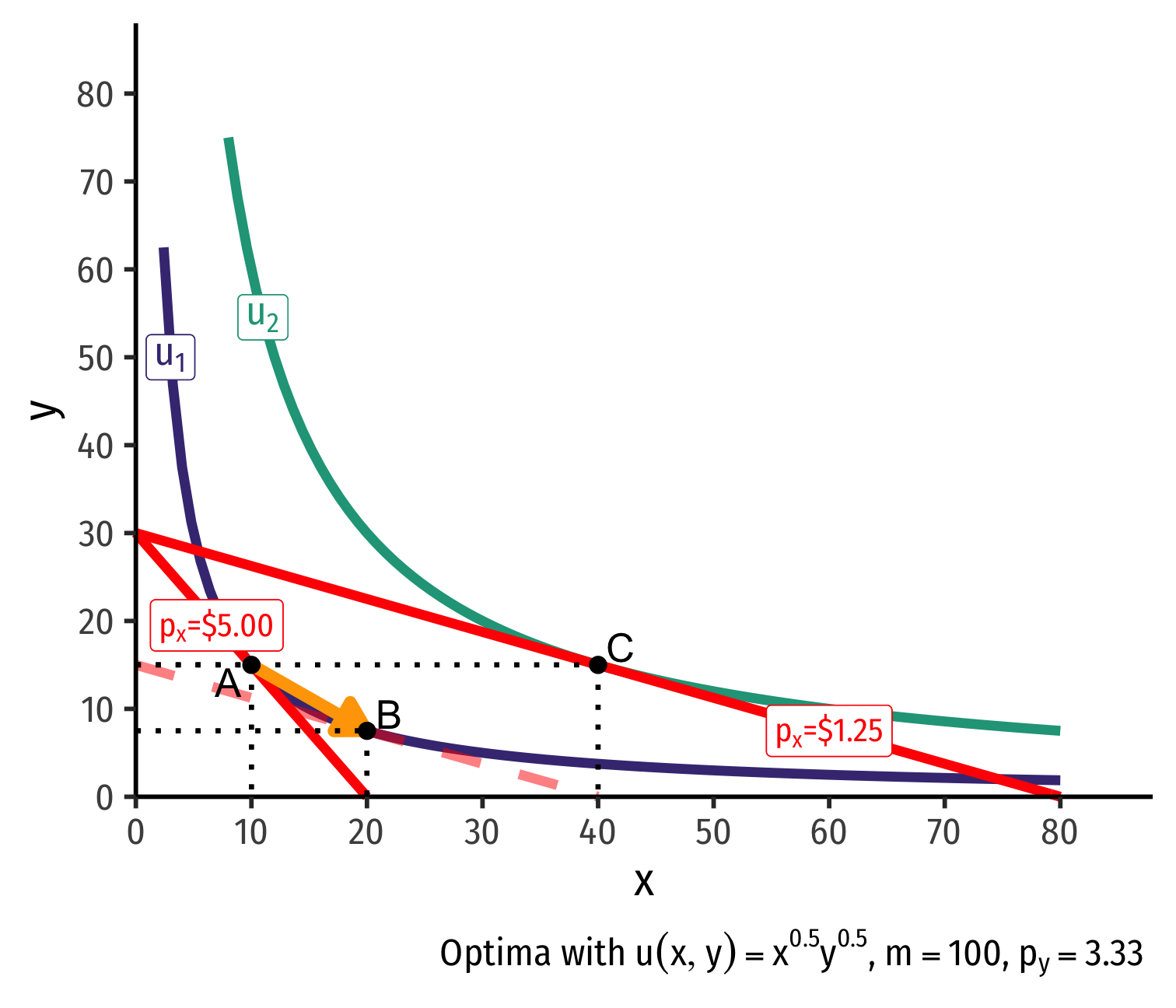
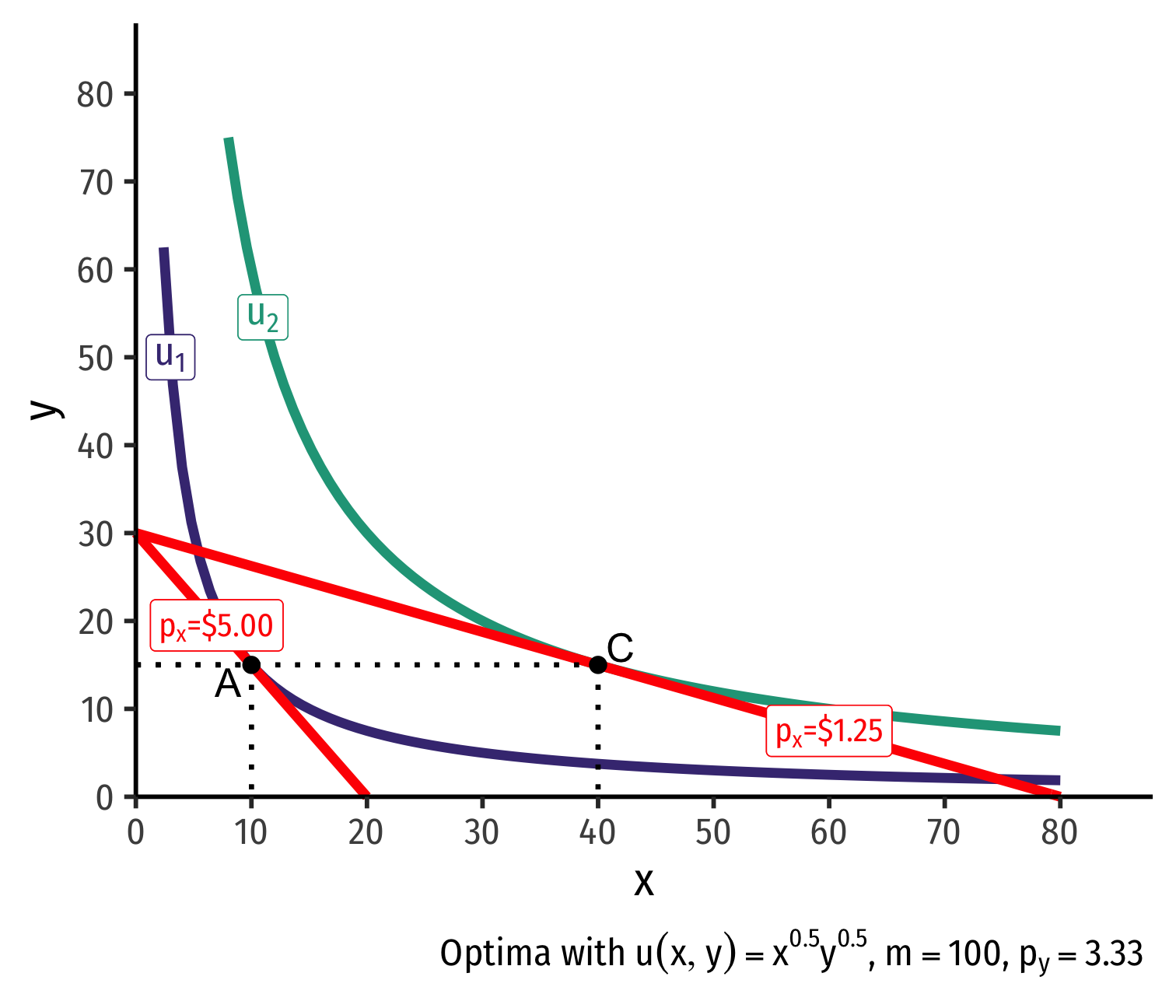
Real Income and Substitution Effects, Graphically III

  • (Real) income effect: change in consumption due to the change in purchasing power from the change in price

Real Income and Substitution Effects, Graphically III

  • (Real) income effect: change in consumption due to the change in purchasing power from the change in price

  • B→C to new budget constraint (can buy more of x and/or y)

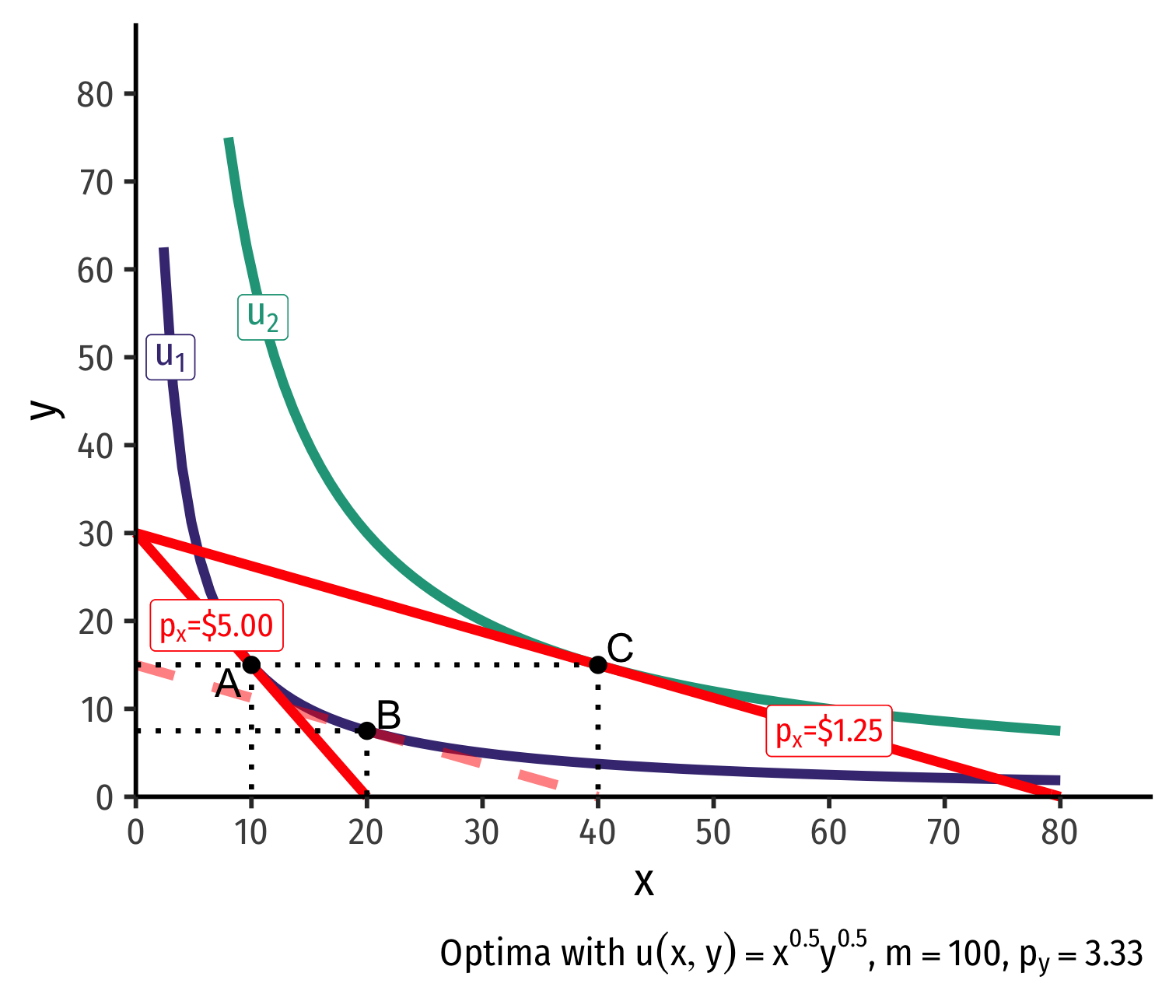
Real Income and Substitution Effects, Graphically III

  • (Real) income effect: change in consumption due to the change in purchasing power from the change in price

  • B→C to new budget constraint (can buy more of x and/or y)

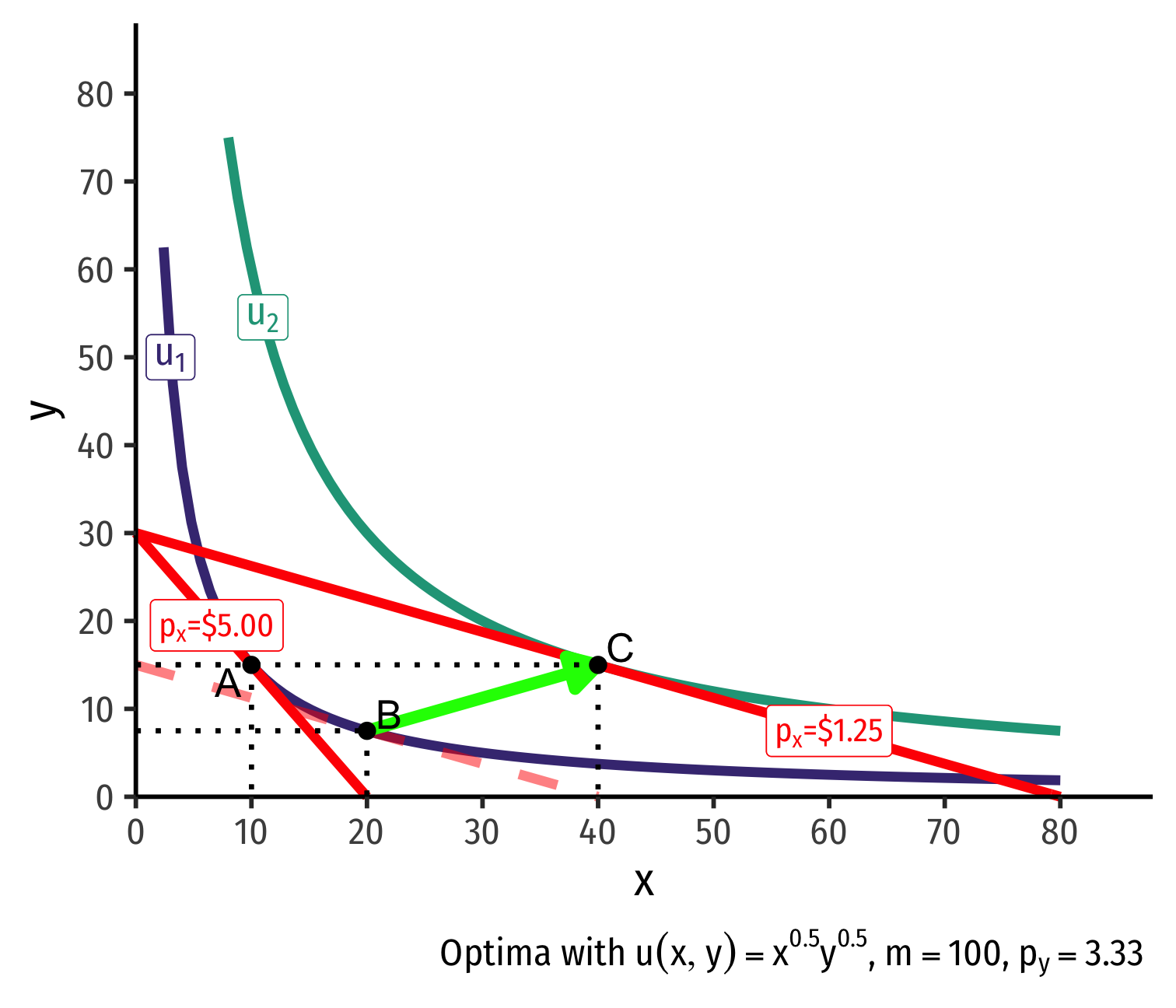
Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

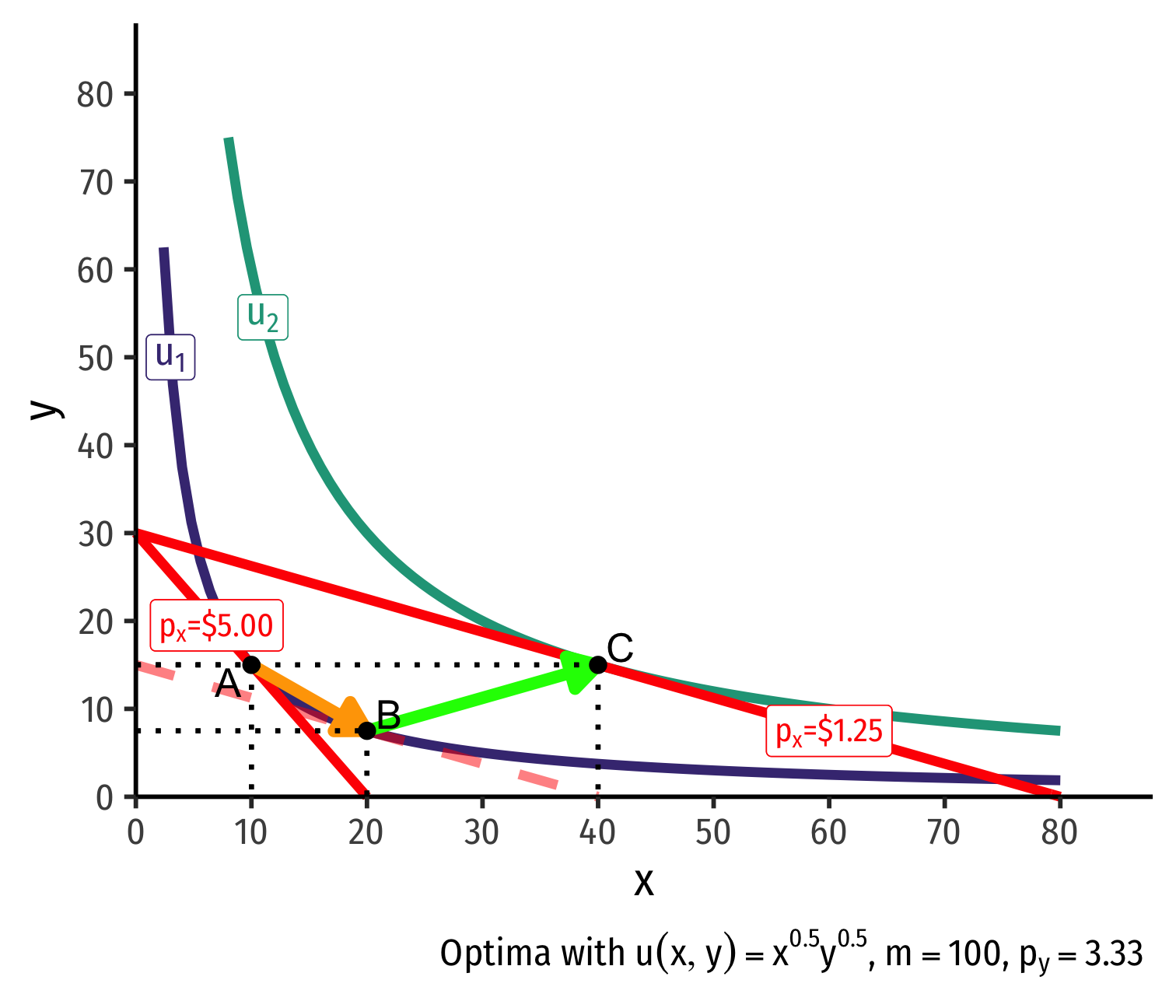
Real Income and Substitution Effects, Graphically IV

  • Original optimal consumption (A)

  • Price of x falls, new optimal consumption at (C)

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y)

  • (Total) price effect: A→C

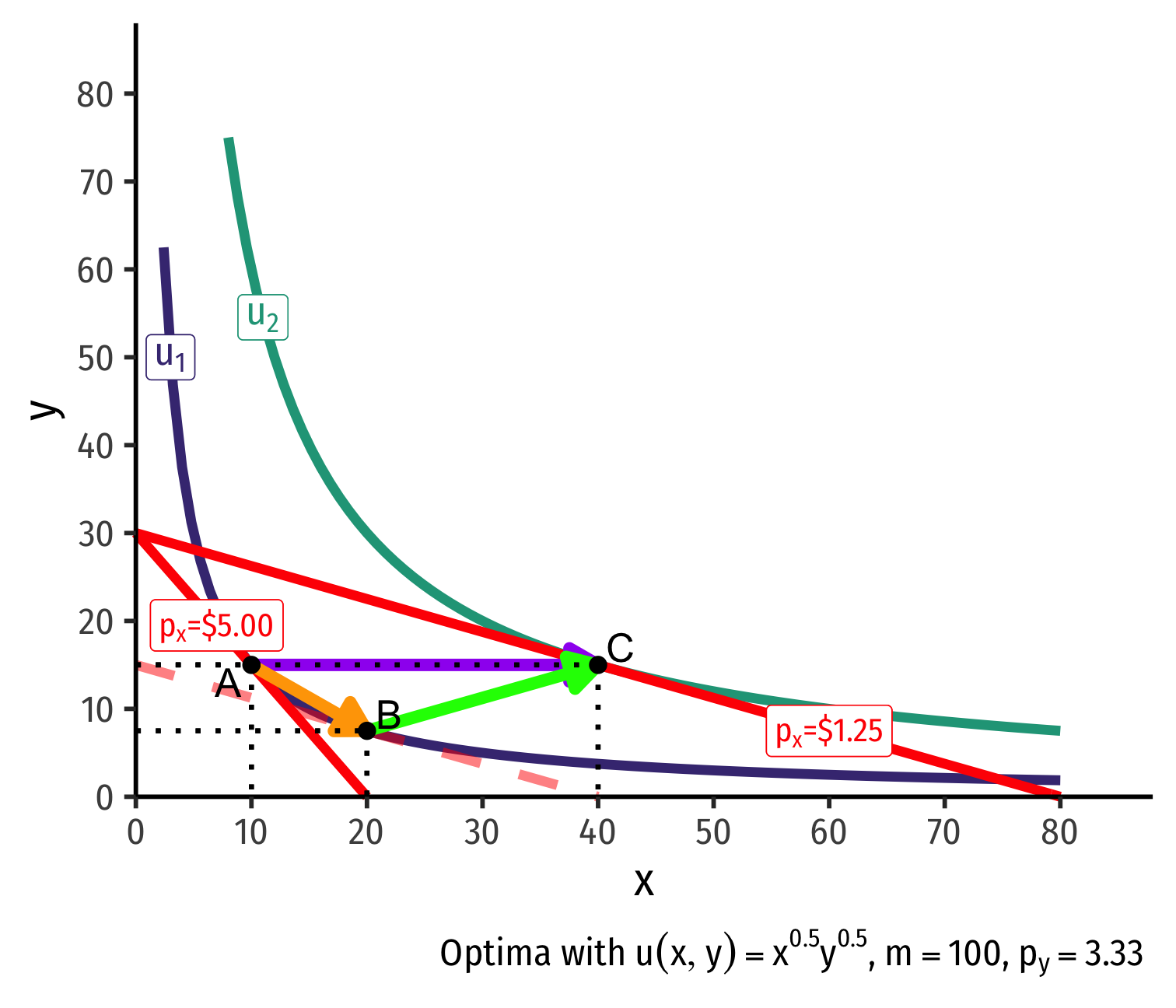
Real Income and Substitution Effects: Inferior Good

  • What about an inferior good (Ramen)?

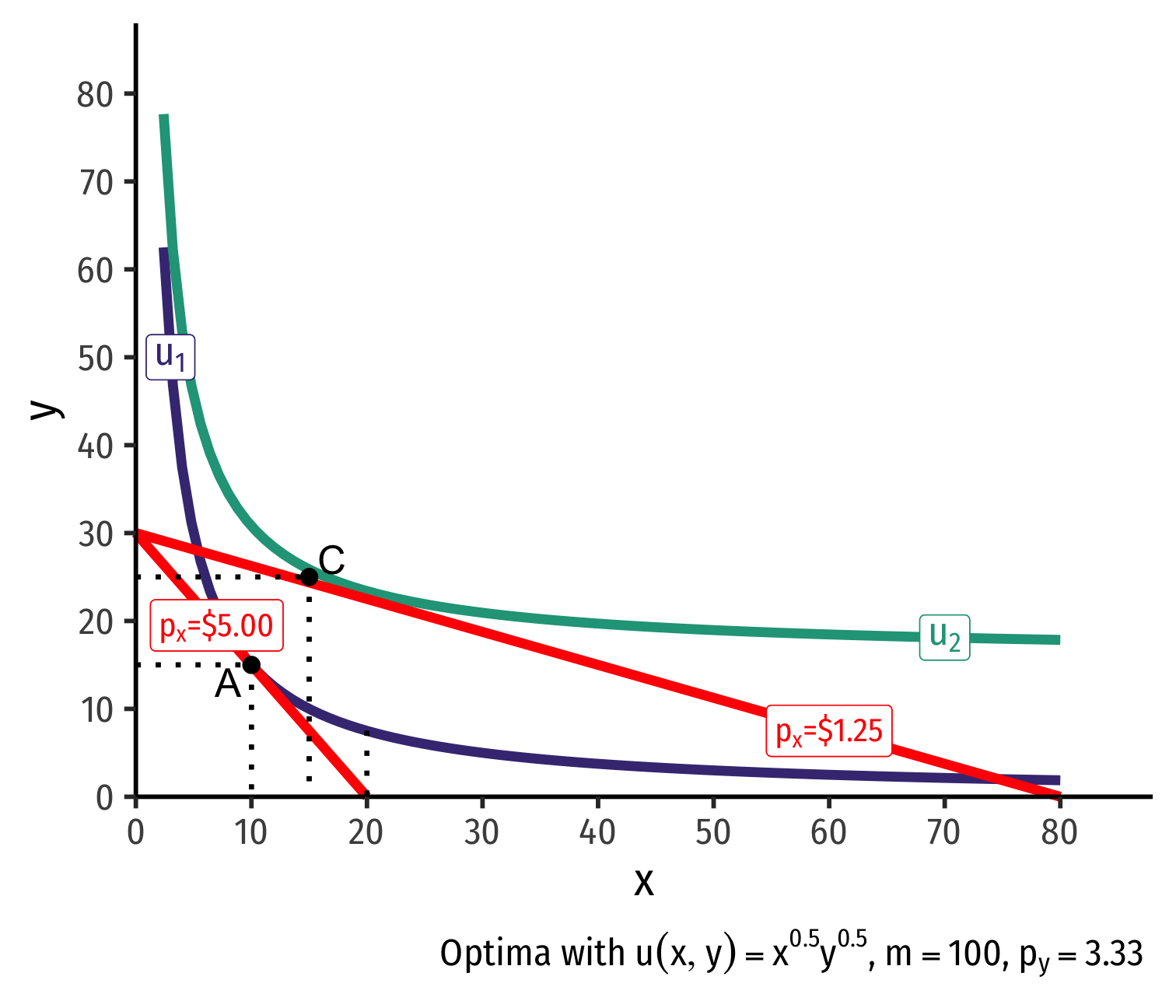
Real Income and Substitution Effects: Inferior Good

  • What about an inferior good (Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

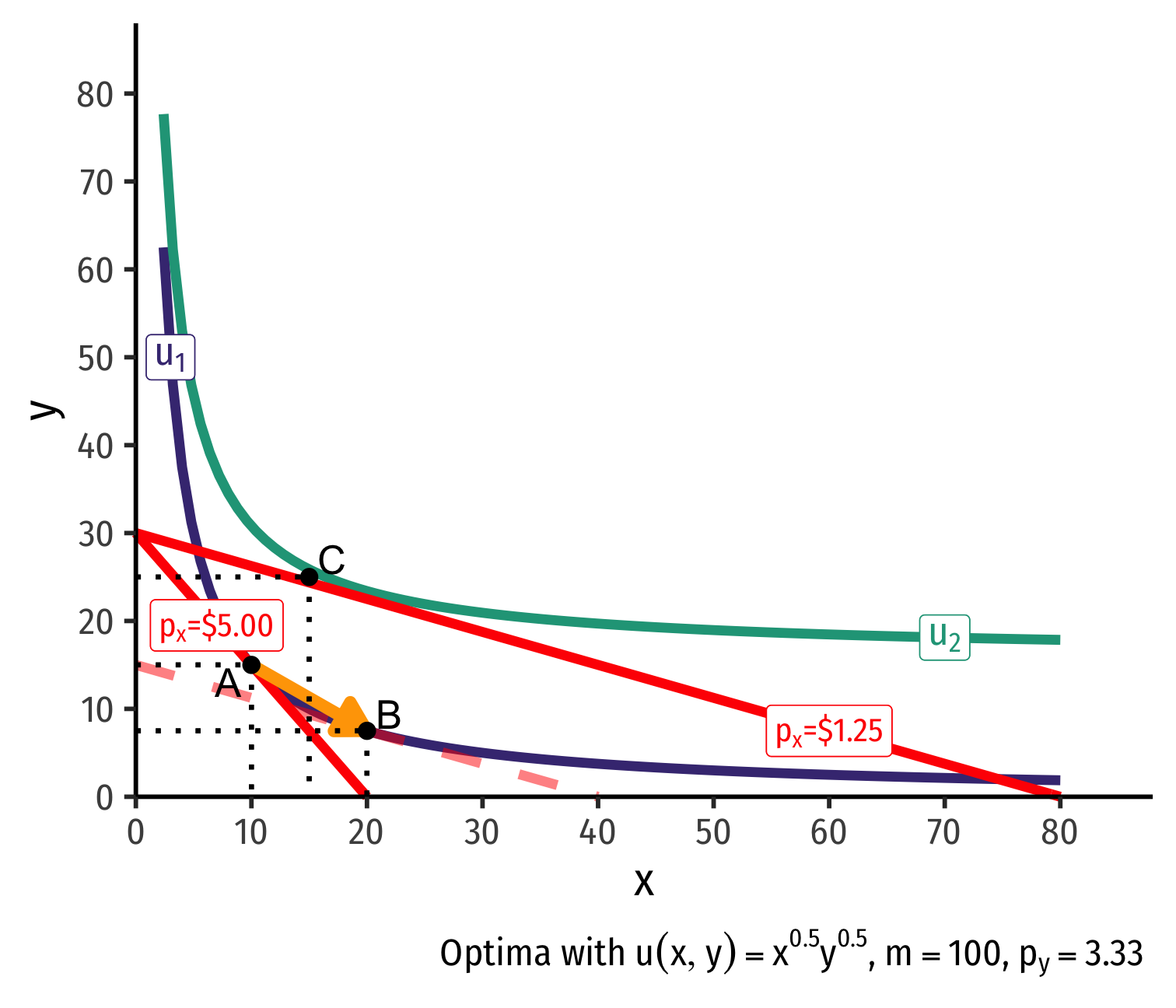
Real Income and Substitution Effects: Inferior Good

  • What about an inferior good (Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y) is negative

Real Income and Substitution Effects: Inferior Good

  • What about an inferior good (Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y) is negative

  • (Total) price effect: A→C

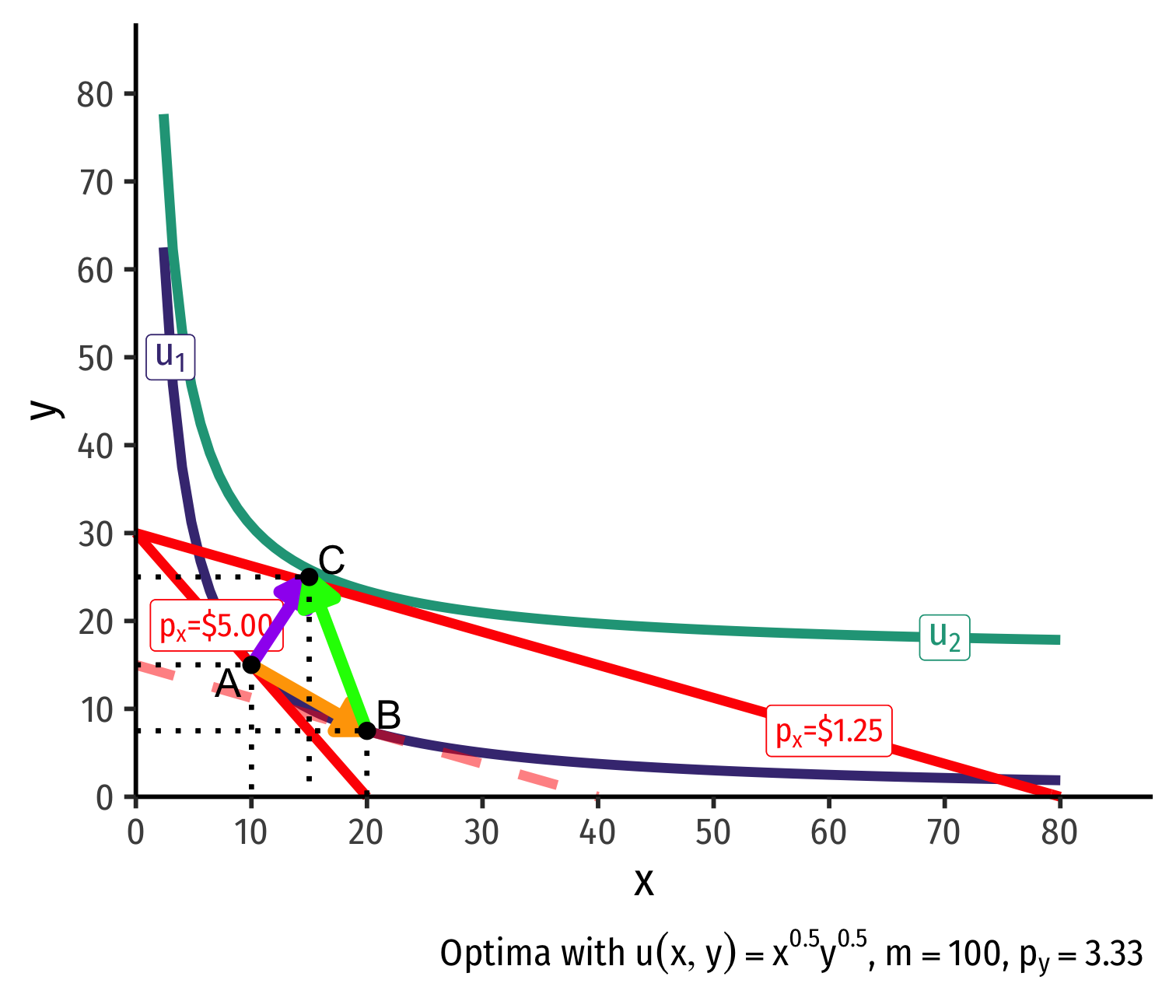
Real Income and Substitution Effects: Inferior Good

  • What about an inferior good (Ramen)?

  • Substitution effect: A→B on same I.C. (↑ cheaper x and ↓ y)

  • (Real) income effect: B→C to new budget constraint (can buy more of x and/or y) is negative

  • (Total) price effect: A→C

  • Price effect is still an ↑x from a ↓px!

    • Person would just prefer to spend more new purchasing power on other goods (y)!

  • The law of demand holds, even for inferior goods!

    • Because subst. effect dominates real income effect

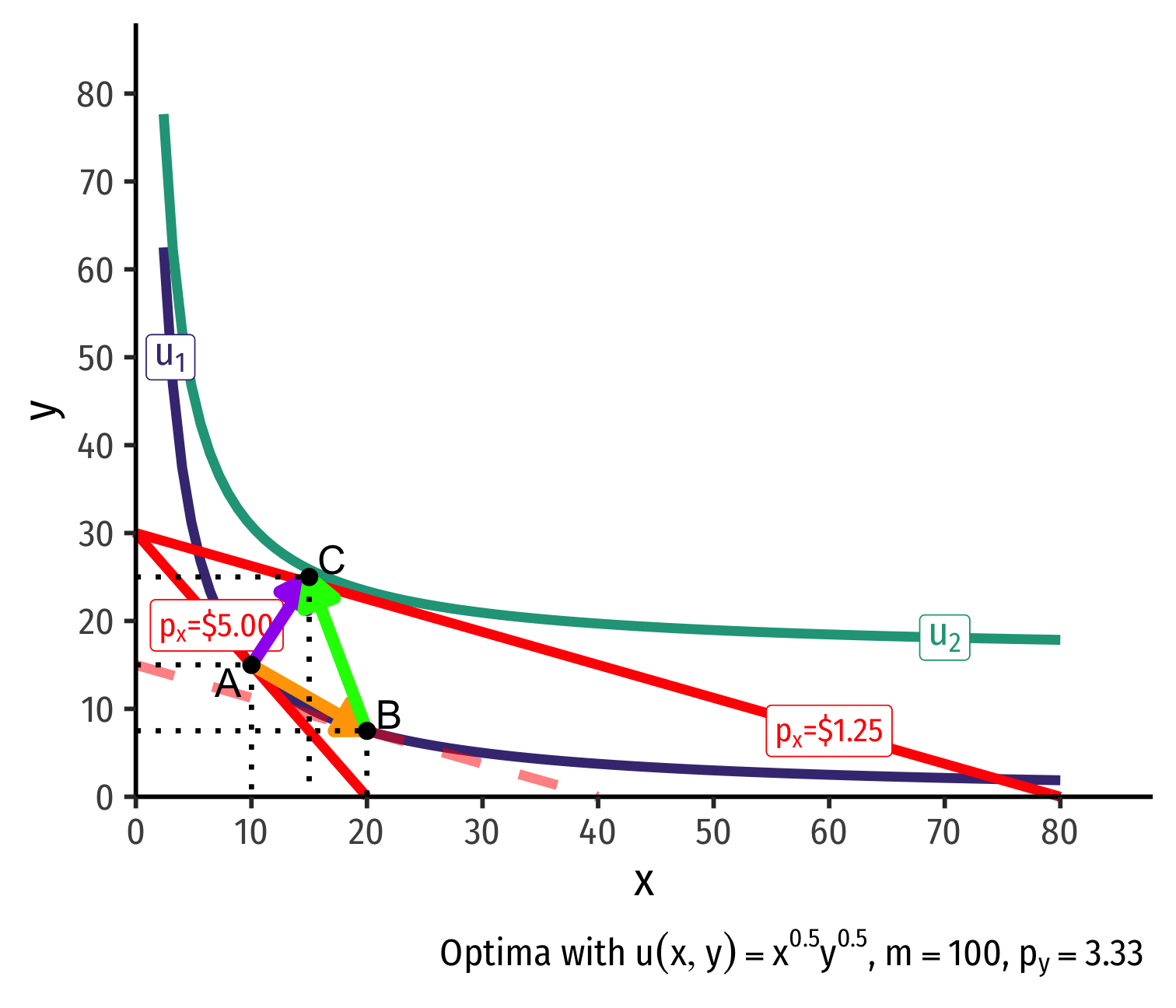
Violating the Law of Demand

Example: What would it take to violate the law of demand?

Recap: Real Income and Substitution Effects

Price Effect = Real income effect + Substitution Effect

  • Substitution effect: is always in the direction of the cheaper good

  • Real Income effect: can be positive (normal) or negative (inferior)

  • Law of Demand/Demand curves slope downwards (Price effect) mostly because of the substitution effect

    • Even (inferior) goods with negative real income effects overpowered by substitution effect

  • Exception in the theoretical Giffen good: negative R.I.E. > S.E.

    • An upward sloping demand curve!

From Optimal Consumption Points to Demand

Demand Schedule

  • Demand schedule expresses the quantity of good a person would be willing to buy (qD) at any given price (px)

  • Note: each of these is a consumer's optimum at a given price!

price quantity
10 0
9 1
8 2
7 3
6 4
5 5
4 6
3 7
8 2
9 1
10 0

Demand Curve

  • Demand curve graphically represents the demand schedule

  • Also measures a person's maximum willingness to pay (WTP) for a given quantity

  • Law of Demand (price effect) ⟹ Demand curves always slope downwards

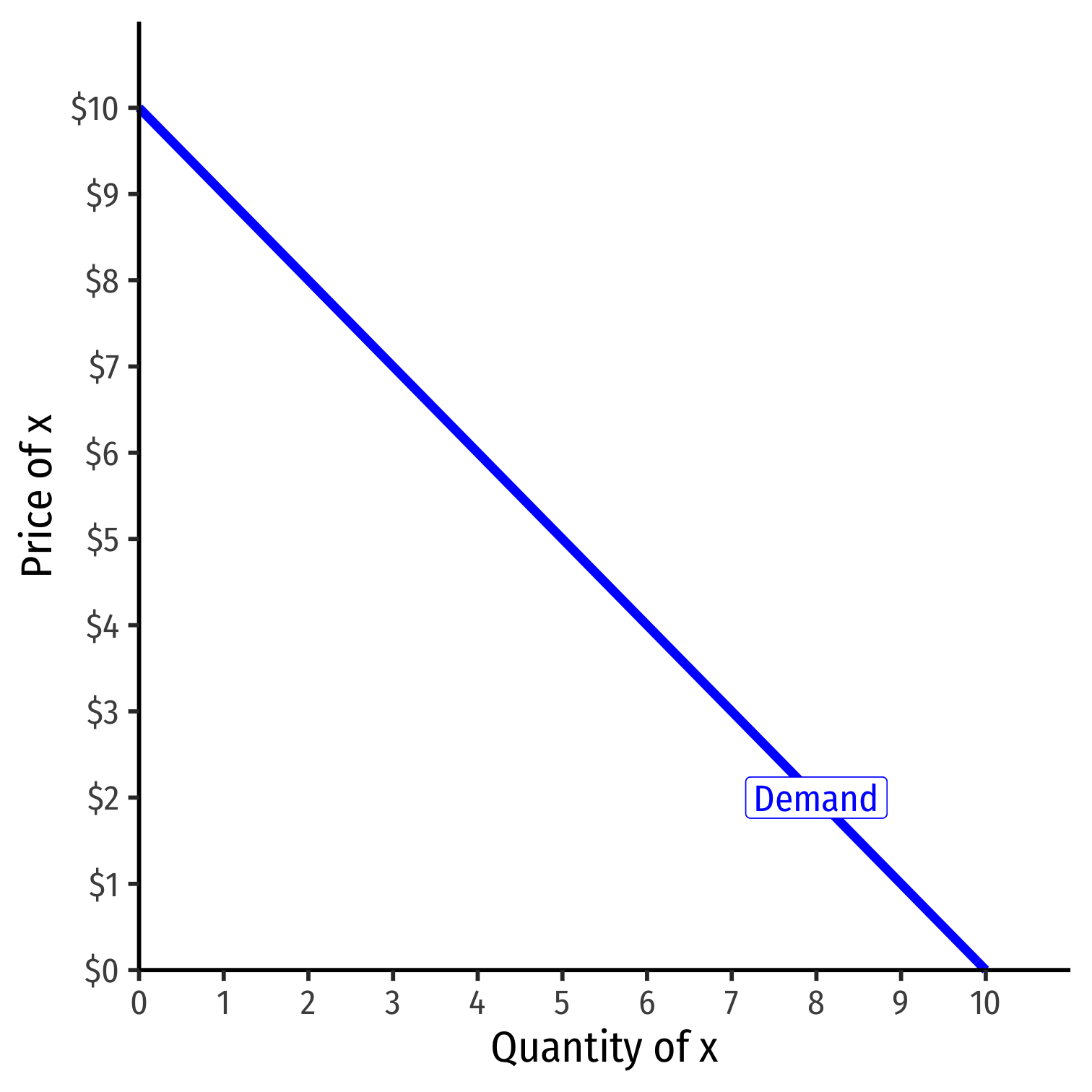
Demand Function

  • Demand function relates quantity to price

Example: q=10−p

  • Not graphable (wrong axes)!

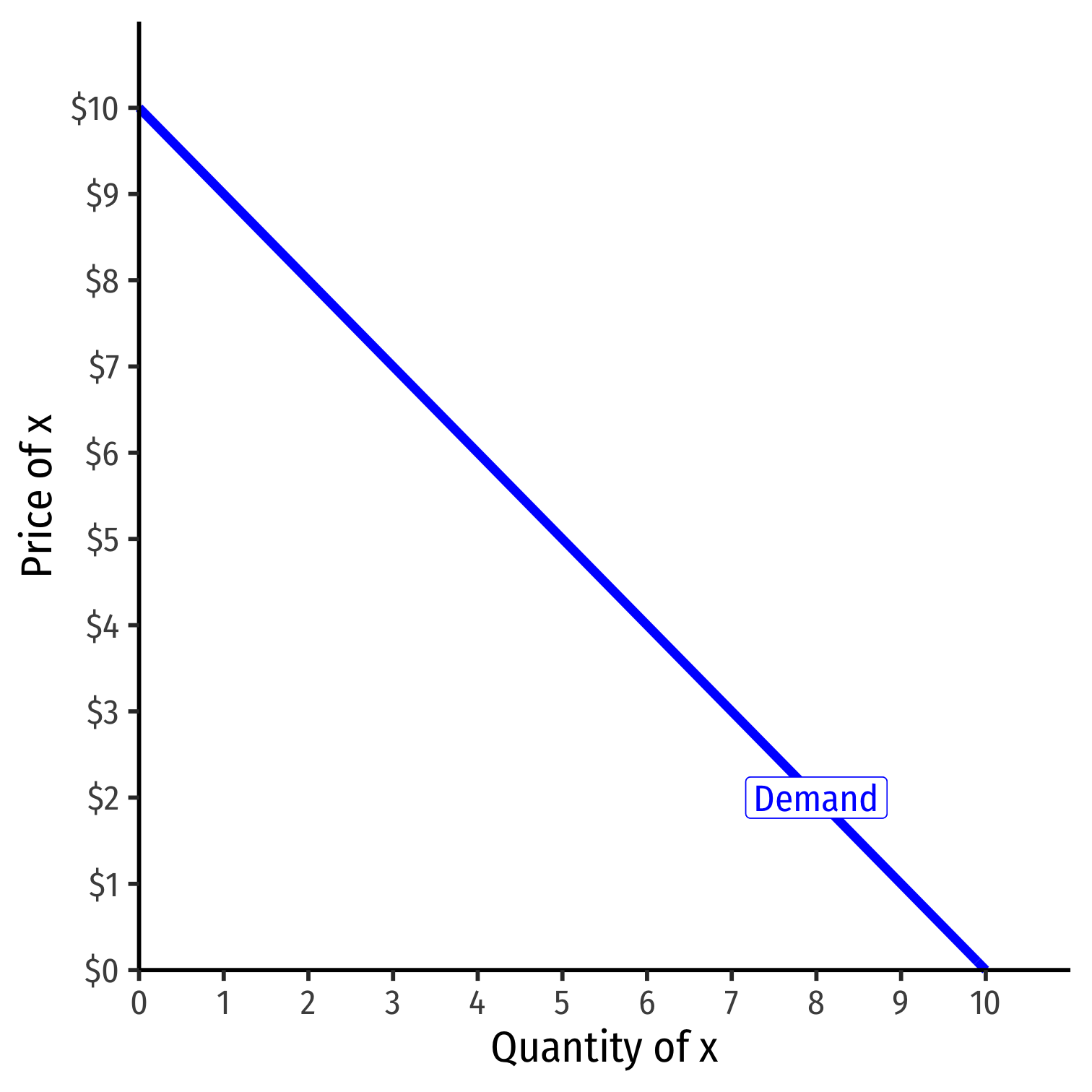
Inverse Demand Function

  • Inverse demand function relates price to quantity
    • Take demand function and solve for p

Example: p=10−q

  • Graphable (price on vertical axis)!

Inverse Demand Function

  • Inverse demand function relates price to quantity
    • Take demand function and solve for p

Example: p=10−q

  • Vertical intercept ("Choke price"): price where qD=0 ($10), just high enough to discourage any purchases

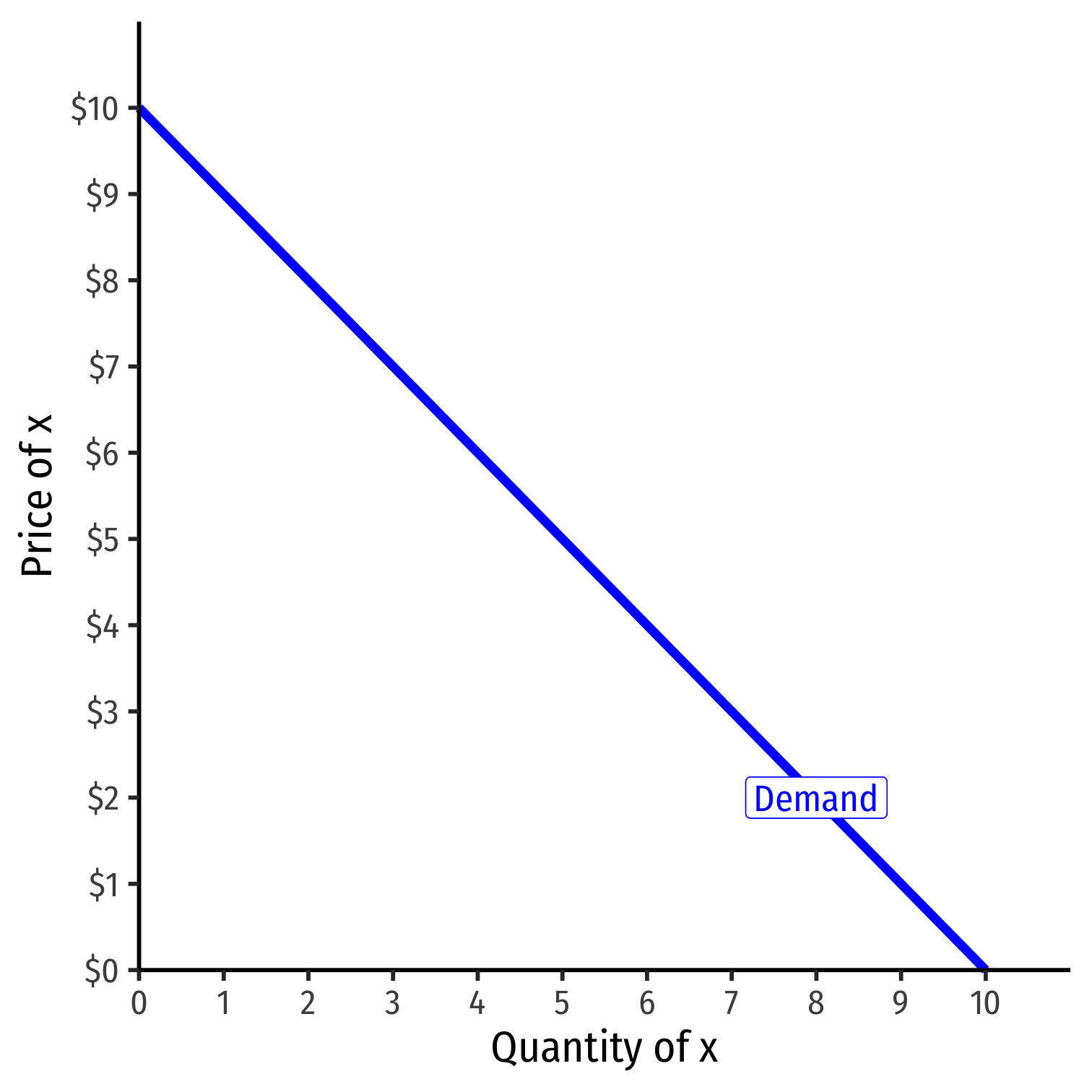
Inverse Demand Function

  • Read two ways:

  • Horizontally: at any given price, how many units person wants to buy

  • Vertically: at any given quantity, the maximum willingness to pay (WTP) for that quantity

    • This way will be very useful later

Deriving a Demand Curve Graphically

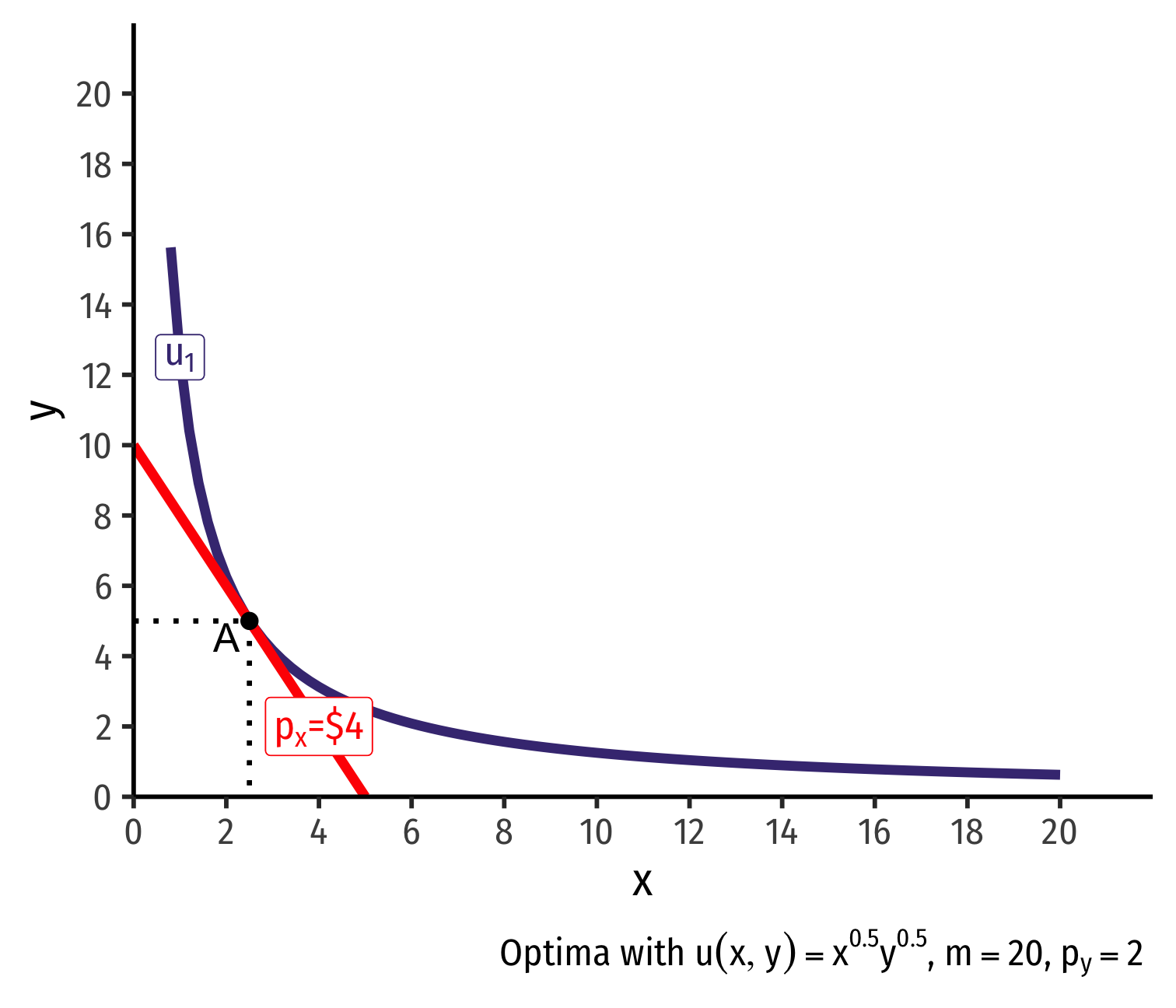
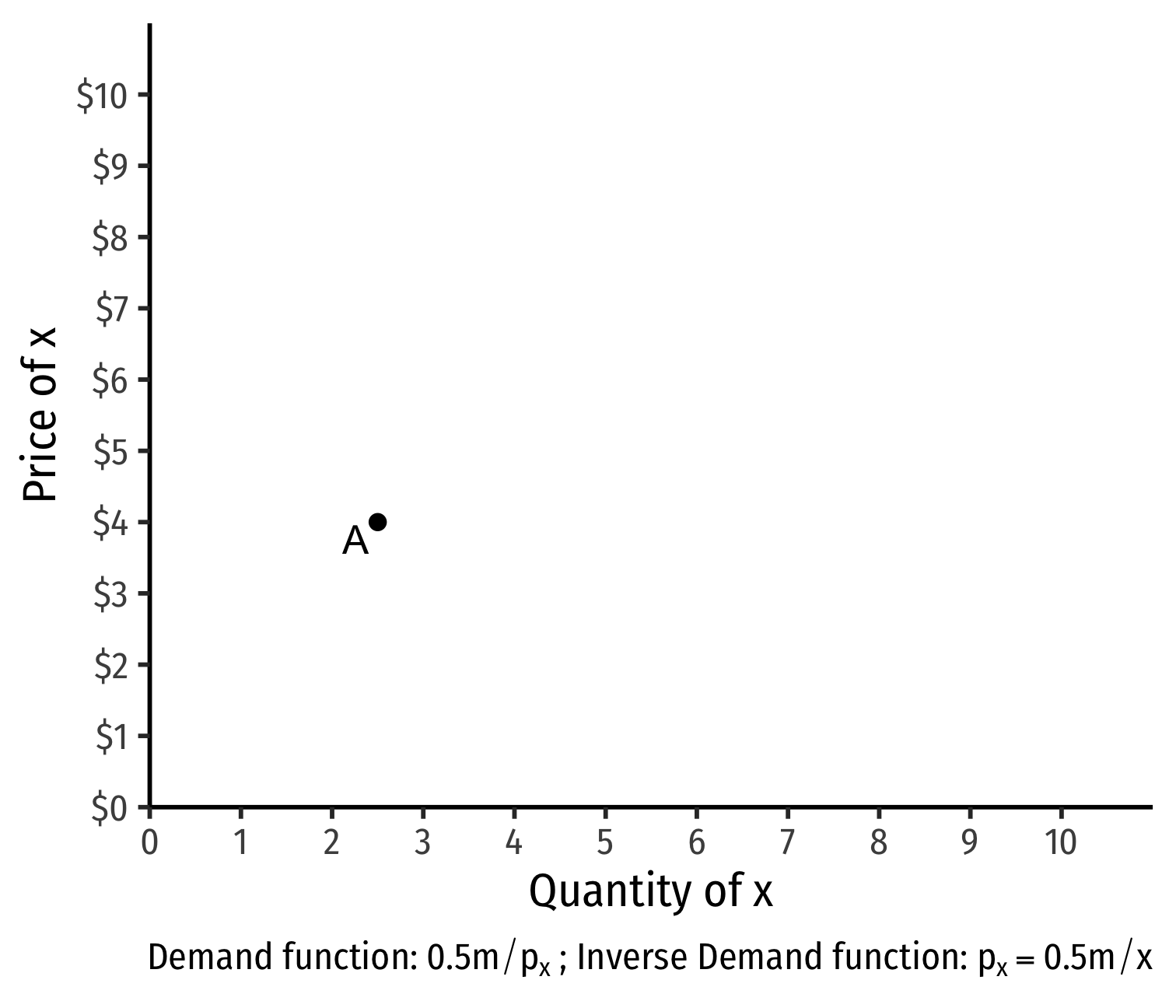
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x

Deriving a Demand Curve Graphically

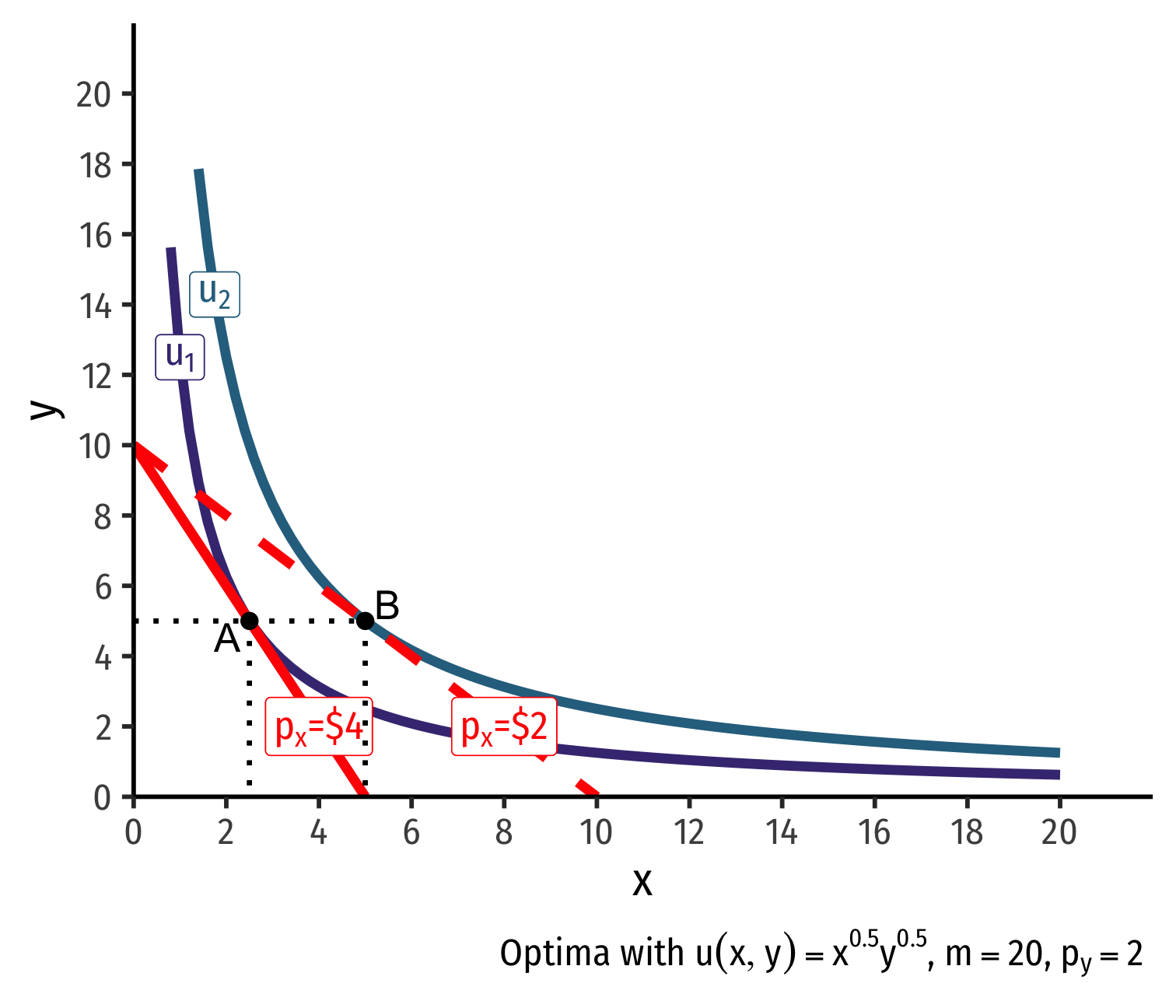
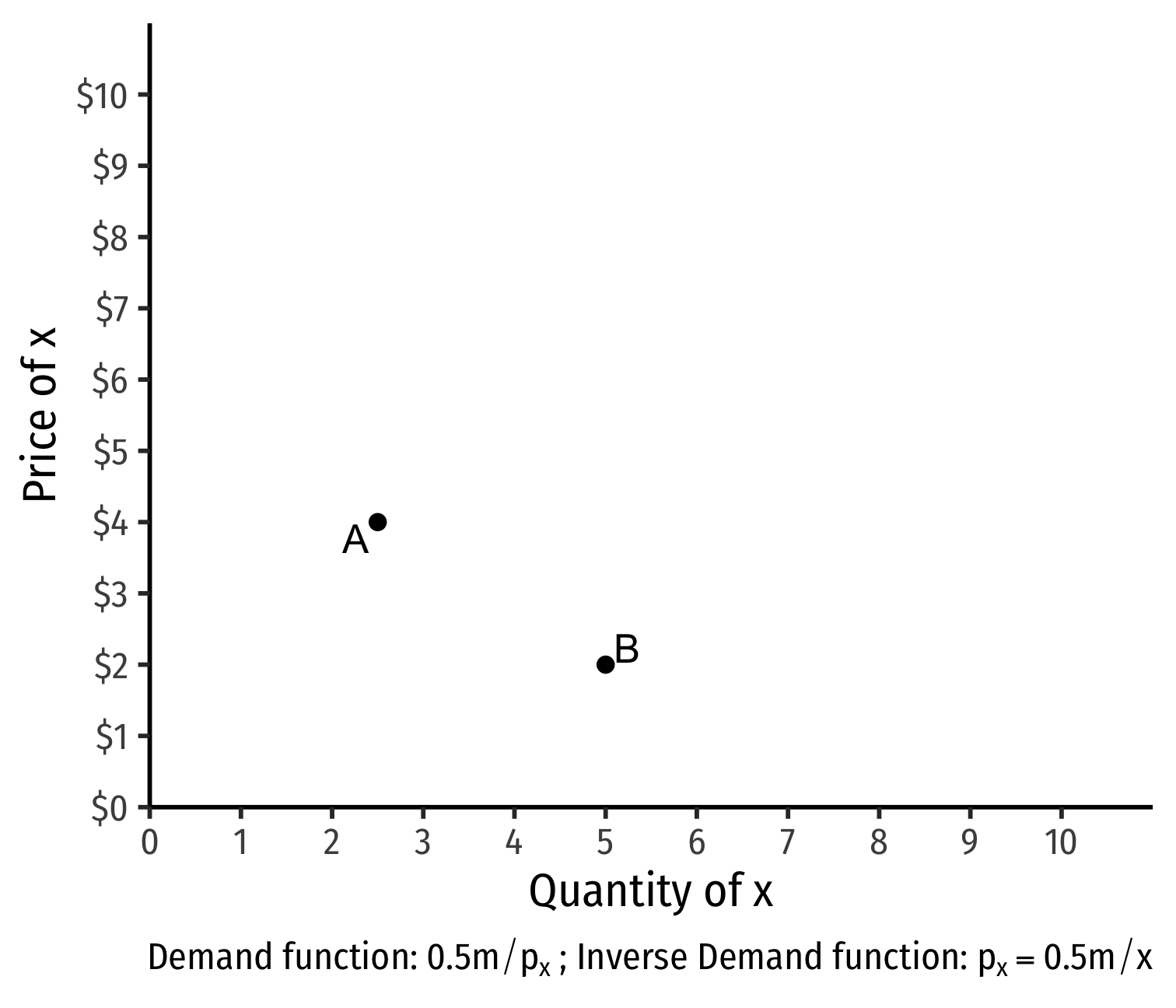
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x; at px=2, consumer buys 5 x

Deriving a Demand Curve Graphically

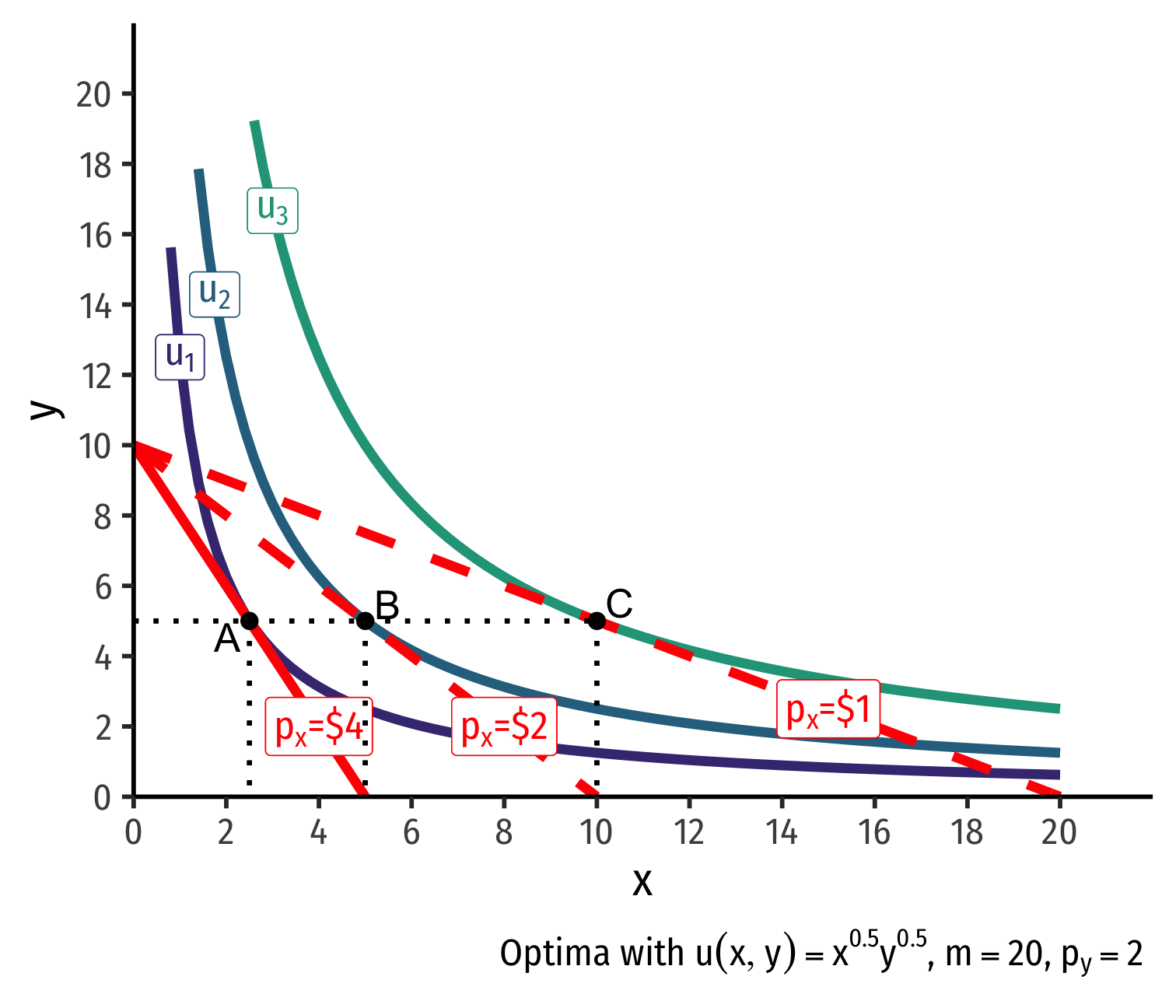
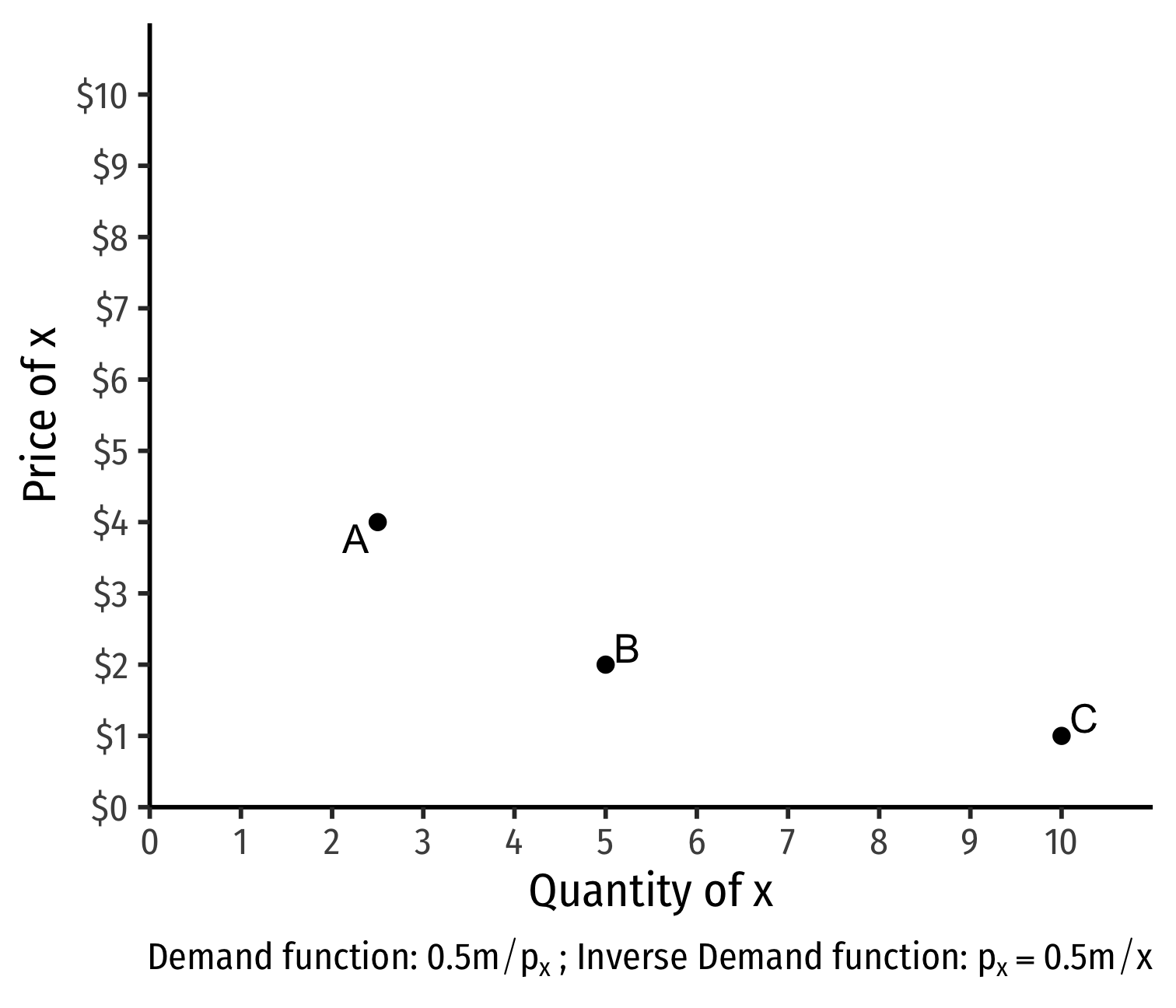
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x; at px=2, consumer buys 5 x; at px=1, consumer buys 10 x

Deriving a Demand Curve Graphically

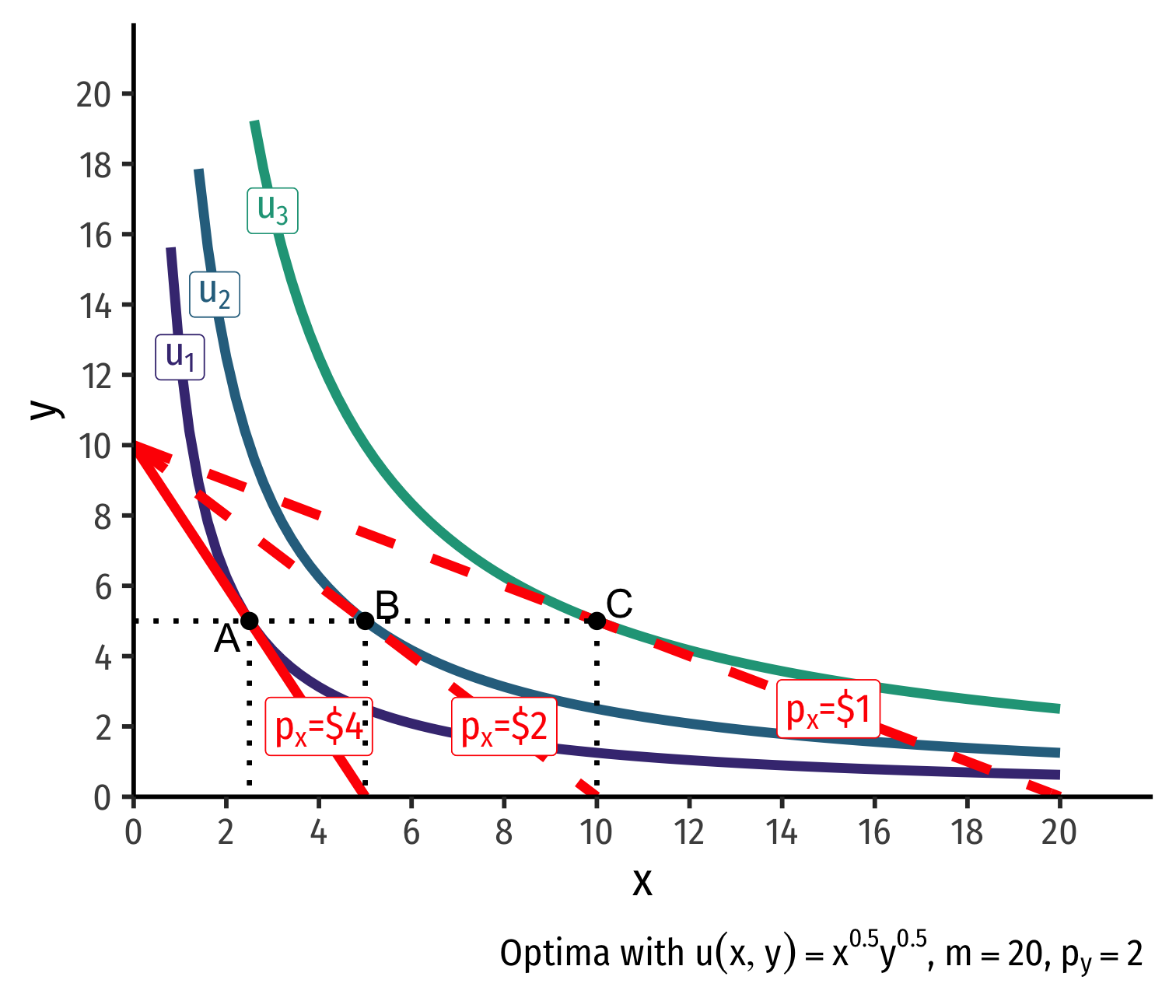
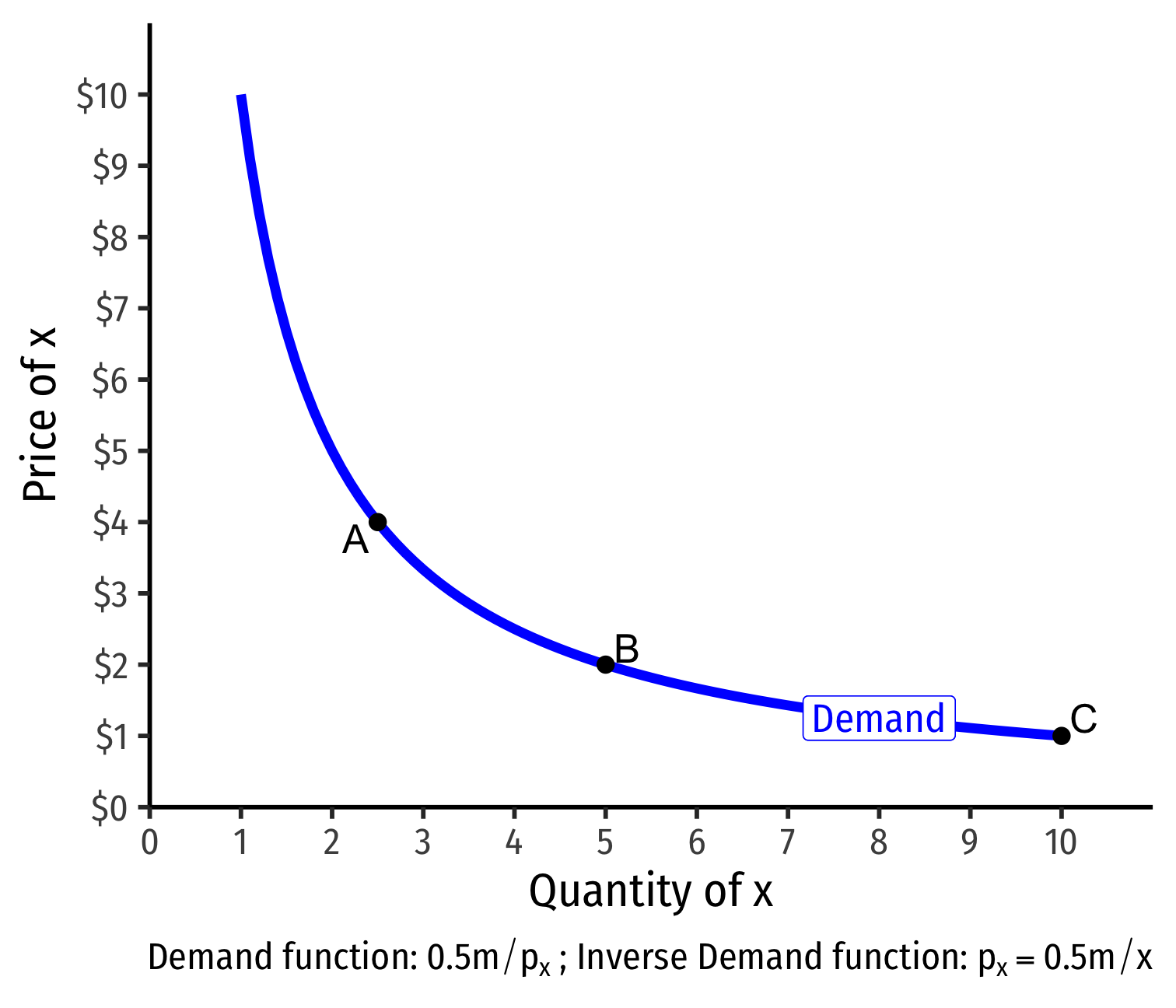
  • Demand curve for x relates consumer's optimal consumption of x ("quantity") as price of x changes
  • At px=4, consumer buys 2 x; at px=2, consumer buys 5 x; at px=1, consumer buys 10 x

Deriving a Demand Function I

  • I will always give you a (linear) demand function

  • Today's class notes page shows how you can derive actual demand functions from utility functions

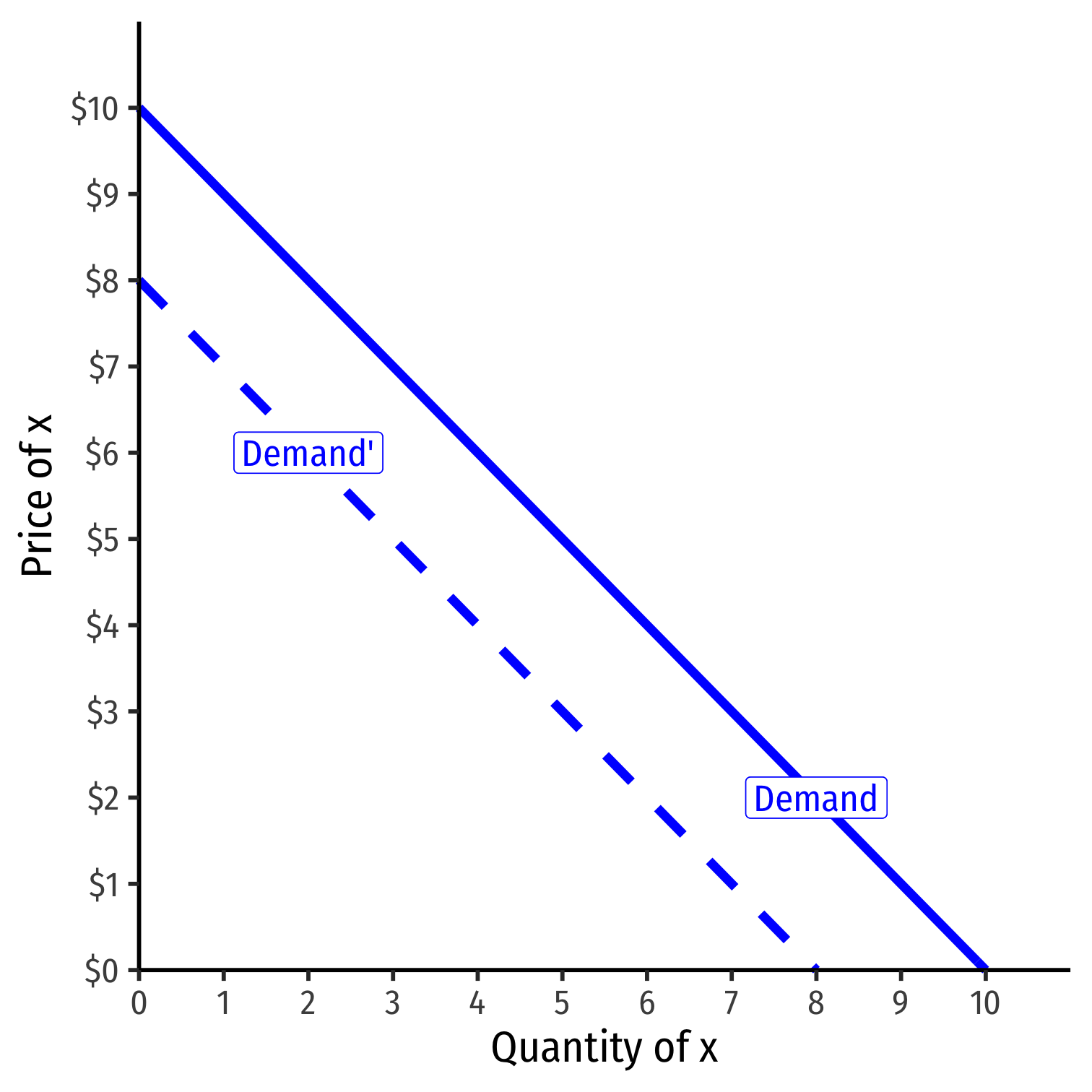
Shifts in Demand I

  • Note a simple (inverse) demand function only relates (own) price and quantity

Example: q=10−p or p=10−q

  • What about all the other "determinants of demand" like income and other prices?

  • They are captured in the vertical intercept (choke price)!

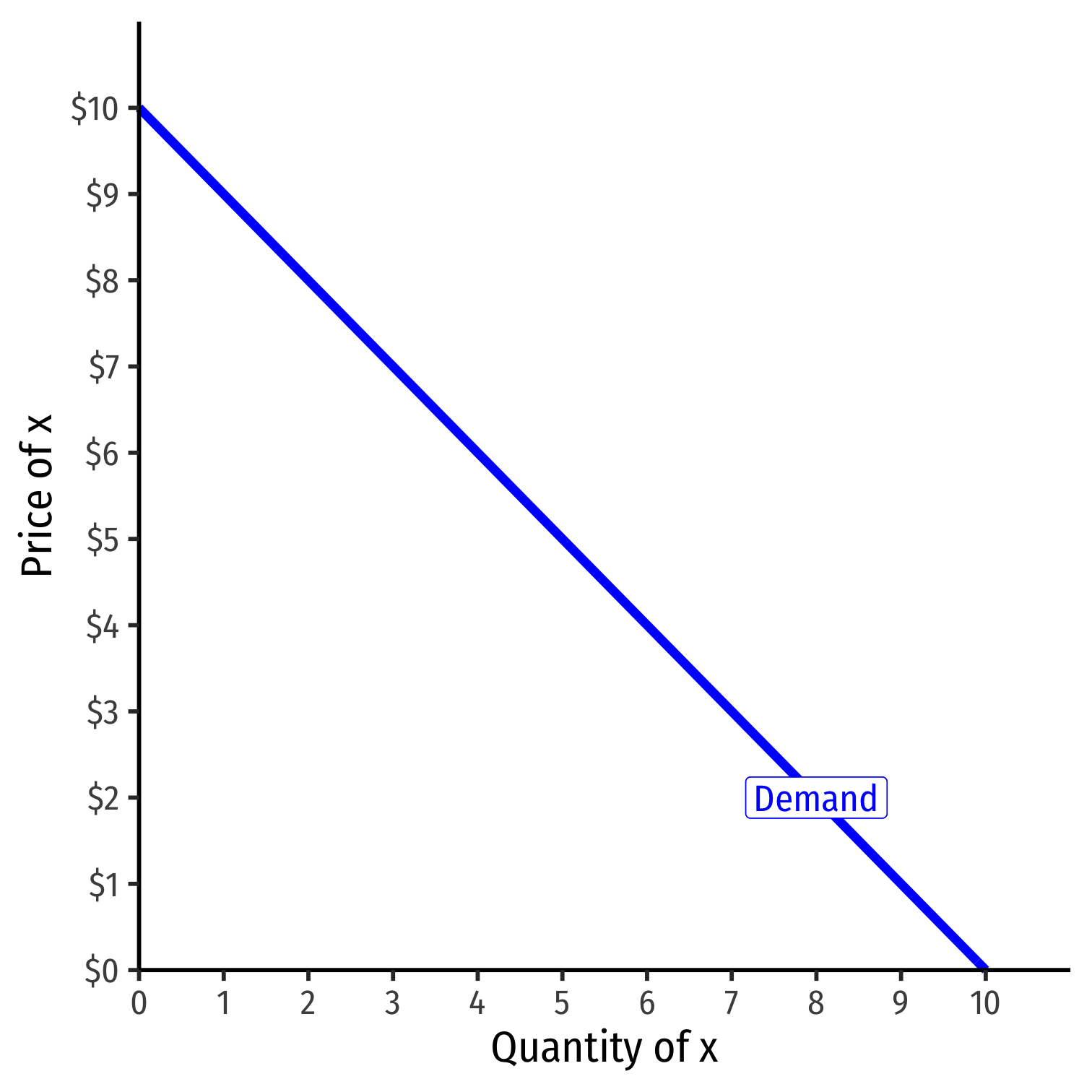
Shifts in Demand II

  • A change in one of the "determinants of demand" will shift demand curve!

    • Change in income m
    • Change in price of other goods py (substitutes or complements)
    • Change in preferences or expectations about good x
    • Change in number of buyers

  • Shows up in (inverse) demand function by a change in intercept (choke price)!

  • See my Visualizing Demand Shifters

A Demand Function (Again)

  • A consumer's demand (for good x) depends on current prices & income:

qDx=qDx(m,px,py)

  • How does demand for x change?
  1. Income effects (ΔqDxΔm): how qDx changes with changes in income
  2. Cross-price effects (ΔqDxΔpy): how qDx changes with changes in prices of other goods (e.g. y)
  3. (Own) Price effects (ΔqDxΔpx): how qDx changes with changes in price (of x)

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow