+ - 0:00:00
Notes for current slide
Notes for next slide

2.2 — Short Run and Long Run

ECON 306 · Microeconomic Analysis · Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microF20
microF20.classes.ryansafner.com

The “Runs” of Production

  • “Time”-frame usefully divided between short vs. long run analysis

  • Short run: at least one factor of production is fixed (too costly to change) q=f(ˉk,l)

    • Assume capital is fixed (i.e. number of factories, storefronts, etc)
    • Short-run decisions only about using labor

The "Runs" of Production

  • "Time"-frame usefully divided between short vs. long run analysis

  • Long run: all factors of production are variable (can be changed) q=f(k,l)

Production in the Short Run

Production in the Short Run: Example

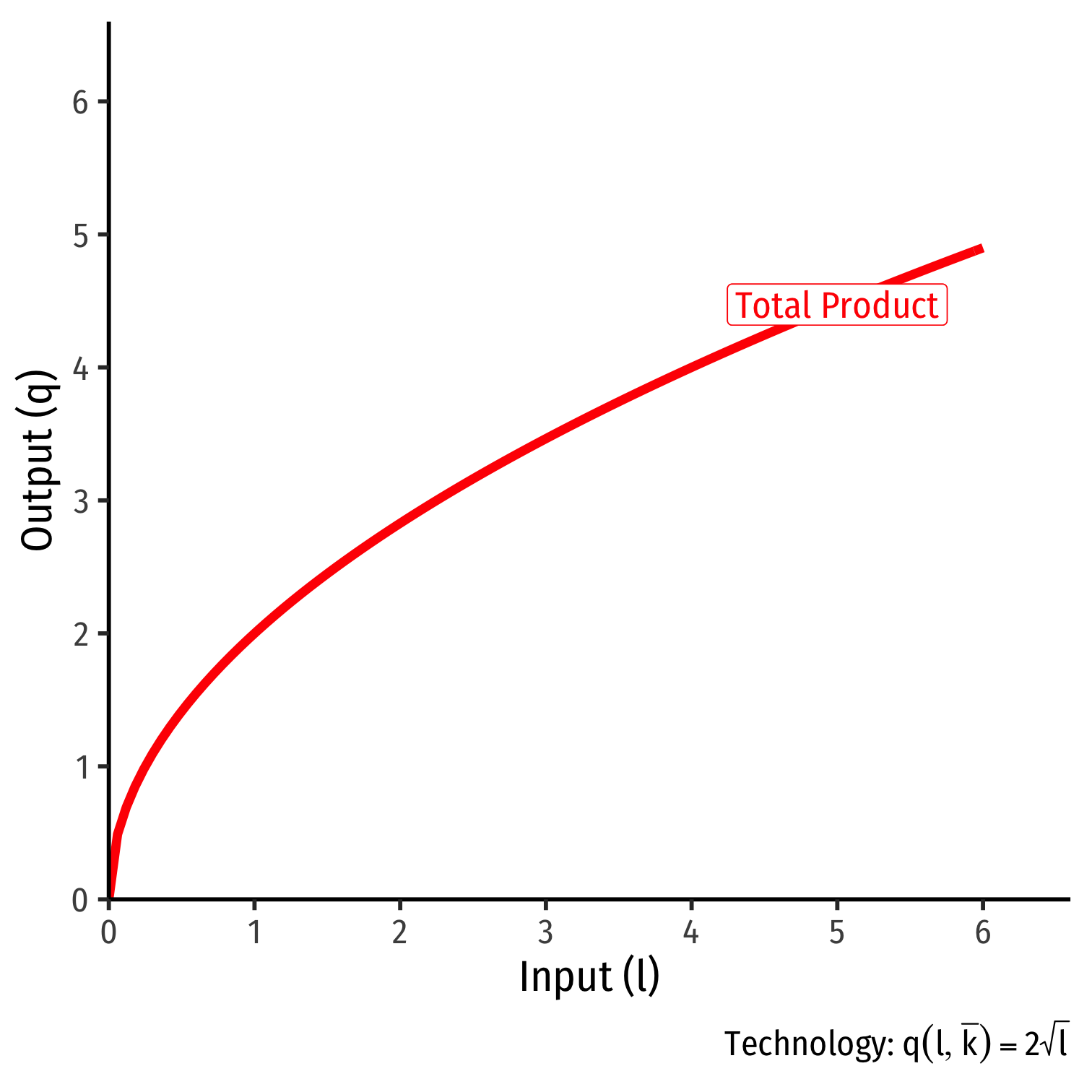
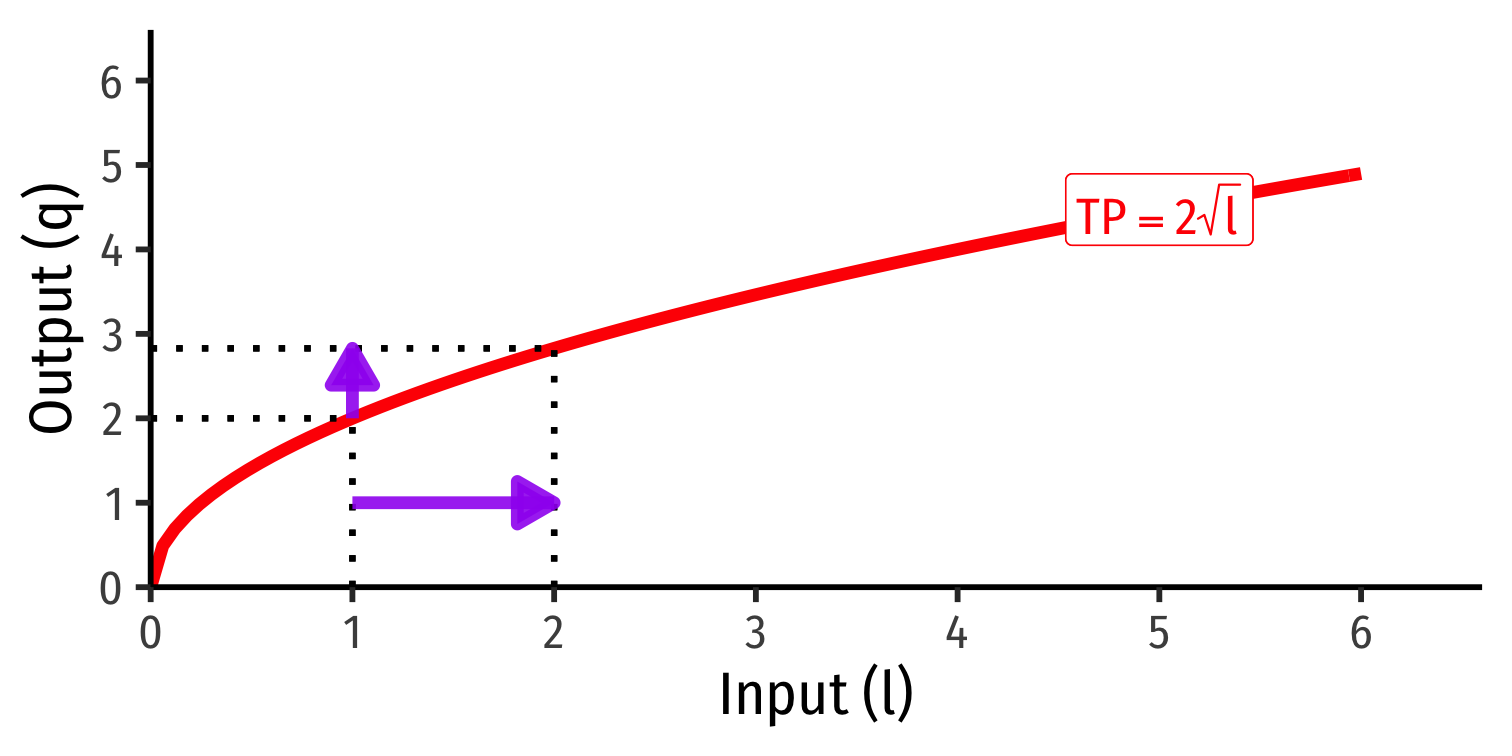
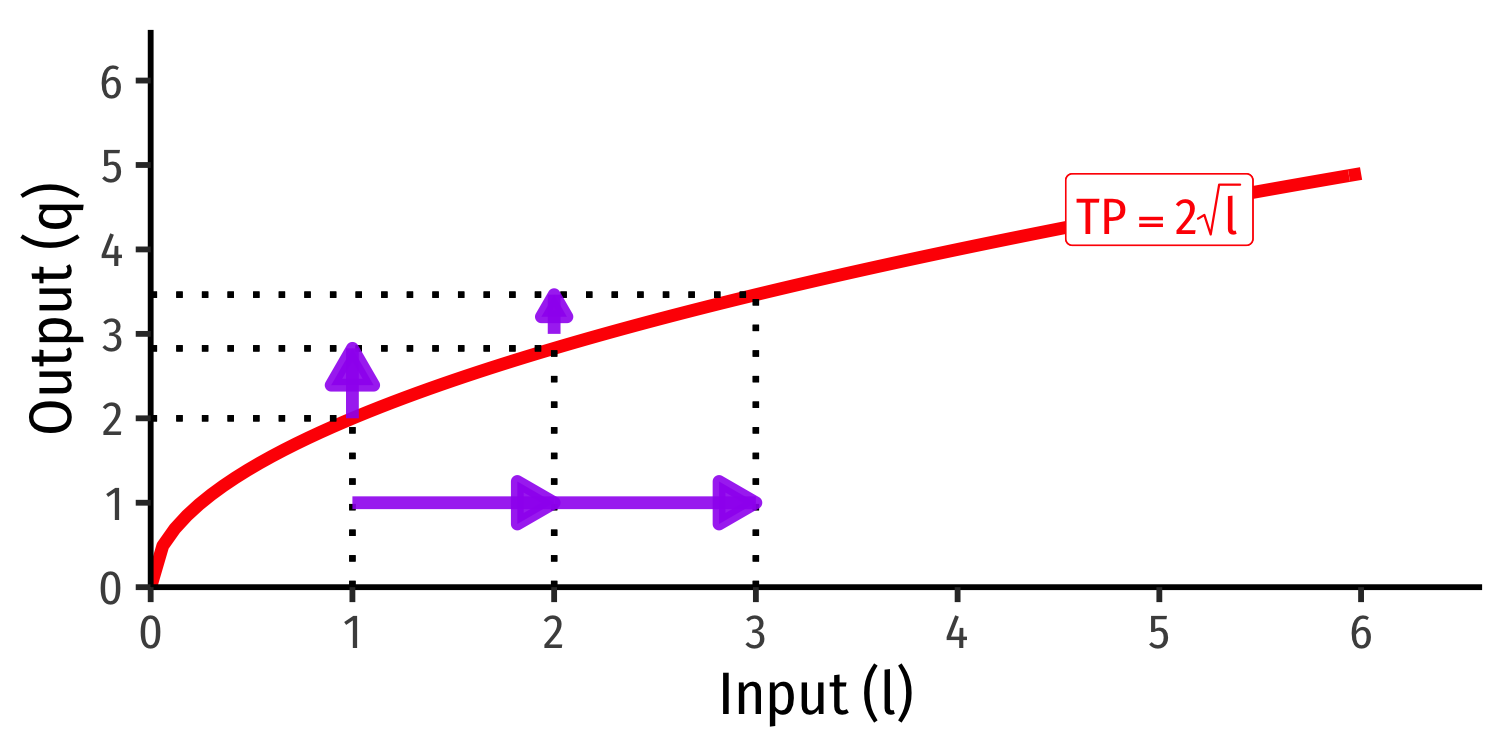
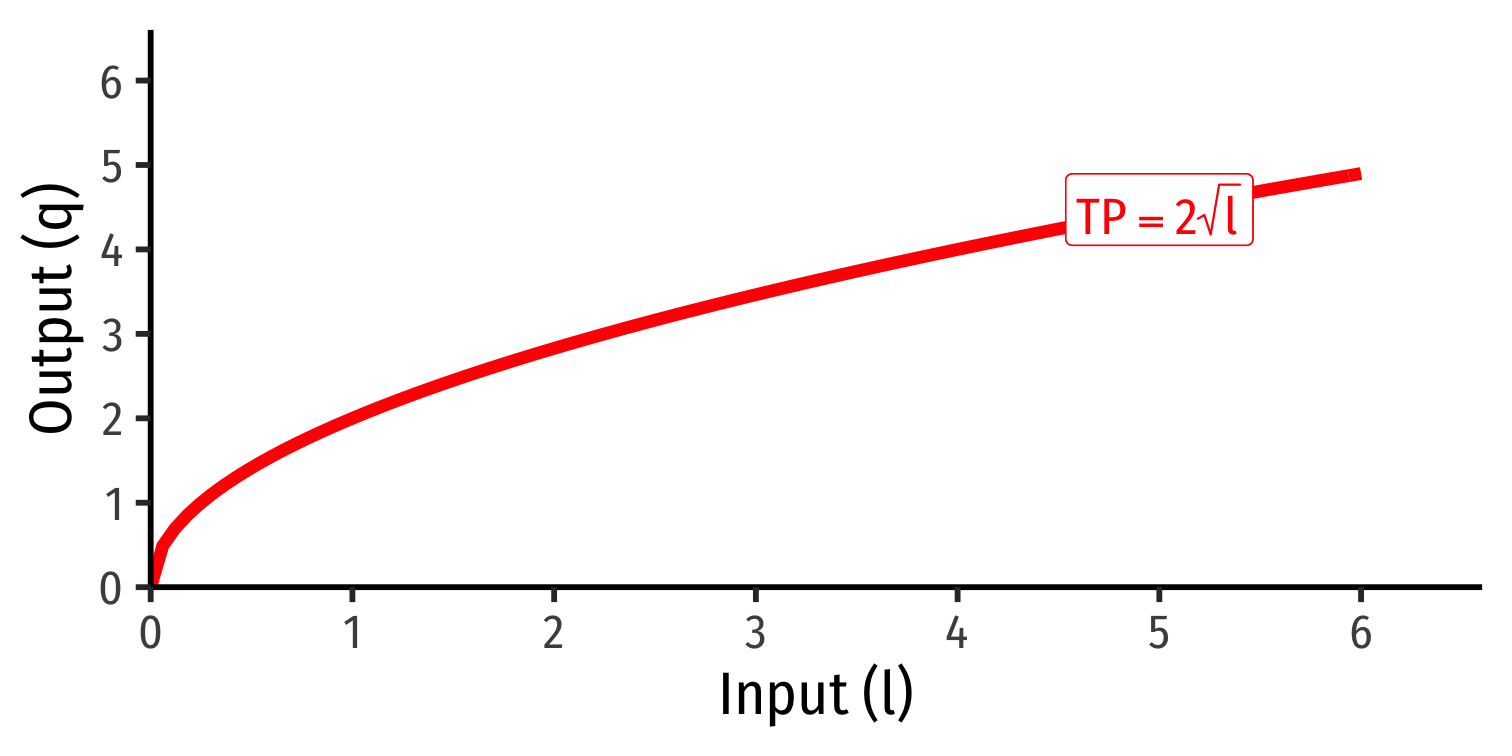
Example: Consider a firm with the production function q=k0.5l0.5

  • Suppose in the short run, the firm has 4 units of capital.
  1. Derive the short run production function.
  2. What is the total product (output) that can be made with 4 workers?
  3. What is the total product (output) that can be made with 5 workers?

Production in the Short Run: Example

Example: Consider a firm with the production function q=k0.5l0.5

  • Suppose in the short run, the firm has 4 units of capital.
  1. Derive the short run production function.
  2. What is the total product (output) that can be made with 4 workers?
  3. What is the total product (output) that can be made with 5 workers?

Marginal Products

  • The marginal product of an input is the additional output produced by one more unit of that input (holding all other inputs constant)

  • Like marginal utility

  • Similar to marginal utilities, I will give you the marginal product equations

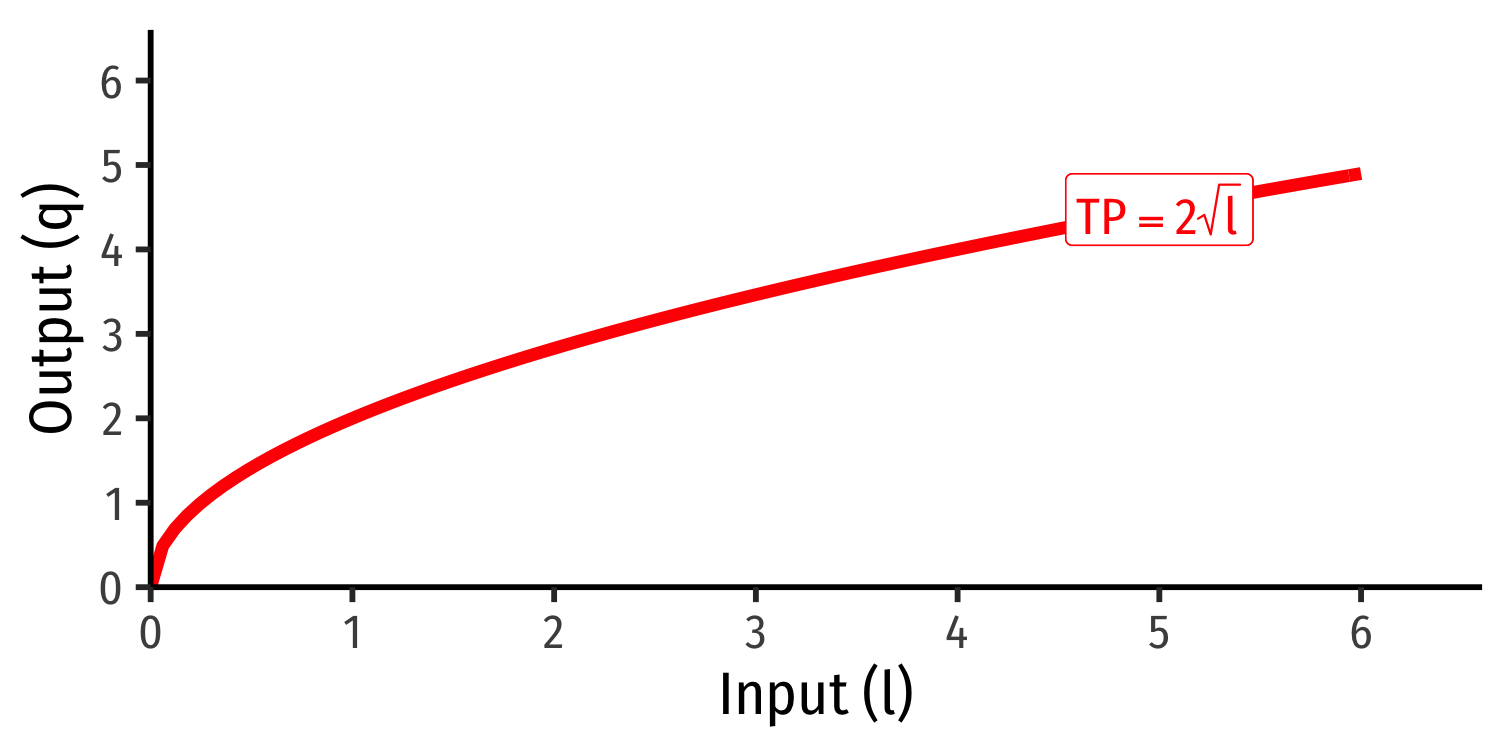
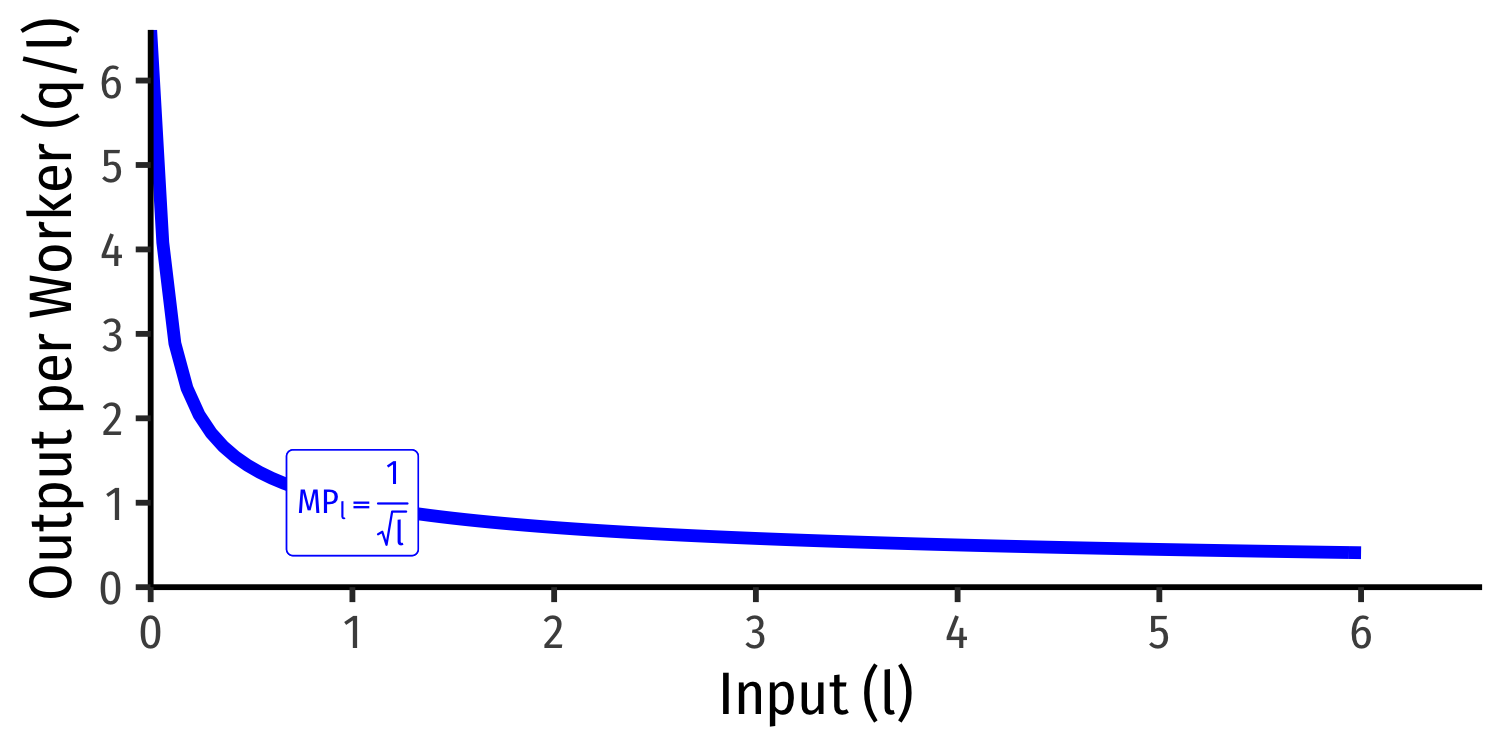
Marginal Product of Labor

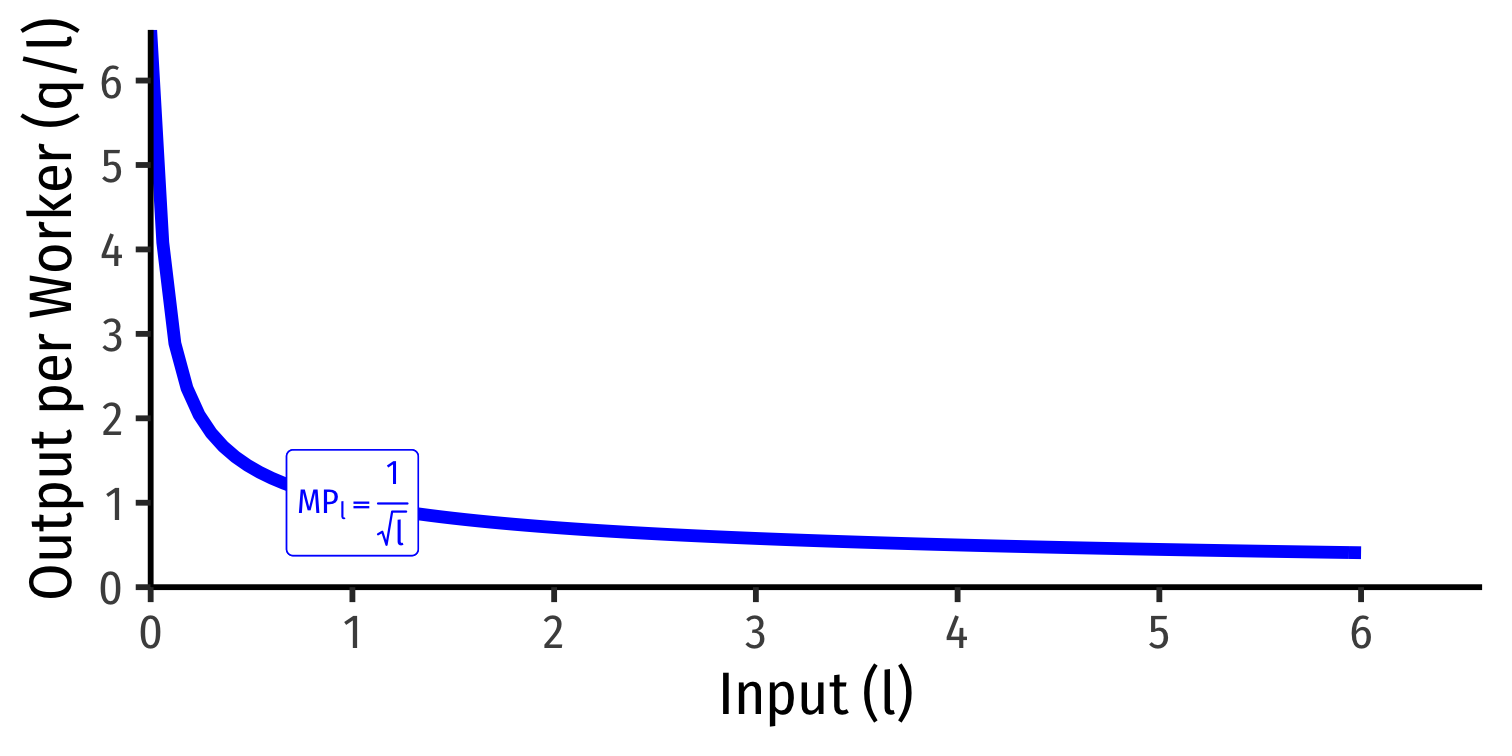
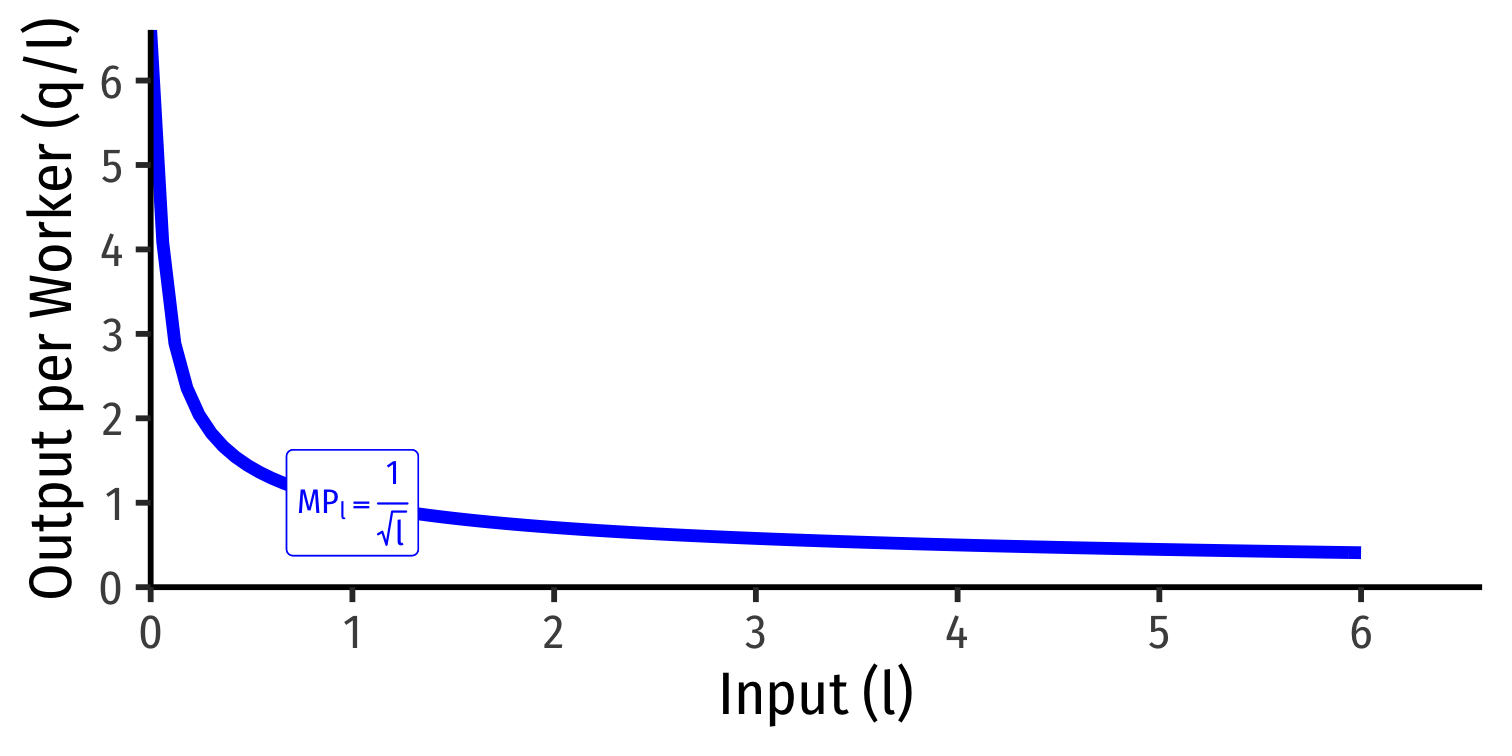
  • Marginal product of labor (MPl): additional output produced by adding one more unit of labor (holding k constant) MPl=ΔqΔl

  • MPl is slope of TP at each value of l!

  • Note: via calculus: ∂q∂l

Marginal Product of Capital

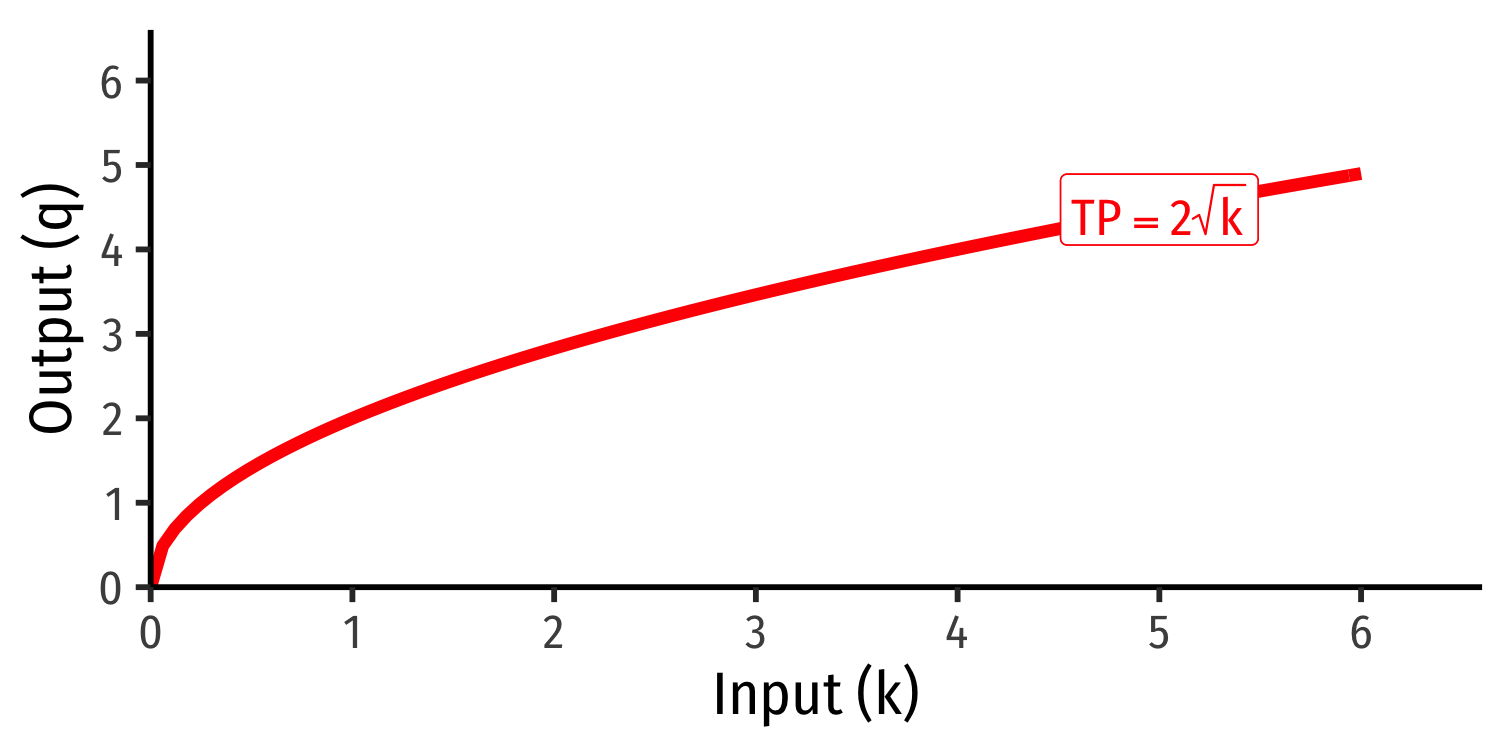
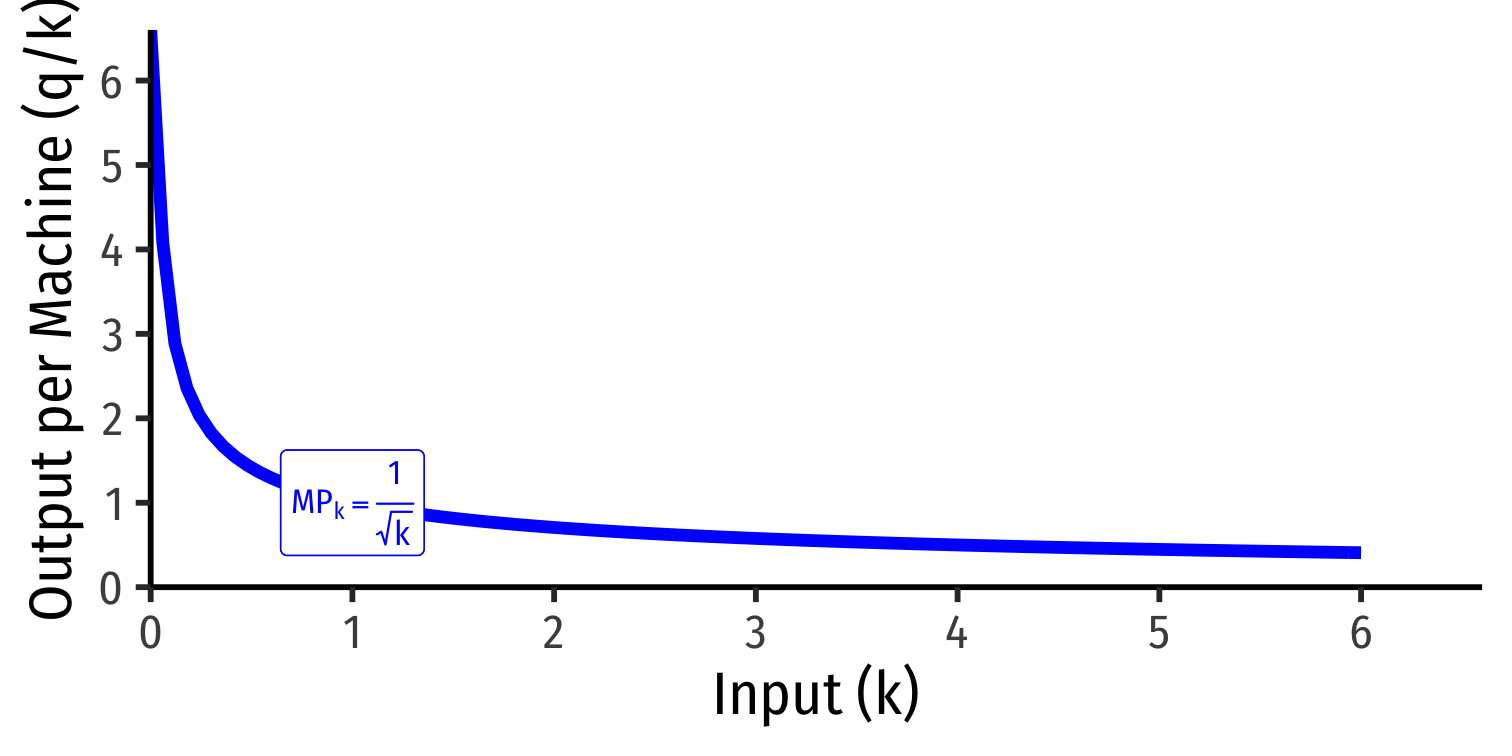
  • Marginal product of capital (MPk): additional output produced by adding one more unit of capital (holding l constant) MPk=ΔqΔk

  • MPk is slope of TP at each value of k!

  • Note: via calculus: ∂q∂k

  • Note we often don't consider capital in the short run!

Diminishing Returns

  • Law of Diminishing Returns: adding more of one factor of production holding all others constant will result in successively lower increases in output

  • In order to increase output, firm will need to increase all factors!

Diminishing Returns

  • Law of Diminishing Returns: adding more of one factor of production holding all others constant will result in successively lower increases in output

  • In order to increase output, firm will need to increase all factors!

Production Functions and Marginal Product

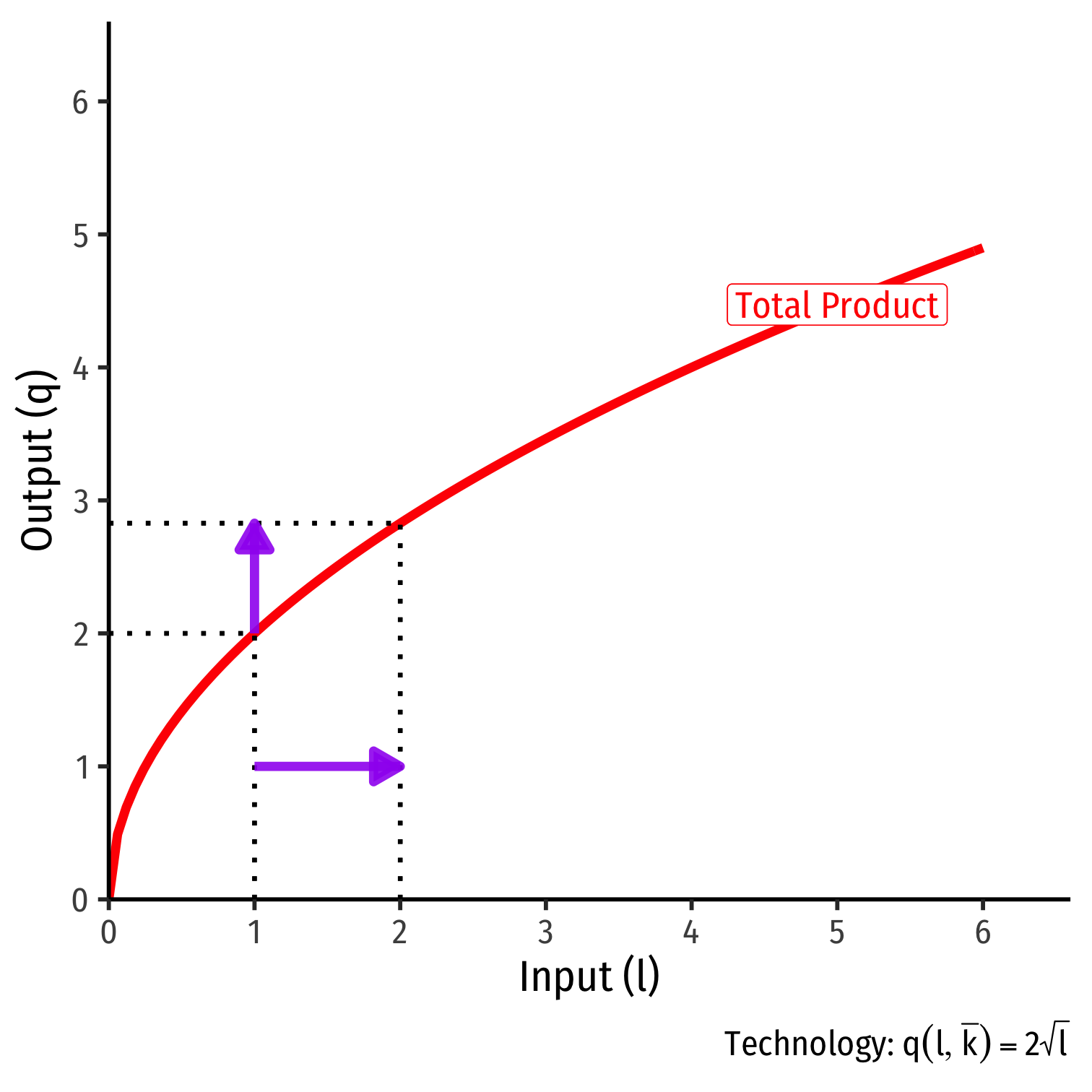
  • A quick trick to roughly estimate MPl

MPl≈q2−q1l2−l1

l q MPl
0 0.00 −
1 2.00 2.00−0.00=2.00
2 2.83 2.83−2.00=0.83
3 3.46 3.46−2.83=0.63
  • Note these are approximate. Technically, MPl is defined via calculus as an infinitesimal change in l, whereas these are discrete changes.

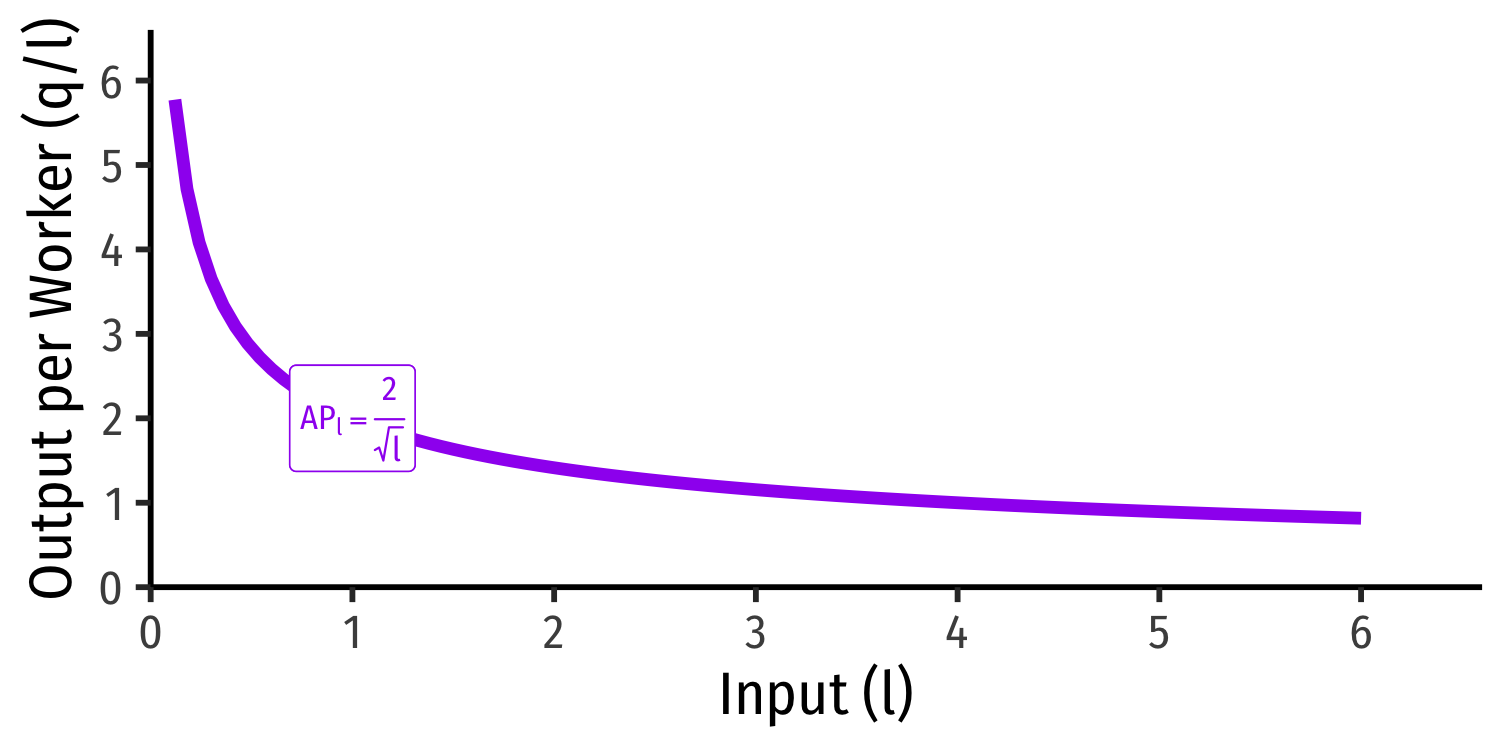
Average Product of Labor (and Capital)

  • Average product of labor (APl): total output per worker APl=ql

  • A measure of labor productivity

  • Average product of capital (APk): total output per unit of capital APk=qk

Production in the Short Run: Example II

Example: Suppose a firm has the following production function: q=2k+l2

  • Suppose in the short run, the firm has 10 units of capital.
  1. Write an equation for the short run production function.
  2. Calculate the total product(s), marginal product(s), and average product(s) for each of the first 5 workers.

The Firm's Problem: Long Run

The Long Run

  • In the long run, all factors of production are variable

q=f(k,l)

  • Can build more factories, open more storefronts, rent more space, invest in machines, etc.

  • So the firm can choose both l and k

The Firm's Problem

  • Based on what we've discussed, we can fill in a constrained optimization model for the firm

    • But don't write this one down just yet!

  • The firm's problem is:

  1. Choose: < inputs and output >

  2. In order to maximize: < profits >

  3. Subject to: < technology >

  • It's actually much easier to break this into 2 stages, though it's possible to do it all at once. See today's class notes page for an example.

The Firm's Two Problems

  • 1st Stage: firm's profit maximization problem:

  1. Choose: < output >

  2. In order to maximize: < profits >

  • We'll cover this later...first we'll explore:

The Firm's Two Problems

  • 1st Stage: firm's profit maximization problem:

  1. Choose: < output >

  2. In order to maximize: < profits >

  • We'll cover this later...first we'll explore:

  • 2nd Stage: firm's cost minimization problem:

  1. Choose: < inputs >

  2. In order to minimize: < cost >

  3. Subject to: < producing the optimal output >

  • Minimizing costs ⟺ maximizing profits

Long Run Production

Example: q=√lk

k
0 1 2 3 4 5
l 0 0.00 0.00 0.00 0.00 0.00 0.00
1 0.00 1.00 1.41 1.73 2.00 2.24
2 0.00 1.41 2.00 2.45 2.83 3.16
3 0.00 1.73 2.45 3.00 3.46 3.87
4 0.00 2.00 2.83 3.46 4.00 4.47
5 0.00 2.24 3.16 3.87 4.47 5.00

  • Many input-combinations yield the same output!

  • So how does the firm choose the optimal combination??

Mapping Input-Combination Choices Graphically

3-D Production Function

2-D Isoquant Contours

Isoquants and MRTS

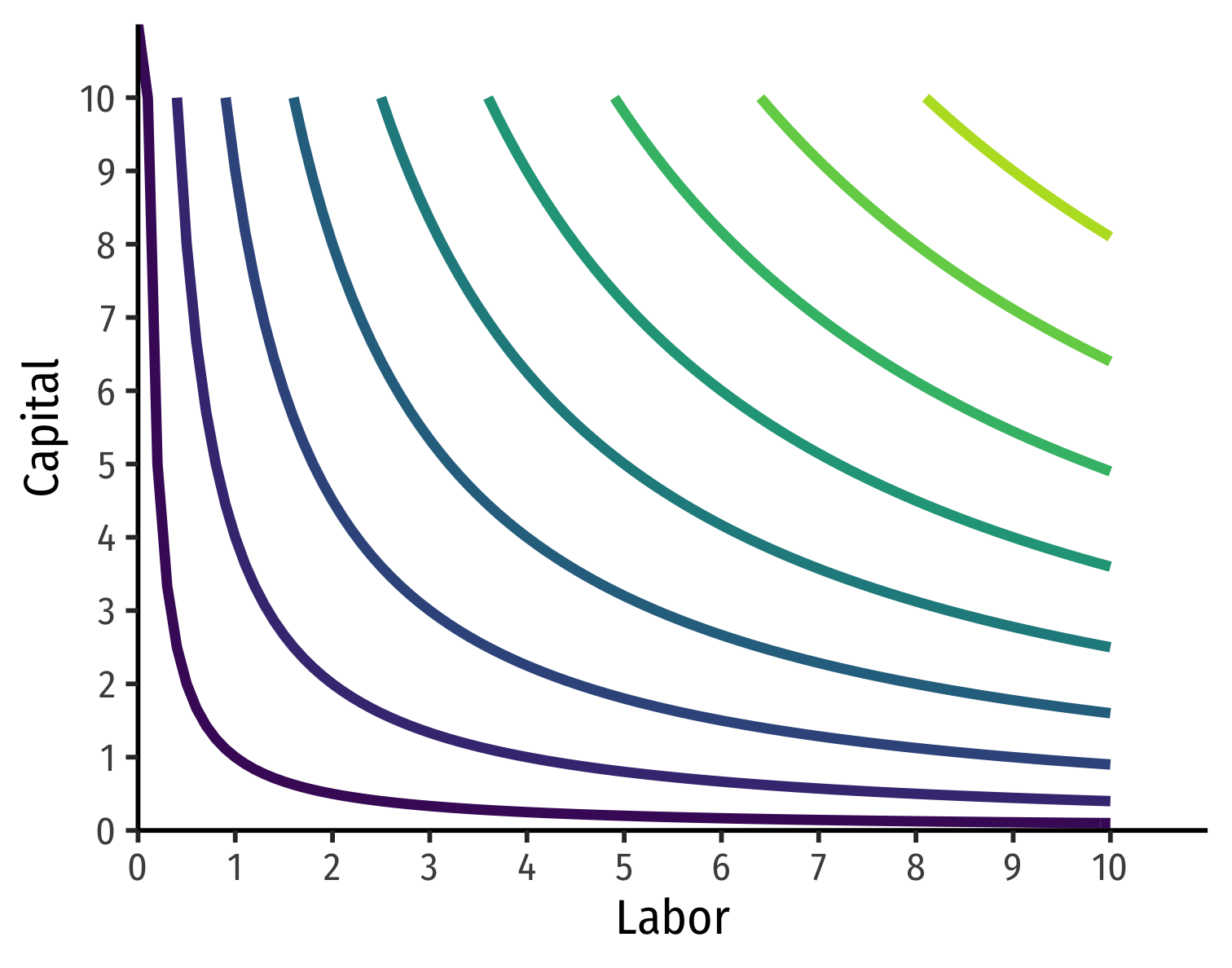
Isoquant Curves

  • We can draw an isoquant indicating all combinations of l and k that yield the same q

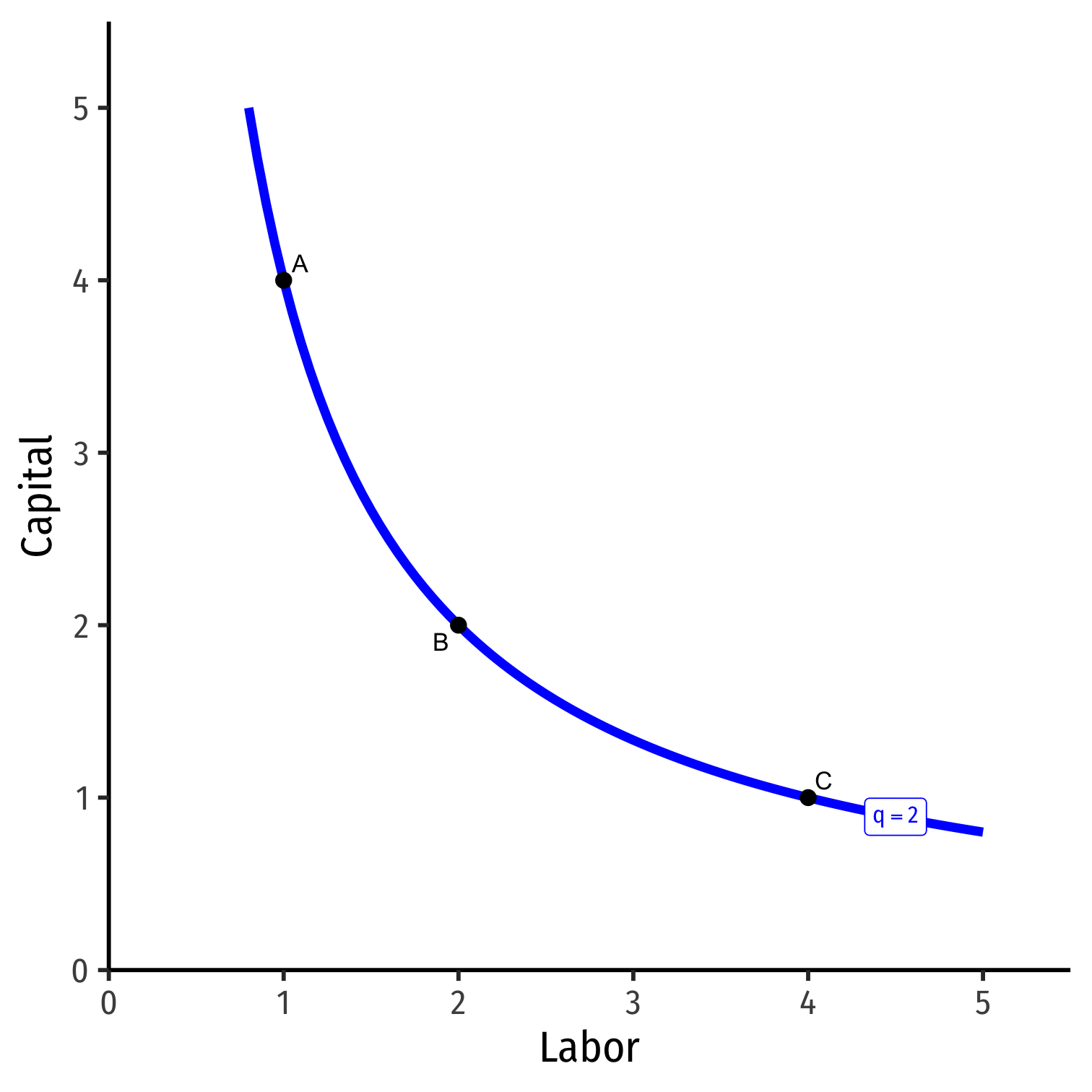
Isoquant Curves

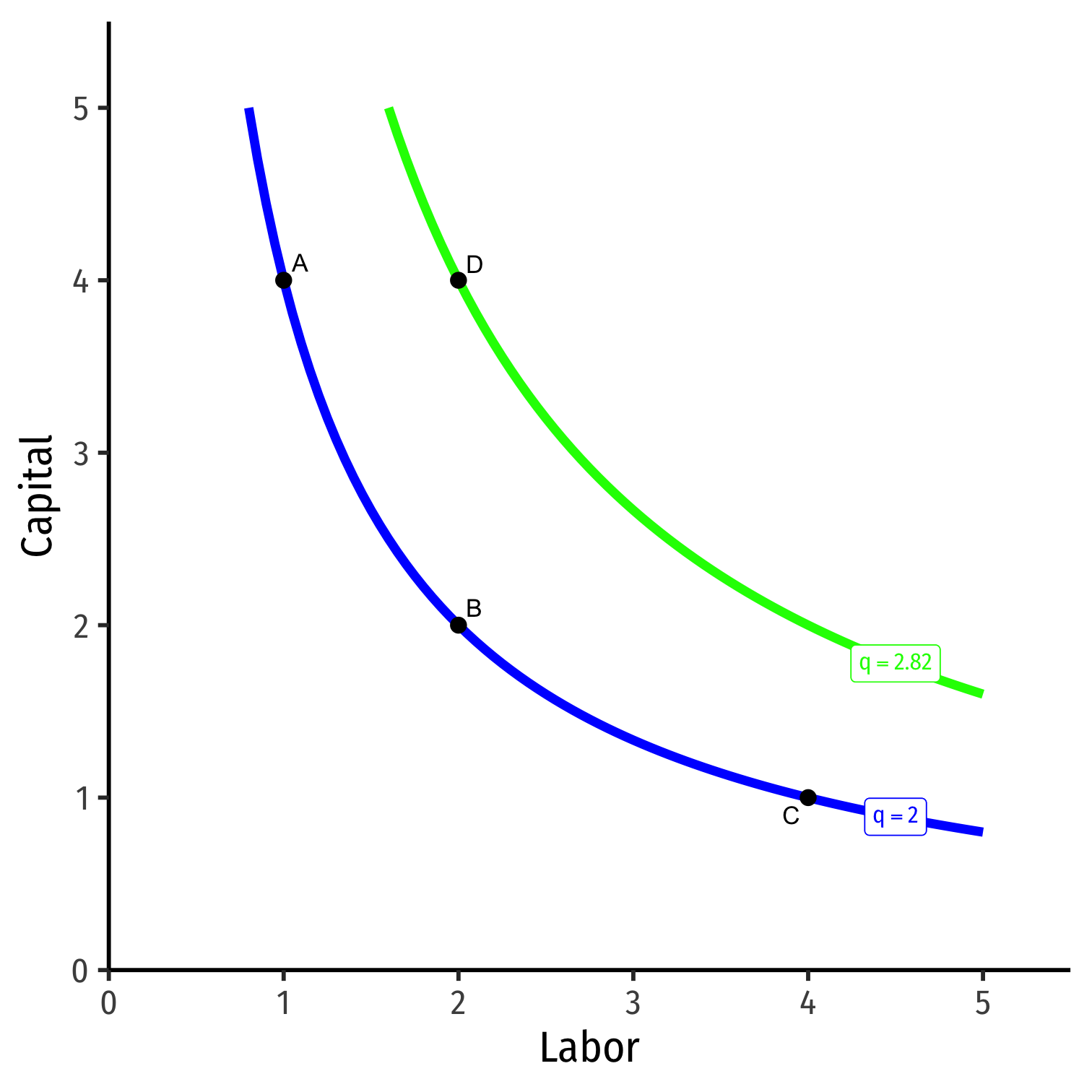
  • We can draw an isoquant indicating all combinations of l and k that yield the same q

  • Combinations above curve yield more output; on a higher curve

    • D>A=B=C

Isoquant Curves

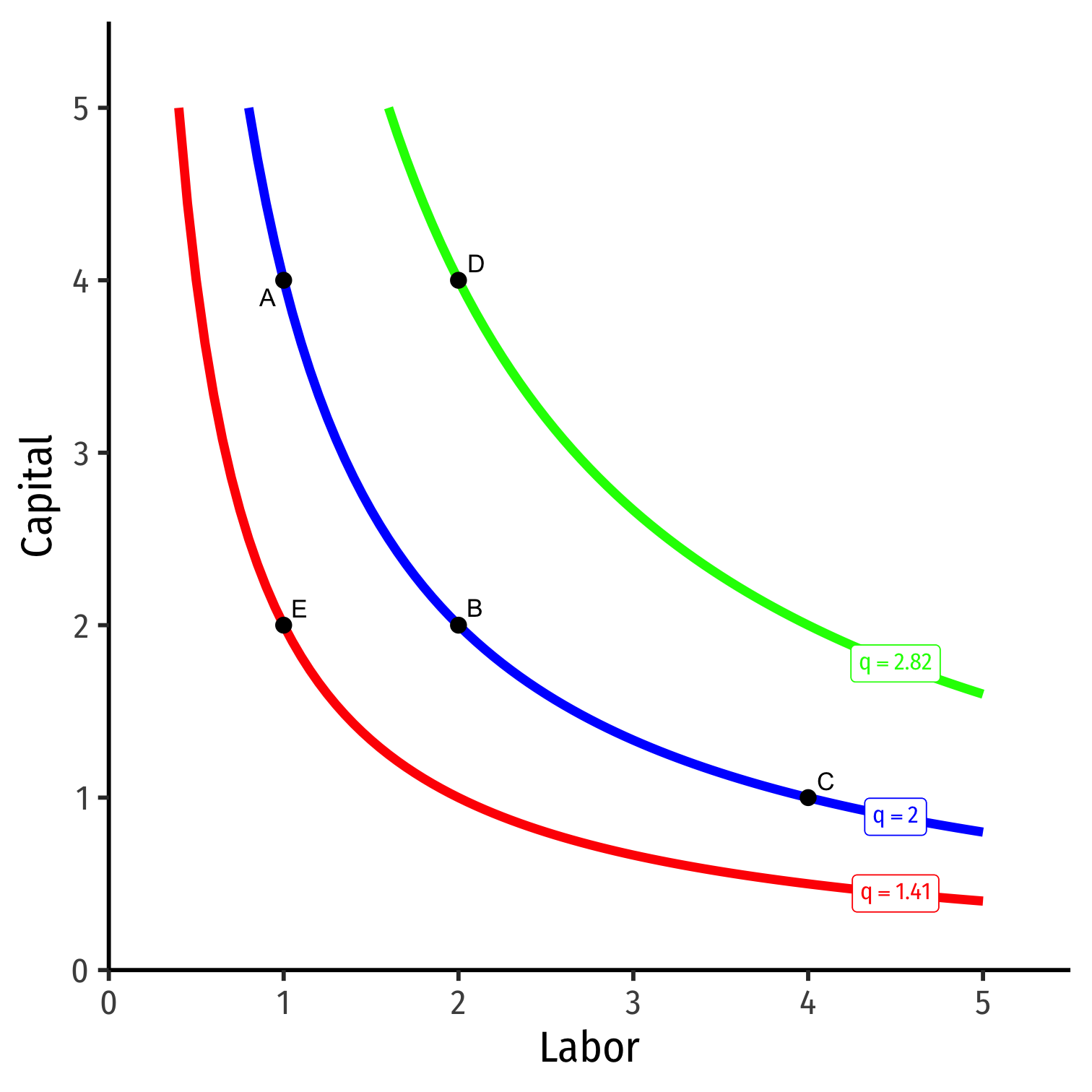
  • We can draw an isoquant indicating all combinations of l and k that yield the same q

  • Combinations above curve yield more output; on a higher curve

    • D>A=B=C

  • Combinations below the curve yield less output; on a lower curve

    • E<A=B=C

Marginal Rate of Technical Substitution I

  • If your firm uses fewer workers, how much more capital would it need to produce the same amount?

Marginal Rate of Technical Substitution I

  • If your firm uses fewer workers, how much more capital would it need to produce the same amount?

  • Marginal Rate of Technical Substitution (MRTS): rate at which firm trades off one input for another to yield the same output

Marginal Rate of Technical Substitution I

  • Think of this as the opportunity cost: # of units of k you need to give up to acquire 1 more l

  • MRTS measures firm's tradeoff between l and k based on its technology

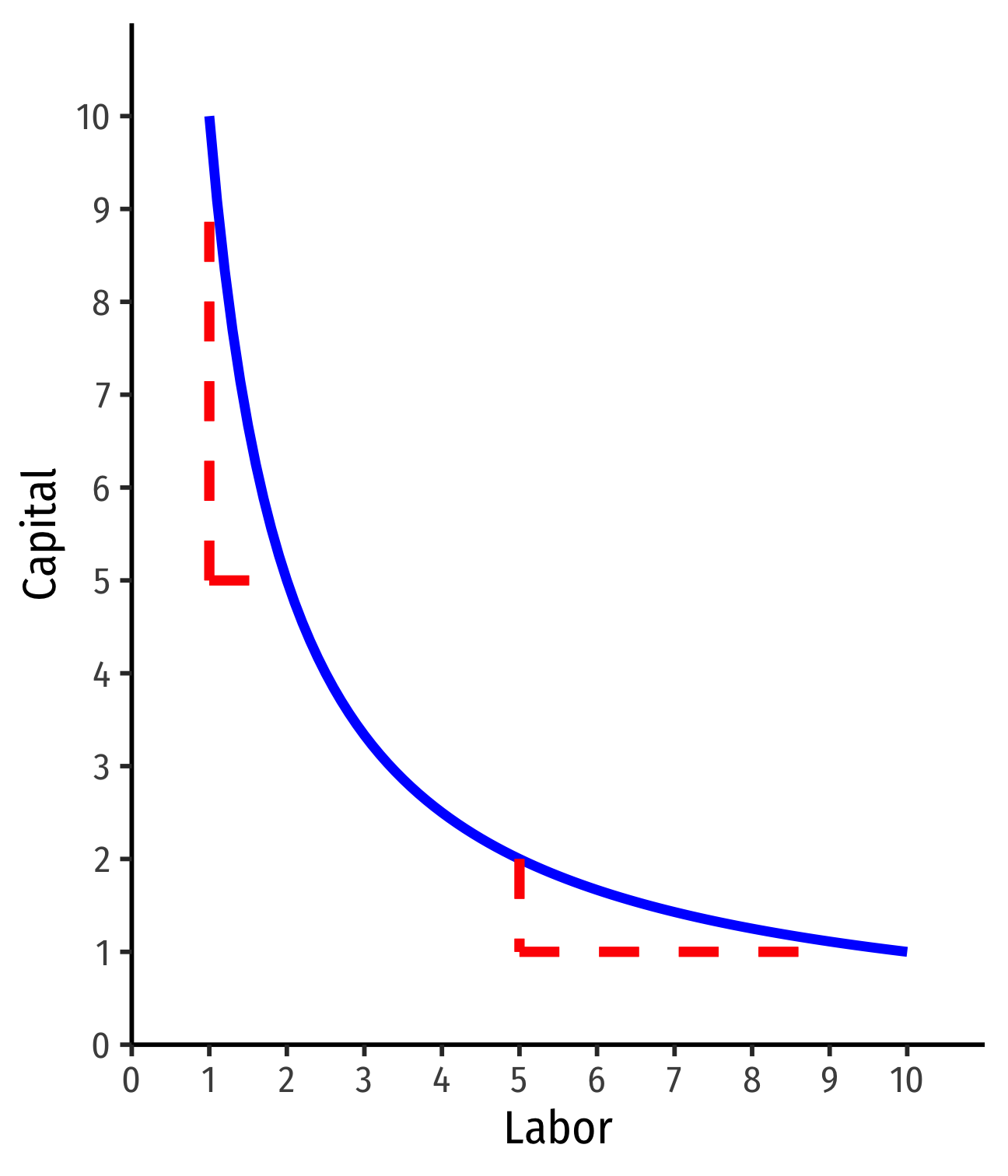
Marginal Rate of Technical Substitution II

  • MRTS is the slope of the isoquant MRTSl,k=−ΔkΔl=riserun

  • Amount of k given up for 1 more l

  • Note: slope (MRTS) changes along the curve!

  • Law of diminishing returns!

MRTS and Marginal Products

  • Relationship between MP and MRTS:

ΔkΔl⏟MRTS=−MPlMPk

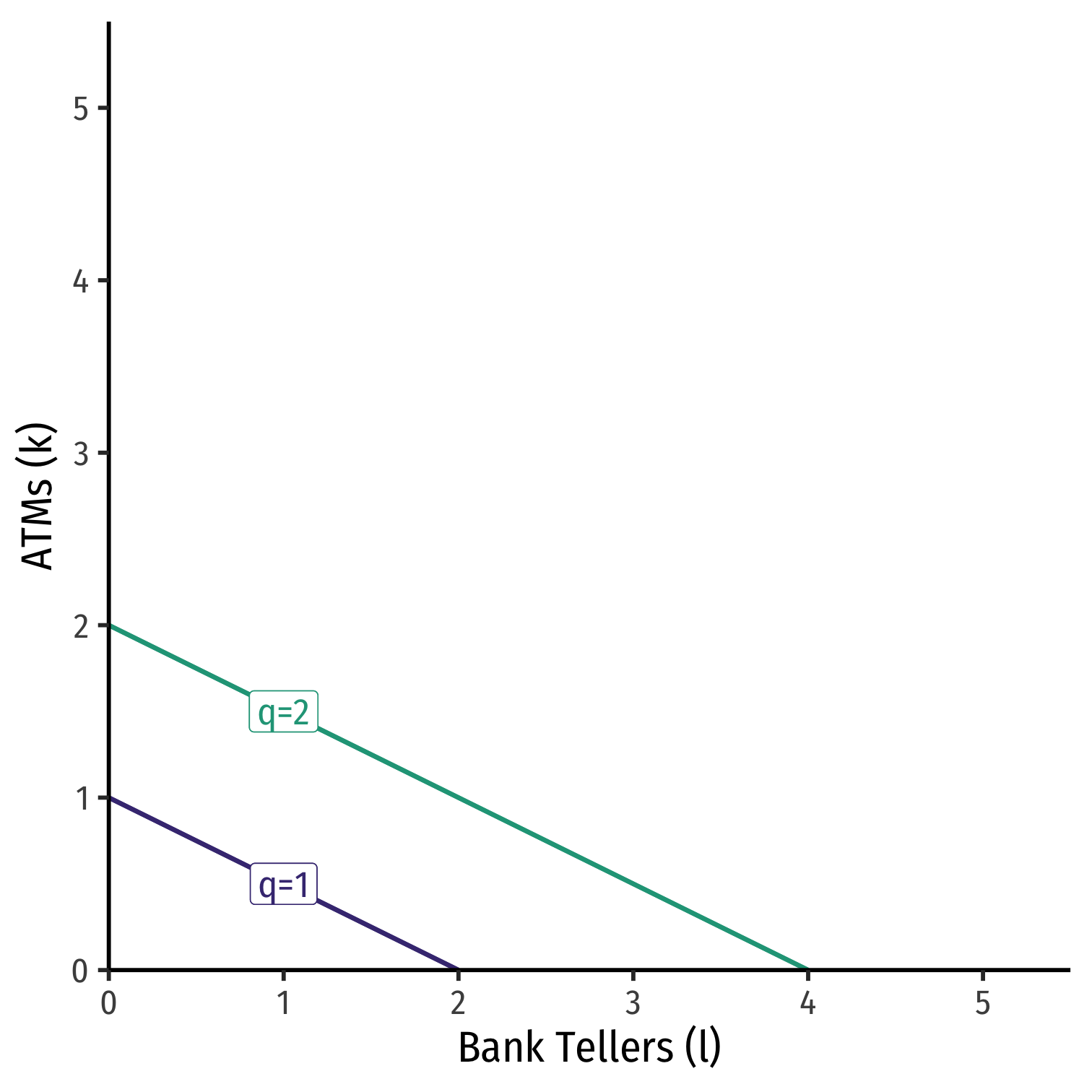
Special Case I: Perfect Substitutes

Example: Consider Bank Tellers (l) and ATMs (k)

  • One ATM can do the work of 2 bank tellers

  • Perfect substitutes: inputs that can be substituted at same fixed rate and yield same output

  • MRTSl,k=−0.5 (a constant!)

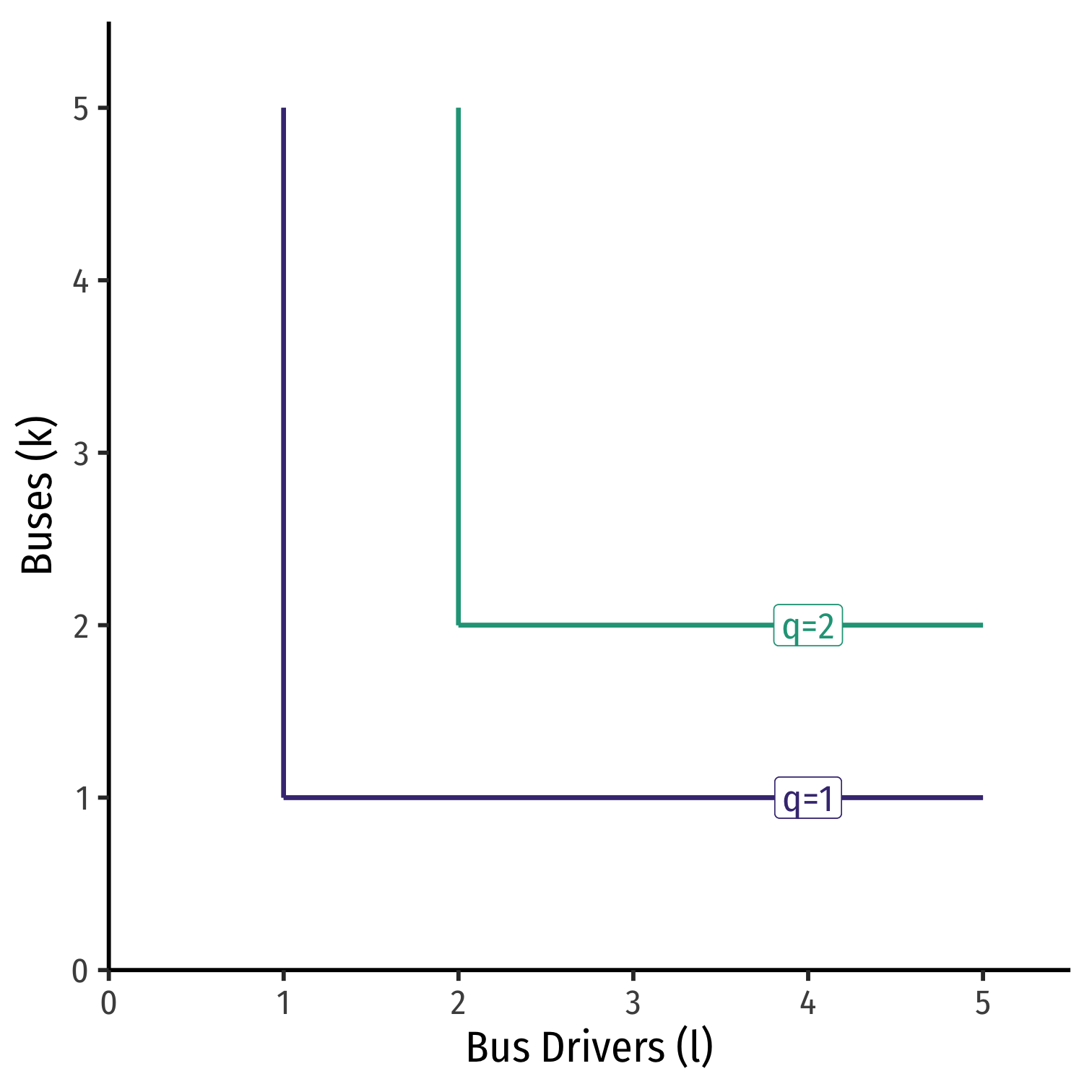
Special Case II: Perfect Complements

Example: Consider busses (k) and bus drivers (l)

  • Must combine together in fixed proportions (1:1)

  • Perfect complements: inputs must be used together in same fixed proportion to produce output

  • MRS: ?

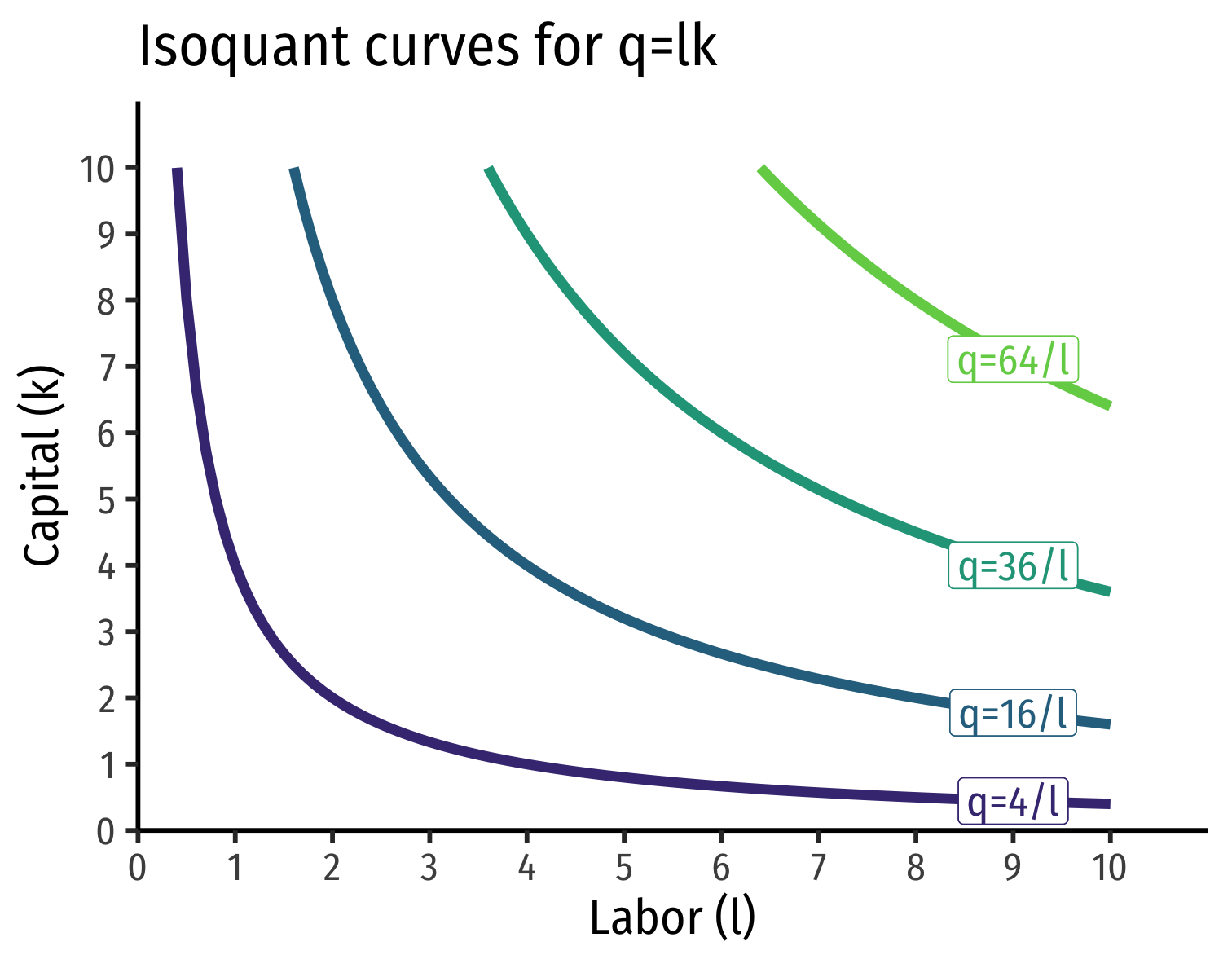
Common Case: Cobb-Douglas Production Functions

  • Again: very common functional form in economics is Cobb-Douglas

q=Akalb

  • Where a,b>0 (and very often a+b=1)

  • A is total factor productivity

Practice

Example: Suppose a firm has the following production function: q=2lk

Where its marginal products are:

MPl=2kMPk=2l

  1. Put l on the horizontal axis and k on the vertical axis. Write an equation for MRTSl,k.

  2. Would input combinations of (1,4) and (2,2) be on the same isoquant?

  3. Sketch a graph of the isoquant from part 2.

Isocost Lines

Isocost Lines

  • If your firm can choose among many input combinations to produce q, which combinations are optimal?

  • Those combination that are cheapest

  • Denote prices of each input as:

    • w: price of labor (wage)
    • r: price of capital

  • Let C be the total cost of using inputs (l,k) at current input prices (w,r) to produce q units of output:

C(w,r,q)=wl+rk

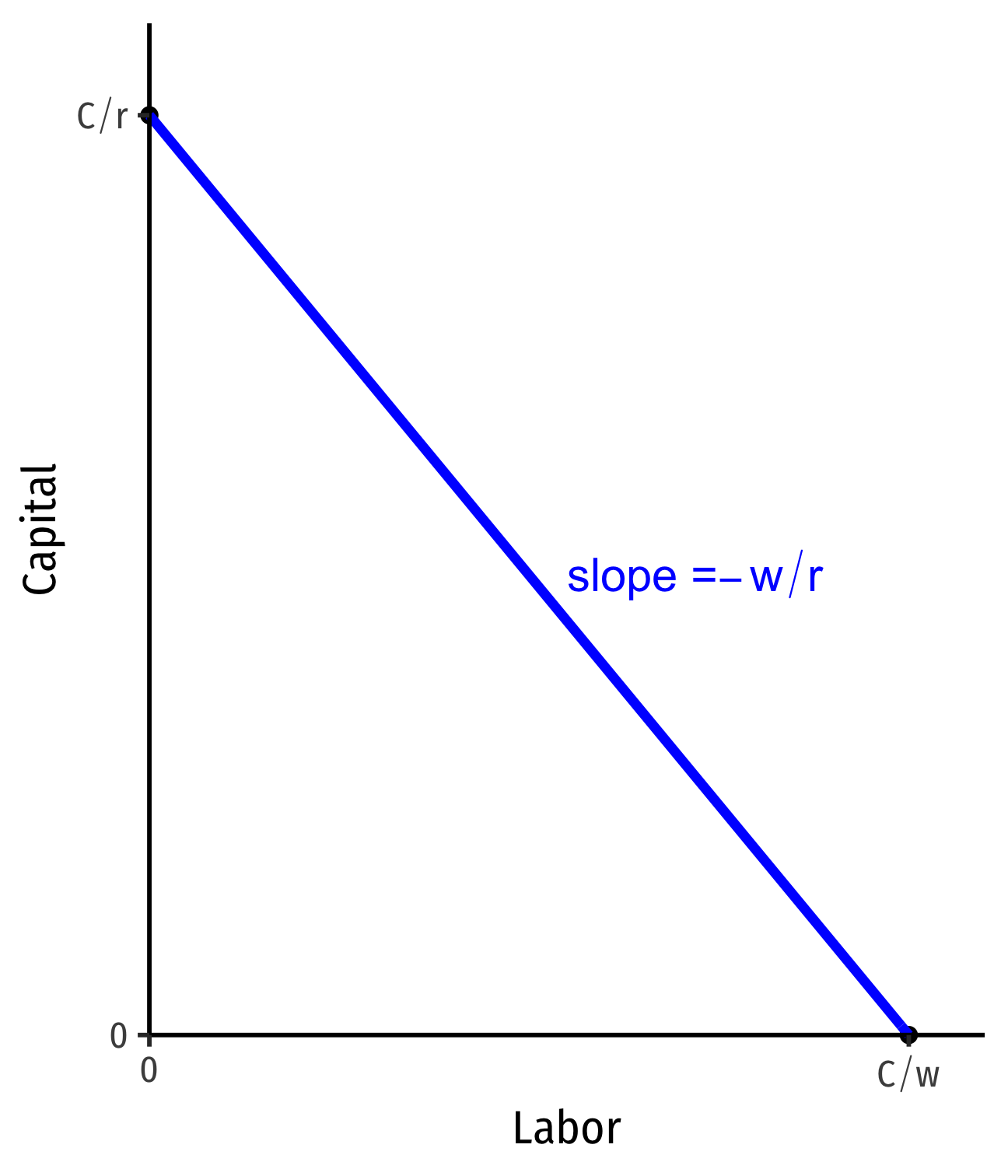
The Isocost Line, Graphically

wl+rk=C

The Isocost Line, Graphically

wl+rk=C

  • Solve for k to graph

k=Cr−wrl

The Isocost Line, Graphically

wl+rk=C

  • Solve for k to graph

k=Cr−wrl

  • Vertical-intercept: Cr
  • Horizontal-intercept: Cw

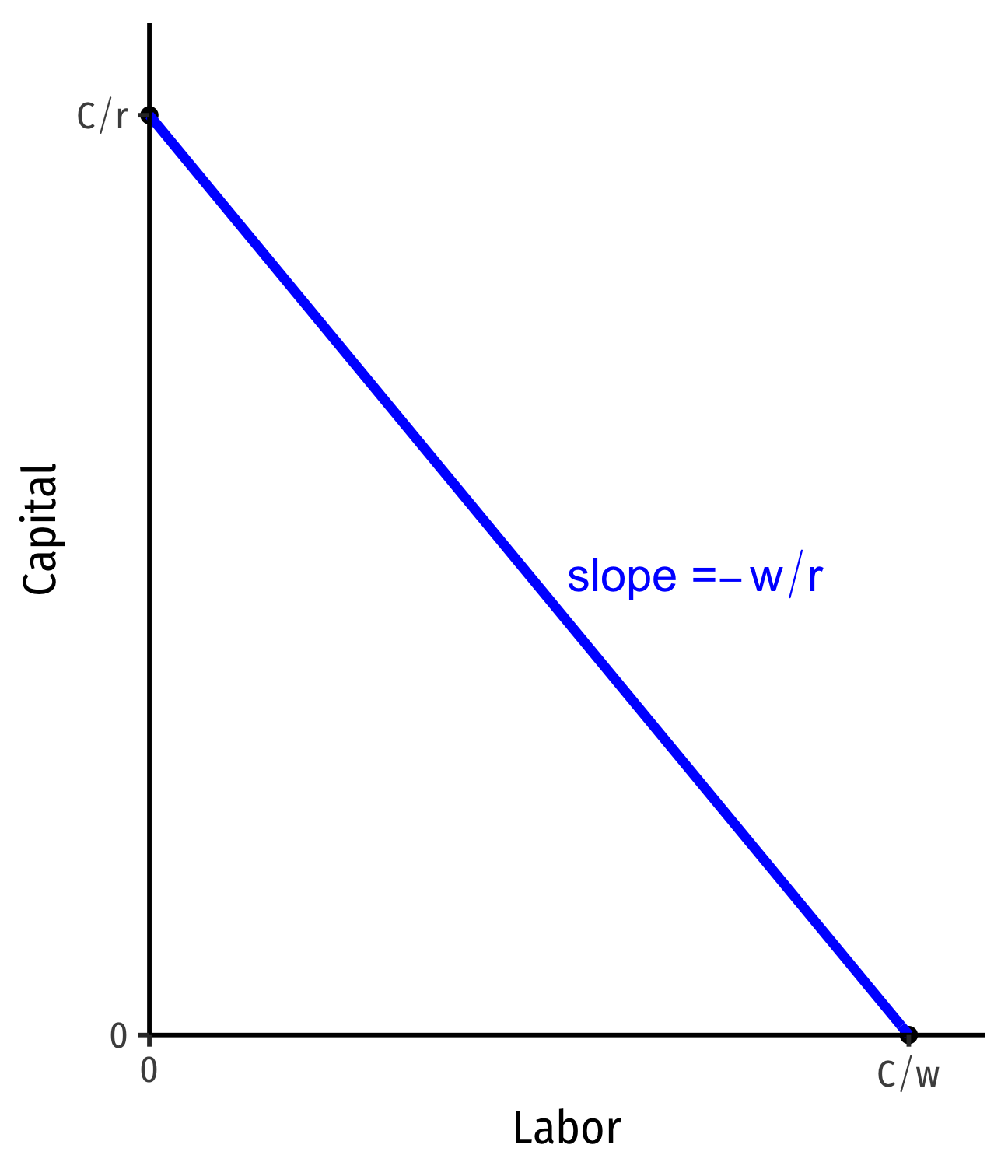
The Isocost Line, Graphically

wl+rk=C

  • Solve for k to graph

k=Cr−wrl

  • Vertical-intercept: Cr
  • Horizontal-intercept: Cw
  • slope: −wr

The Isocost Line: Example

Example: Suppose your firm has a purchasing budget of $50. Market wages are $5/worker-hour and the mark rental rate of capital is $10/machine-hour. Let l be on the horizontal axis and k be on the vertical axis.

  1. Write an equation for the isocost line (in graphable form).

  2. Graph the isocost line.

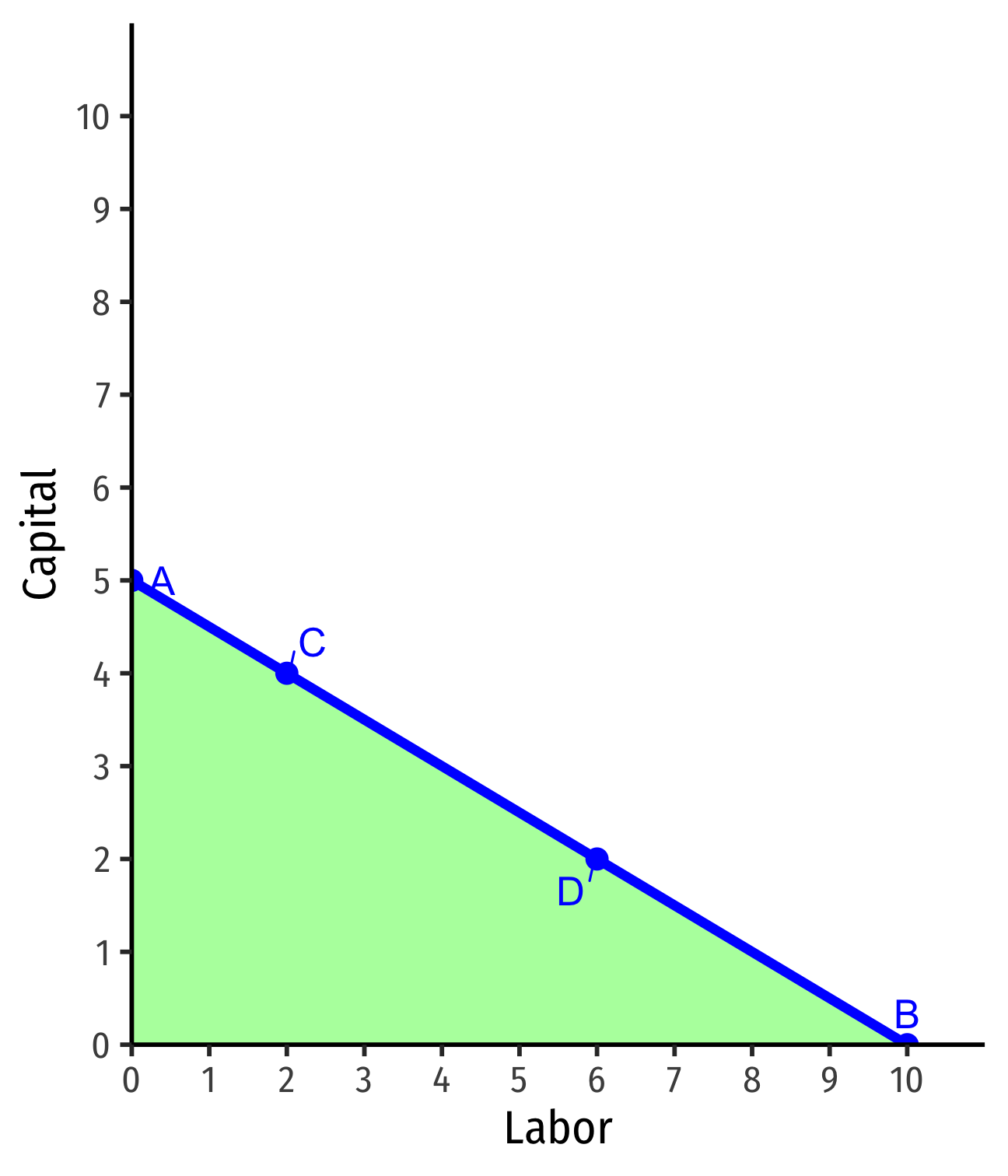
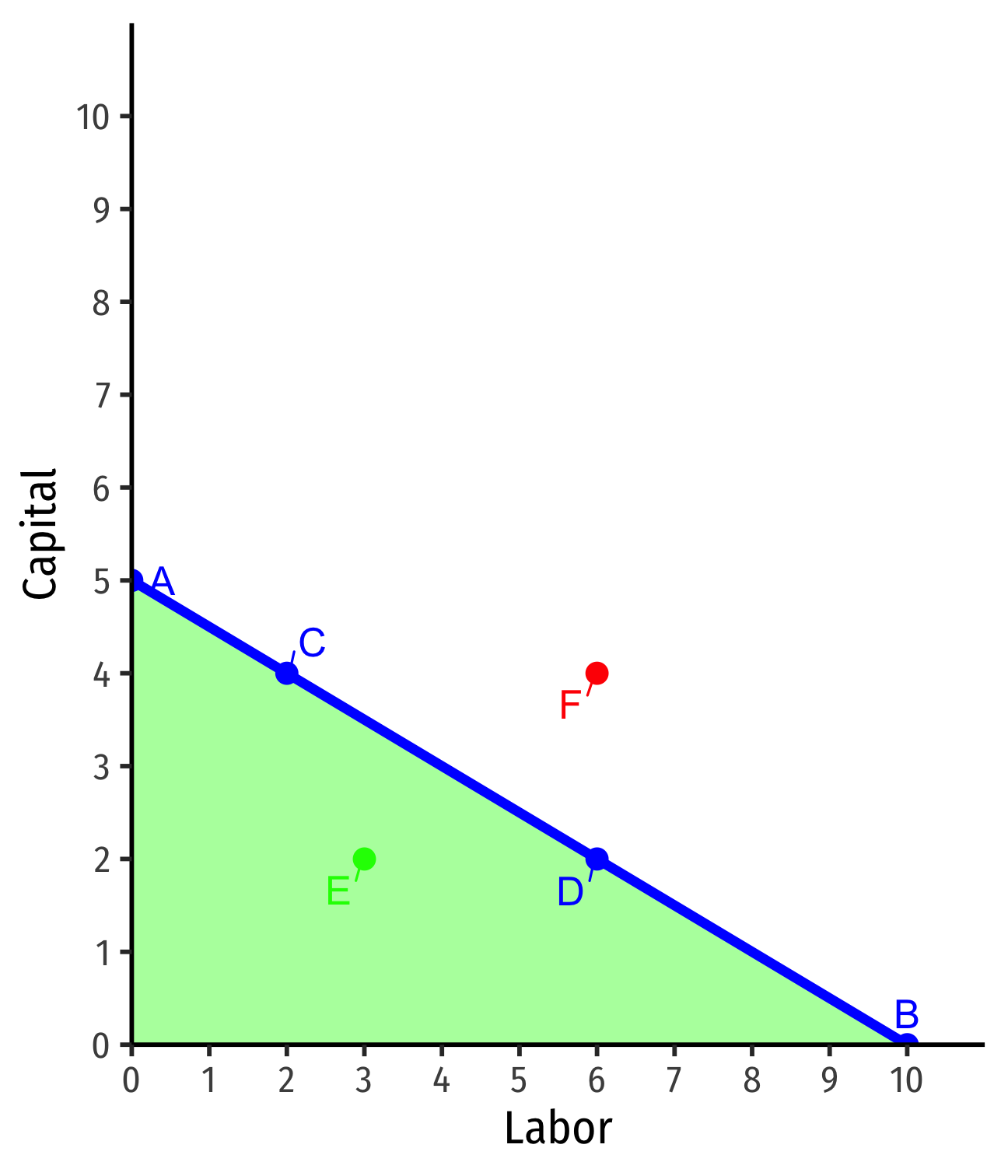
Interpreting Isocost Line

  • Points on the line are same total cost
    • A: $5(0l)+$10(5k)=$50
    • B: $5(10l)+$10(0k)=$50
    • C: $5(2l)+$10(4k)=$50
    • D: $5(6l)+$10(2k)=$50

Interpreting Isocost Line

  • Points on the line are same total cost

    • A: $5(0l)+$10(5k)=$50
    • B: $5(10l)+$10(0k)=$50
    • C: $5(2l)+$10(4k)=$50
    • D: $5(6l)+$10(2k)=$50

  • Points beneath the line are cheaper (but may produce less)

    • E: $5(3l)+$10(2k)=$35

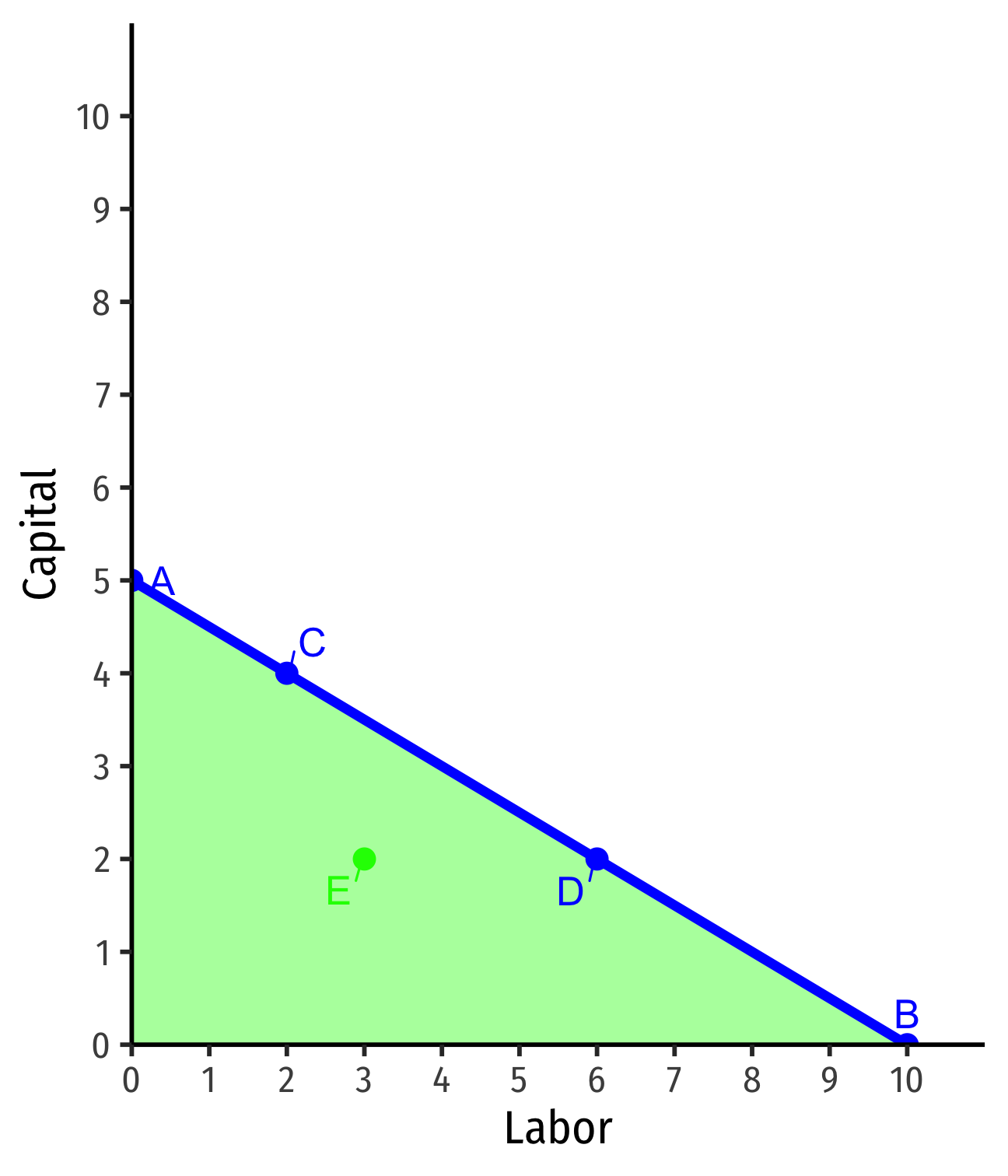
Interpreting the Isocost Line

  • Points on the line are same total cost

    • A: $5(0l)+$10(5k)=$50
    • B: $5(10l)+$10(0k)=$50
    • C: $5(2l)+$10(4k)=$50
    • D: $5(6l)+$10(2k)=$50

  • Points beneath the line are cheaper (but may produce less)

    • E: $5(3l)+$10(2k)=$35

  • Points above the line are more expensive (and may produce more)

    • F: $5(6l)+$10(4k)=$70

Interpretting the Slope

  • Slope: market-rate of tradeoff between l and k

  • Relative price of l or opportunity cost of l:

Using 1 more unit of l requires giving up wr units of k

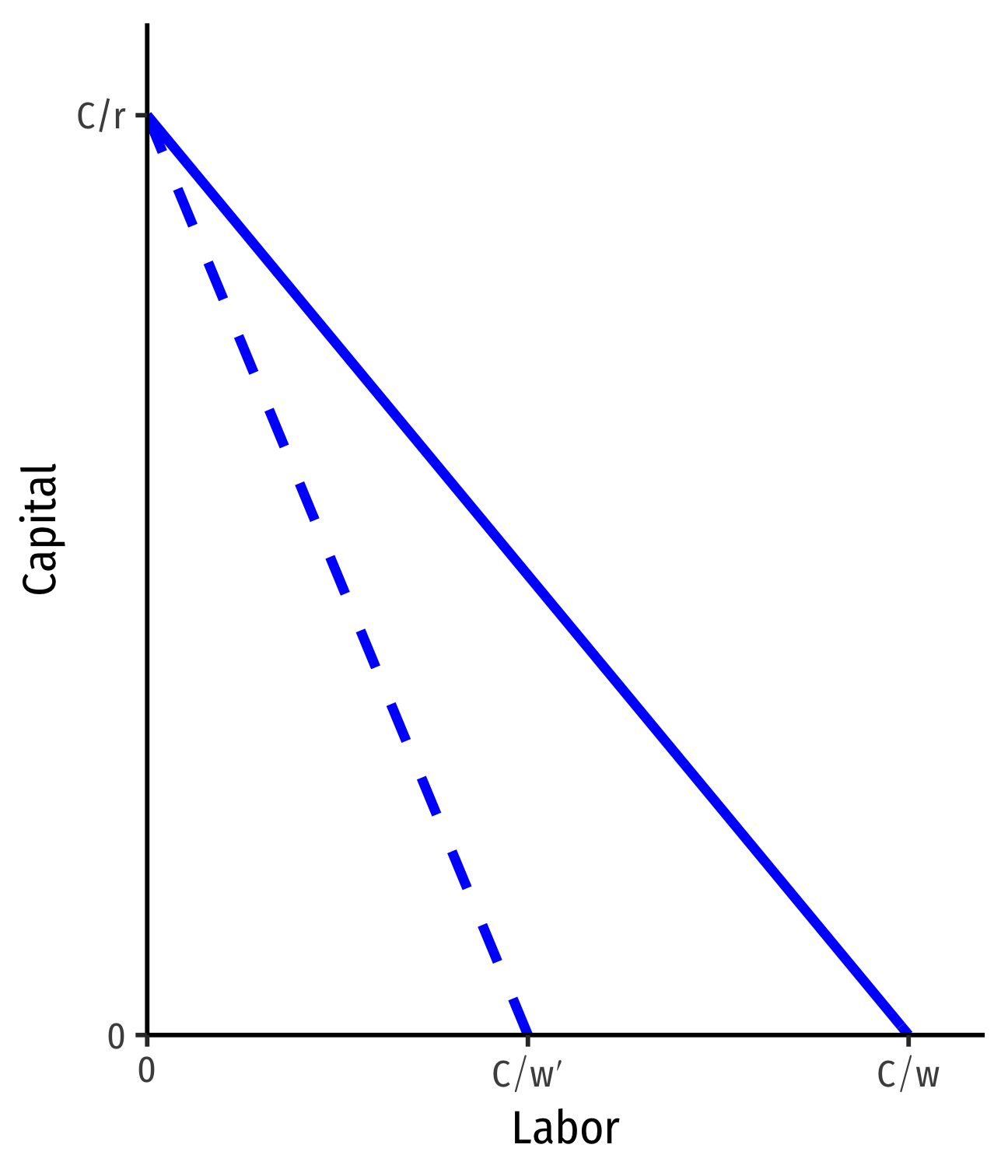
Changes in Relative Factor Prices I

  • Changes in relative factor prices: rotate the line

Example: An increase in the price of l

  • Slope changes: −w′r

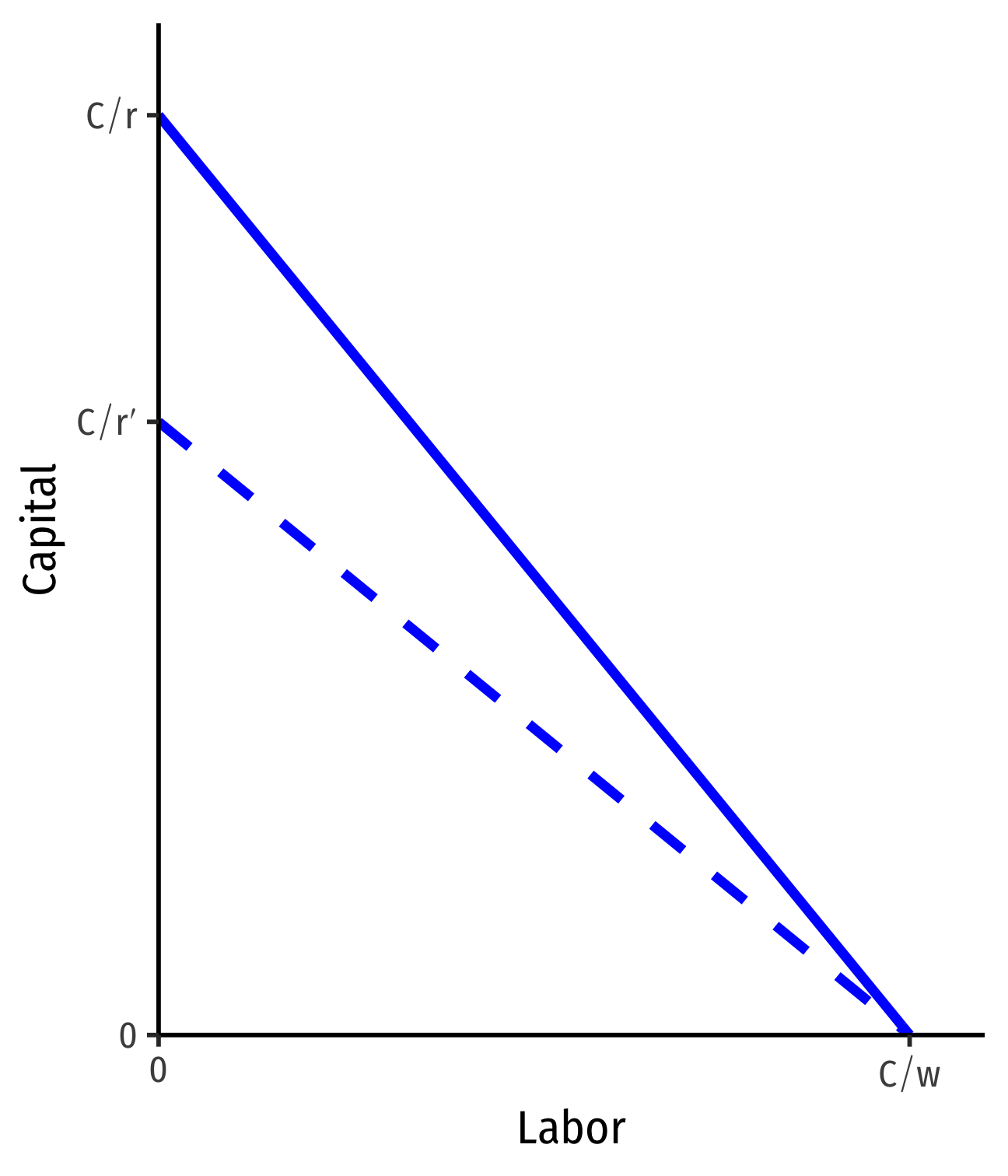
Changes in Relative Factor Prices II

  • Changes in relative factor prices: rotate the line

Example: An increase in the price of k

  • Slope changes: −wr′

The “Runs” of Production

  • “Time”-frame usefully divided between short vs. long run analysis

  • Short run: at least one factor of production is fixed (too costly to change) q=f(ˉk,l)

    • Assume capital is fixed (i.e. number of factories, storefronts, etc)
    • Short-run decisions only about using labor

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow