+ - 0:00:00
Notes for current slide
Notes for next slide

2.4 — Costs of Production

ECON 306 · Microeconomic Analysis · Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microF20
microF20.classes.ryansafner.com

Recall: The Firm's Two Problems

  • 1st Stage: firm's profit maximization problem:

  1. Choose: < output >

  2. In order to maximize: < profits >

  • We'll cover this later...first we'll explore:

  • 2nd Stage: firm's cost minimization problem:

  1. Choose: < inputs >

  2. In order to minimize: < cost >

  3. Subject to: < producing the optimal output >

  • Minimizing costs ⟺ maximizing profits

A Competitive Market

  • We assume (for now) the firm is in a competitive industry:

  1. Firms’ products are perfect substitutes

  2. Firms are “price-takers”, no one firm can affect the market price

  3. Market entry and exit are free†

† Remember this feature. It turns out to be the most important feature that distinguishes different types of industries!

Profit

  • Recall that profit is is: π=pq⏟revenues−(wl+rk)⏟costs

  • We’ll first take a closer look at costs today, then at revenues

  • Next class we'll put them together to find q∗ that maximizes π (the first stage problem)

Opportunity Costs in Production

Costs in Economics are Opportunity Costs

  • Remember, economic costs are different from common conception of "cost"
    • Accounting cost: monetary cost
    • Economic cost: value of next best alternative use of resources given up (i.e. opportunity cost)

Costs in Economics are Opportunity Costs

  • This leads to the difference between

    • Accounting profit: revenues minus accounting costs
    • Economic profit: revenues minues opportunity costs

  • One of the most difficult concepts to think about!

Costs in Economics are Opportunity Costs

  • Another helpful perspective:

  • Accounting cost: what you historically paid for a resource

  • Economic cost: what you can currently get in the market for a selling a resource

    • Resource's value in alternative uses

Costs in Economics are Opportunity Costs

  • Because resources are scarce, and have rivalrous uses,

  • In functioning markets, the market price measures the opportunity cost of using a resource for an alternative use

  • Firms not only pay for direct use of a resource, but also indirectly for "pulling it out" of an alternate use in the economy!

Opportunity Costs in Production

  • Every choice incurs an opportunity cost

Examples:

  • If you choose to start a business, you may give up your salary at your current job
  • If you invest in a factory, you give up other investment opportunities
  • If you use an office building you own, you cannot rent it to other people
  • If you hire a skilled worker, you must pay them a high enough salary to deter them from working for other firms

Opportunity Costs and Economic Profit

Example: Craig's Consulting has the following revenues and costs:

Item Amount
Revenues $600,000
Supplies ($20,000)
Electricity and Water ($10,000)
Employee Salaries ($300,000)
Craig' Salary ($200,000)

Opportunity Costs and Economic Profit

Example: Craig's Consulting has the following revenues and costs:

Item Amount
Revenues $600,000
Supplies ($20,000)
Electricity and Water ($10,000)
Employee Salaries ($300,000)
Craig' Salary ($200,000)
  • Craig could close his firm and rent out the building he owns for $50,000 per year.
  • Instead of running his own business, Craig could work at a larger consulting firm and expect to earn $300,000 per year.

Opportunity Costs and Economic Profit

Example: Craig's Consulting has the following revenues and costs:

Item Amount
Revenues $600,000
Supplies ($20,000)
Electricity and Water ($10,000)
Employee Salaries ($300,000)
Craig' Salary ($200,000)
  • Craig could close his firm and rent out the building he owns for $50,000 per year.
  • Instead of running his own business, Craig could work at a larger consulting firm and expect to earn $300,000 per year.

  1. What is Craig's Consulting's accounting cost? economic cost?

  2. What is Craig's Consulting's accounting profit? economic profit?

Opportunity Cost is Hard for People

Opportunity Costs vs. Sunk Costs

  • Opportunity cost is a forward-looking concept

  • Choices made in the past with non-recoverable costs are called sunk costs

  • Sunk costs should not enter into future decisions

  • Many people have difficulty letting go of unchangeable past decisions: sunk cost fallacy

Sunk Costs: Examples

Sunk Costs: Examples

Sunks Costs: Examples

The Sunk Cost Fallacy

Common Sunk Costs in Business

  • Licensing fees, long-term lease contracts

  • Specific capital (with no alternative use): uniforms, menus, signs

  • Research & Development spending

  • Advertising spending

The Accounting vs. Economic Point of View I

  • Helpful to consider two points of view:

  1. "Accounting point of view": are you taking in more cash than you are spending?

  2. "Economic point of view": is your product you making the best social use of your resources (i.e. are there higher-valued uses of your resources you are keeping them away from)?

The Accounting vs. Economic Point of View II

  • Social implications: are consumers best off with you using scarce resources (with alternative uses!) to produce your current product?

  • Remember: this is an economics course, not a business course!

    • What might be good/bad for one business might have bad/good consequences for society!
    • e.g. monopoly vs. competition

Costs in the Short Run

Costs in the Short Run

  • Total cost function, C(q) relates output q to the total cost of production C

C(q)=f+VC(q)

Costs in the Short Run

  • Total cost function, C(q) relates output q to the total cost of production C

C(q)=f+VC(q)

  • Two kinds of short run costs:

1. Fixed costs, f are costs that do not vary with output

  • Only true in the short run! (Consider this the cost of maintaining your capital)

Costs in the Short Run

  • Total cost function, C(q) relates output q to the total cost of production C

C(q)=f+VC(q)

  • Two kinds of short run costs:

1. Fixed costs, f are costs that do not vary with output

  • Only true in the short run! (Consider this the cost of maintaining your capital)

2. Variable costs, VC(q) are costs that vary with output (notice the variable in them!)

  • Typically, the more production of q, the higher the cost
  • e.g. firm is hiring additional labor

Fixed vs. Variable costs: Examples

Example: Airlines

Fixed costs: the aicraft

Variable costs: getting one more customer in a seat

Fixed vs. Variable costs: Examples

Example: Car Factory

Fixed costs: the factory, machines in the factory

Variable costs: producing one more car

Fixed vs. Variable costs: Examples

Example: Starbucks

Fixed costs: the retail space

Variable costs: producing one more cup of coffee

Fixed vs. Sunk costs

  • Diff. between fixed vs. sunk costs?

  • Sunk costs are a type of fixed cost that are not avoidable or recoverable

  • Many fixed costs can be avoided or changed in the long run

  • Common fixed, but not sunk, costs:

    • rent for office space, durable equipment, operating permits (that are renewed)

  • When deciding to stay in business, fixed costs matter, sunk costs do not!

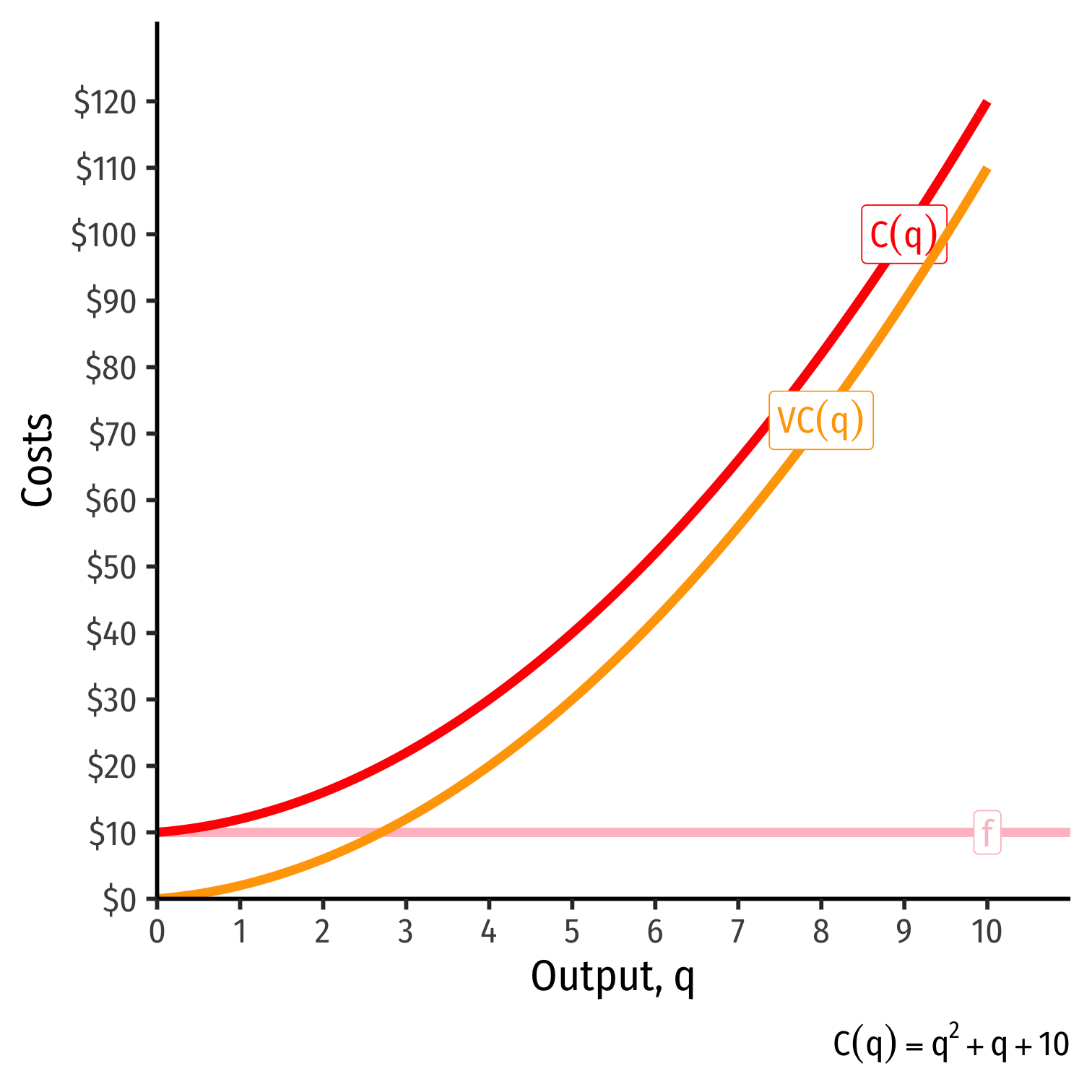
Cost Functions: Example

Example: Suppose your firm has the following total cost function:

C(q)=q2+q+10

  1. Write a function for the fixed costs, f.

  2. Write a function for the variable costs, VC(q).

Cost Functions: Example, Visualized

q f VC(q) C(q)
0 10 0 10
1 10 2 12
2 10 6 16
3 10 12 22
4 10 20 30
5 10 30 40
6 10 42 52
7 10 56 66
8 10 72 82
9 10 90 100
10 10 110 120

Average Costs

  • Average Fixed Cost: fixed cost per unit of output:

AFC(q)=fq

Average Costs

  • Average Fixed Cost: fixed cost per unit of output:

AFC(q)=fq

  • Average Variable Cost: variable cost per unit of output:

AVC(q)=VC(q)q

Average Costs

  • Average Fixed Cost: fixed cost per unit of output:

AFC(q)=fq

  • Average Variable Cost: variable cost per unit of output:

AVC(q)=VC(q)q

  • Average (Total) Cost: (total) cost per unit of output:

AC(q)=C(q)q

Marginal Cost

  • Marginal Cost is the change in cost for each additional unit of output produced:

MC(q)=ΔC(q)Δq≈C2−C1q2−q1

  • Calculus: first derivative of the cost function

  • Marginal cost is the primary cost that matters in making decisions

    • All other costs are driven by marginal costs
    • This is the main cost that firms can "see"

The Importance of Marginal Cost

Dazexiang Rebellion against the Qin Dynasty (209 B.C.)

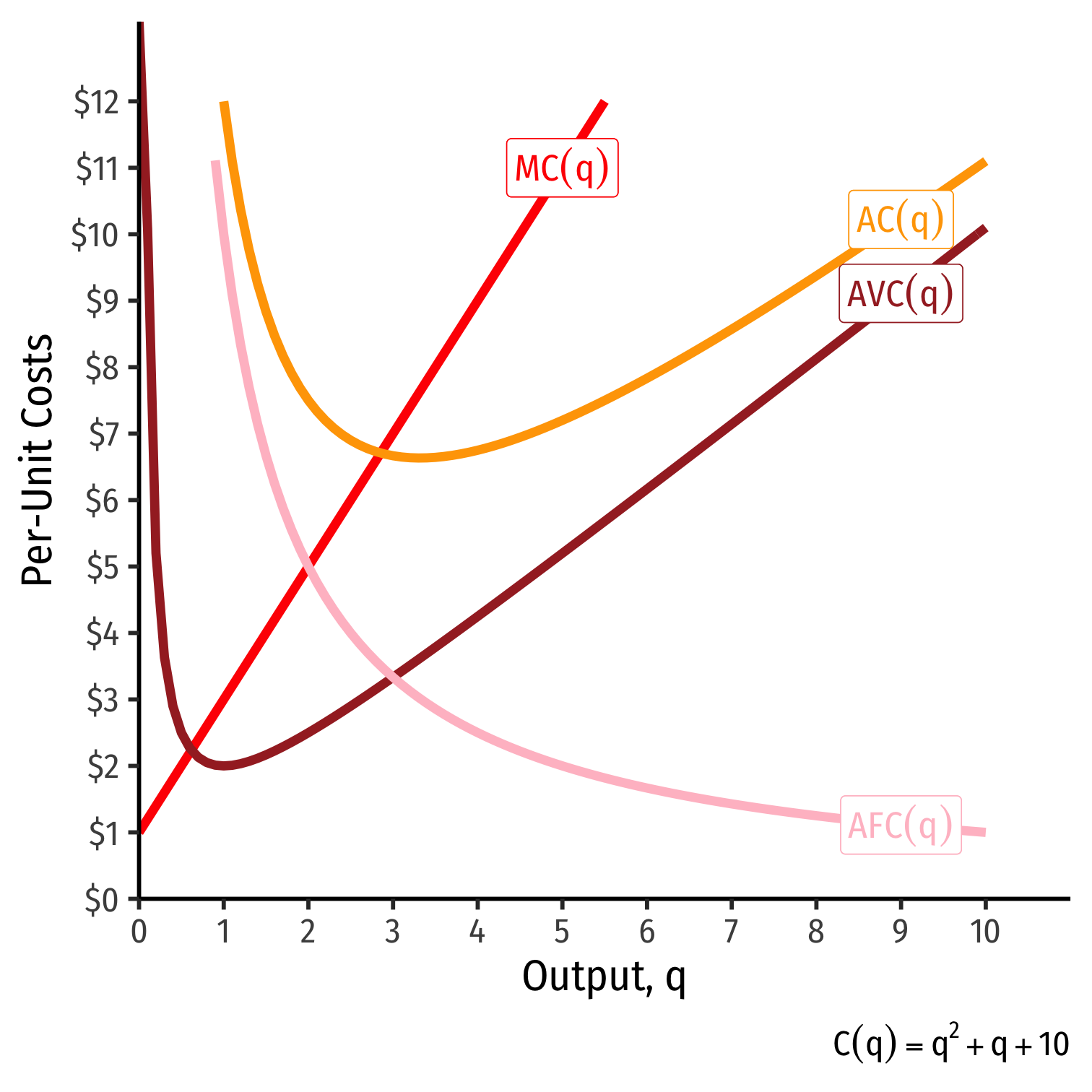
Average and Marginal Costs: Example

Example: A small farm grows strawberries on 5 acres of land that it rents for $200 a week. The farm can hire workers at a wage of $250/week for each worker. The table below shows how the output of strawberries (in truckloads) varies with the number of workers hired:

Output Labor
0 0
1 1
2 3
3 7
4 12
5 18
  1. If labor is the only variable cost, calculate the MC(q) and AC(q) for each of the first 5 truckloads.

Average and Marginal Costs: Visualized

q C(q) MC(q) AFC(q) AVC(q) AC(q)
0 10 − − − −
1 12 2 10.00 2 12.00
2 16 4 5.00 3 8.00
3 22 6 3.33 4 7.30
4 30 8 2.50 5 7.50
5 40 10 2.00 6 8.00
6 52 12 1.67 7 8.70
7 66 14 1.43 8 9.40
8 82 16 1.25 9 10.25
9 100 18 1.11 10 11.10
10 120 20 1.00 11 12.00

Relationship Between Marginal and Average

  • Relationship between a marginal and an average value:

  • marginal > average, average ↑

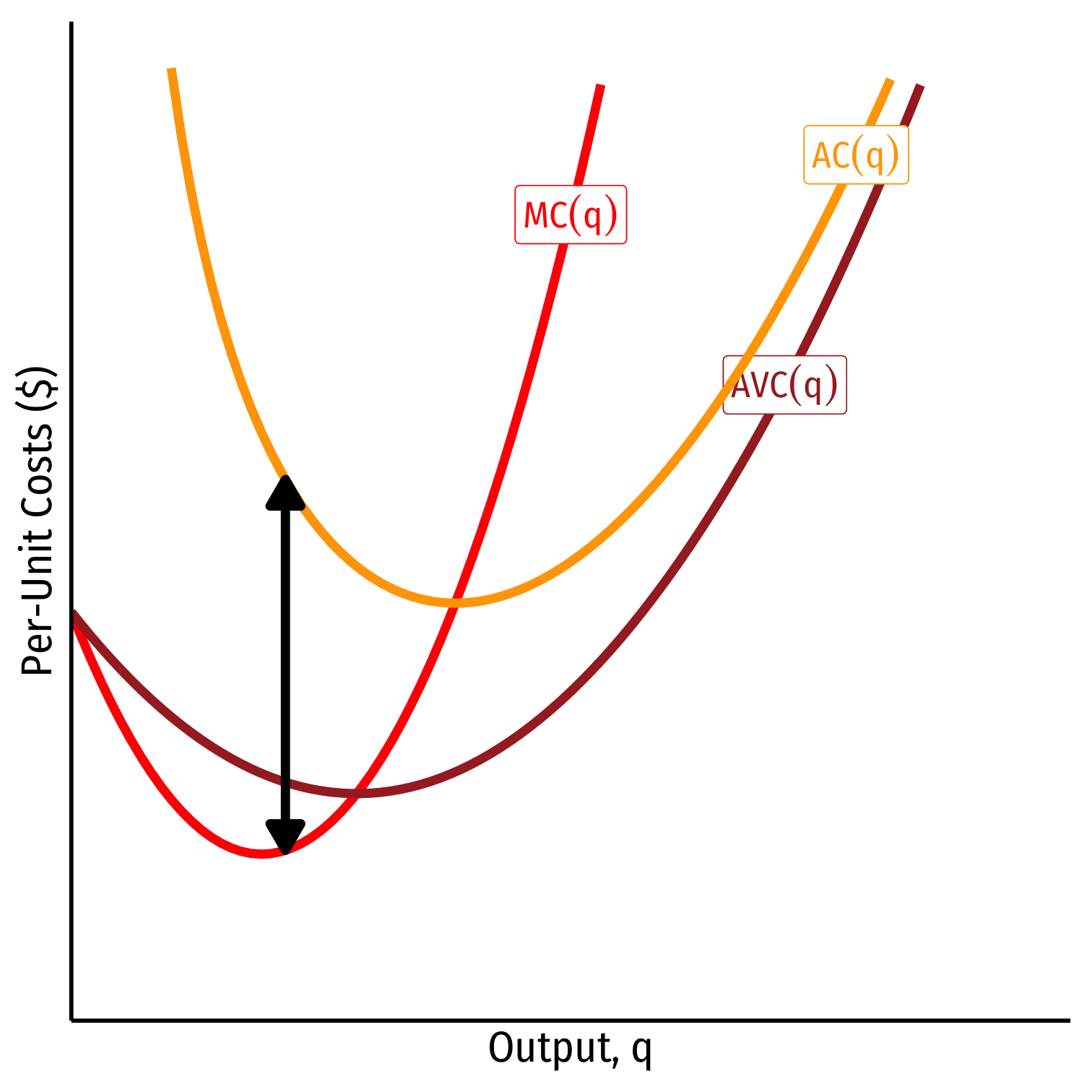
Relationship Between Marginal and Average

  • Relationship between a marginal and an average value:

  • marginal > average, average ↑

  • marginal < average, average ↓

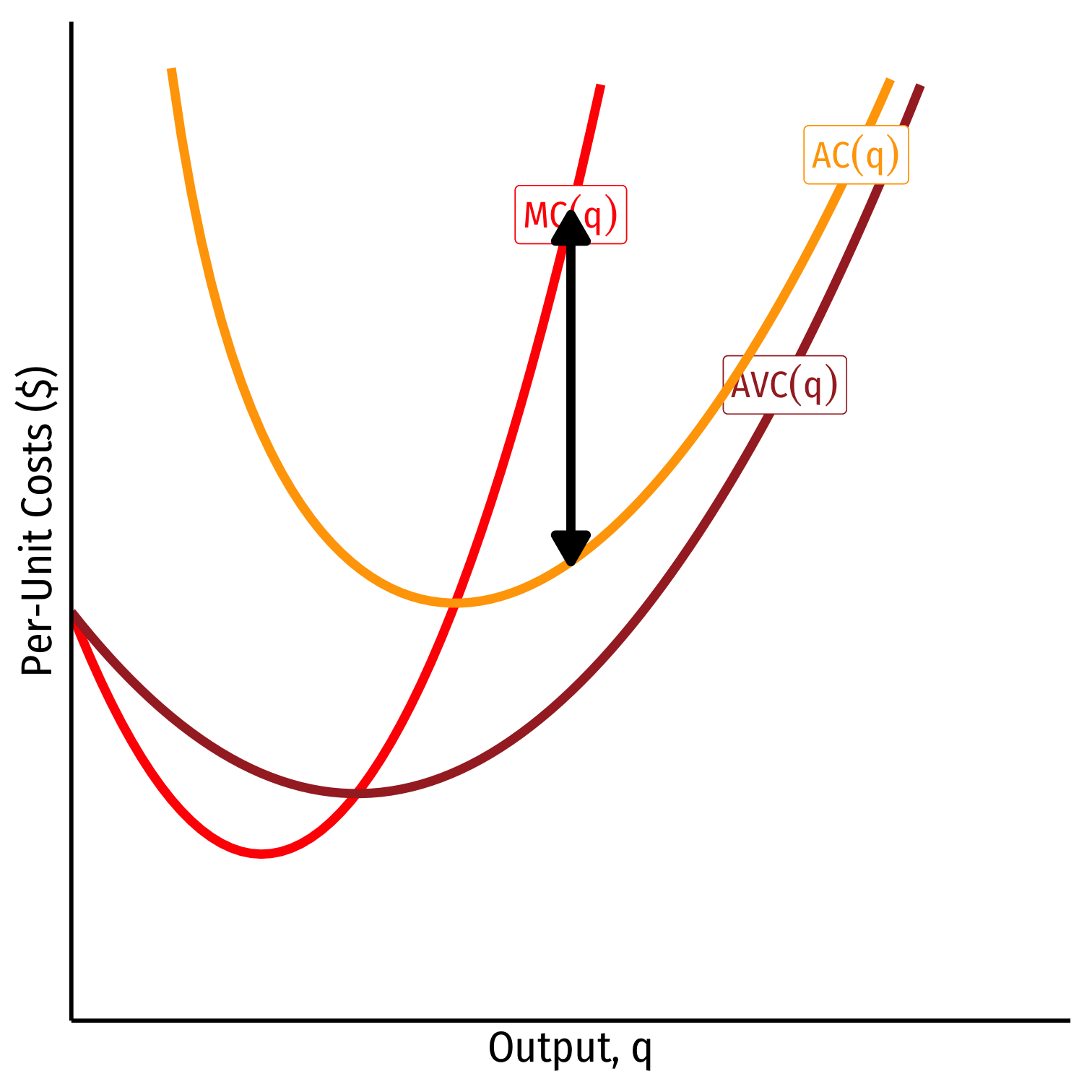
Relationship Between Marginal and Average

  • Relationship between a marginal and an average value:

  • marginal > average, average ↑

  • marginal < average, average ↓

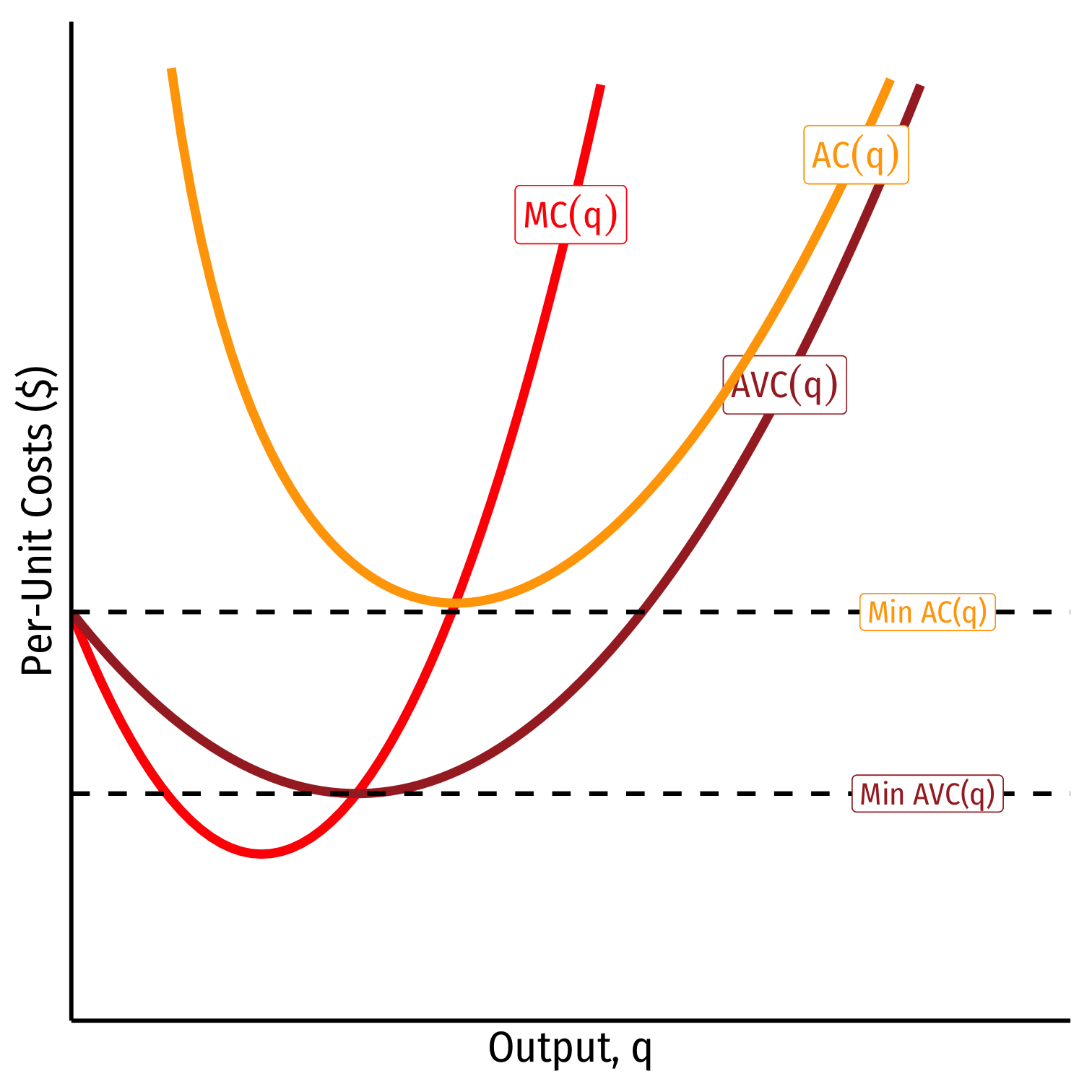
  • When marginal = average, average is maximized/minimized

  • When MC=AC, AC is at a minimum

  • When MC=AVC, AVC is at a minimum

  • Economic importance (later): Break-even price and shut-down price

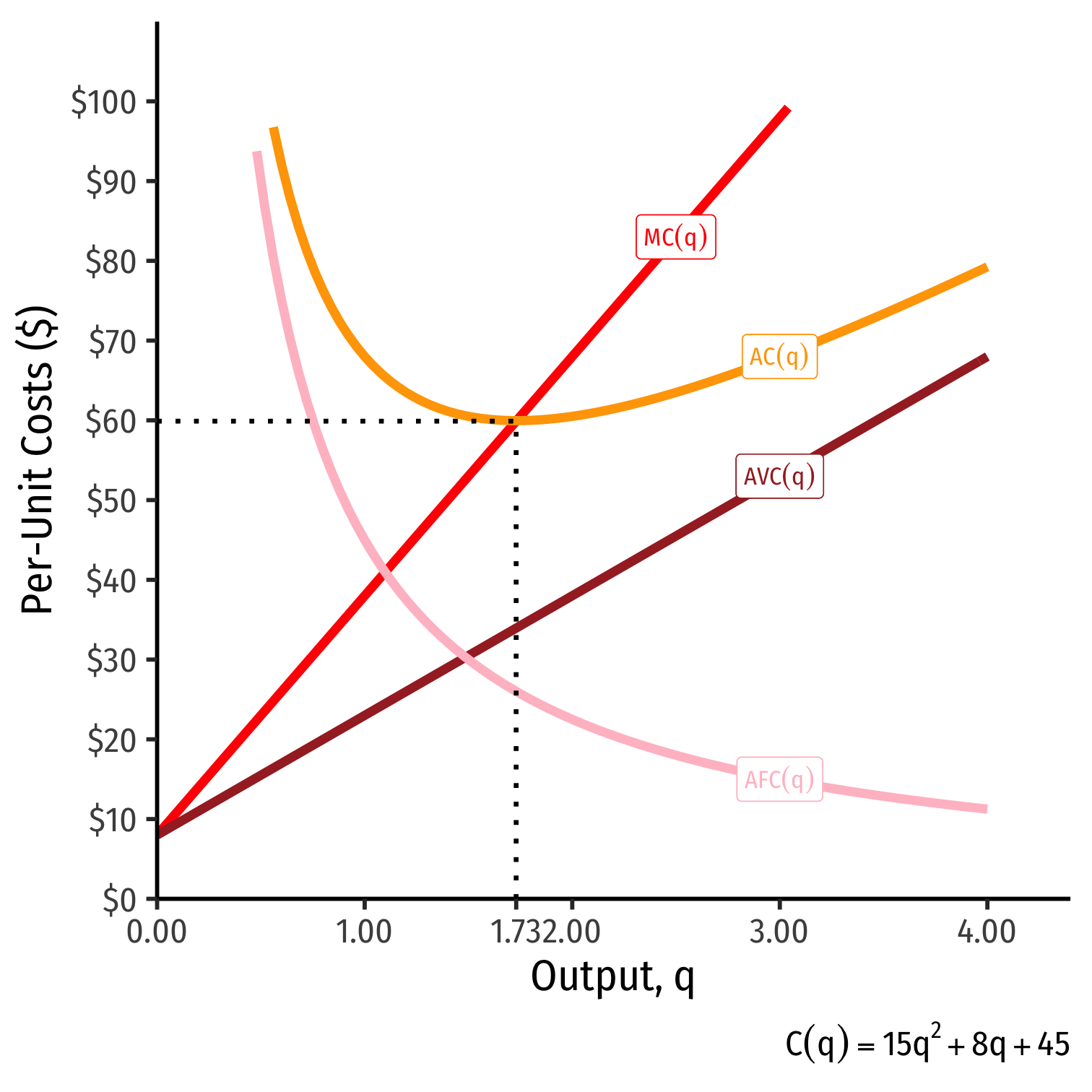
Short Run Costs: Example

Example: Suppose a firm's cost structure is described by: C(q)=15q2+8q+45MC(q)=30q+8

  1. Write expressions for the firm's fixed costs, variable costs, average fixed costs, average variable costs, and average (total) costs.

  2. Find the minimum average (total) cost.

  3. Find the minimum average variable cost.

Costs: Example: Visualized

Costs in the Long Run

Costs in the Long Run

  • Long run: firm can change all factors of production & vary scale of production

  • Long run average cost, LRAC(q): cost per unit of output when the firm can change both l and k to make more q

  • Long run marginal cost, LRMC(q): change in long run total cost as the firm produce an additional unit of q (by changing both l and/or k)

Average Cost in the Long Run

  • Long run: firm can choose k (factories, locations, etc)

  • Separate short run average cost (SRAC) curves for each amount of k potentially chosen

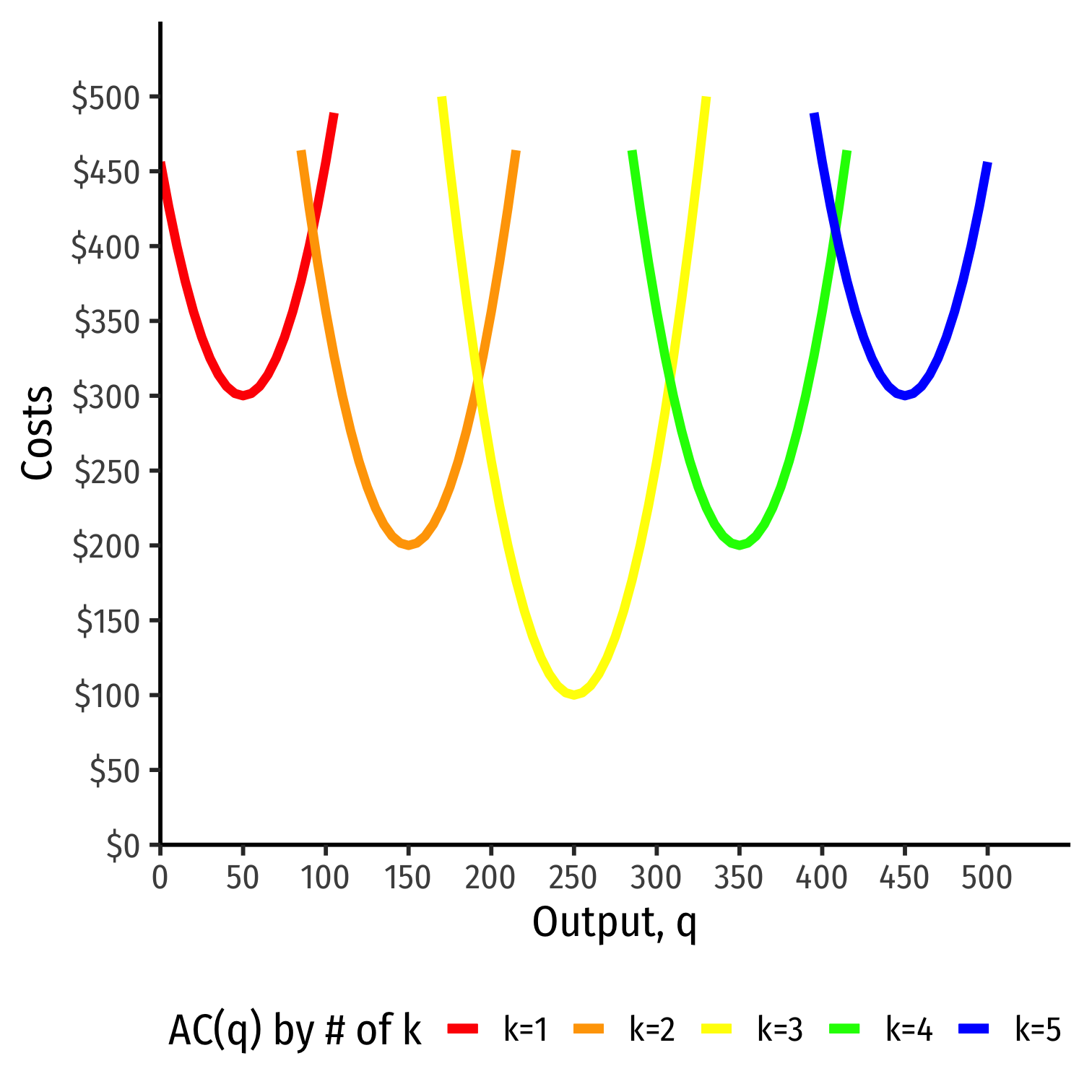
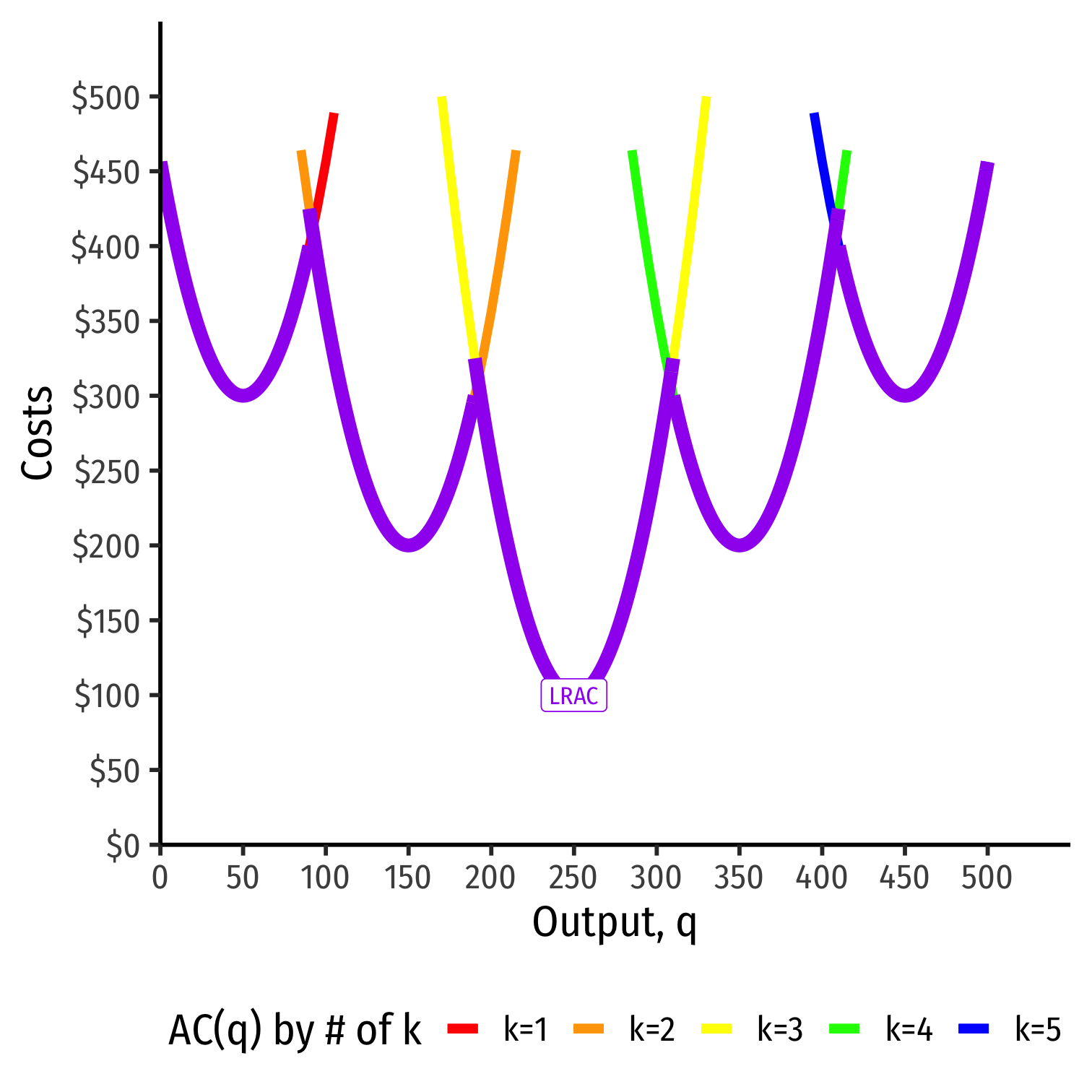
Average Cost in the Long Run

  • Long run: firm can choose k (factories, locations, etc)

  • Separate short run average cost (SRAC) curves for each amount of k potentially chosen

  • Long run average cost (LRAC) curve "envelopes" the lowest (optimal) parts of all the SRAC curves!

"Subject to producing the optimal amount of output, choose l and k to minimize cost"

Long Run Costs & Scale Economies I

  • Further properties about costs based on scale economies of production:

  • Economies of scale: costs fall with output

    • AFC>AVC(q)

  • Diseconomies of scale: costs rise with output

    • AFC<AVC(q)

  • Constant economies of scale: costs don't change with output

    • Firm at minimum average cost

Long Run Costs & Scale Economies I

  • Note economies of scale ≠ returns to scale!

  • Returns to Scale (last class): a technological relationship between inputs & output

  • Economies of Scale (this class): an economic relationship between output and average costs

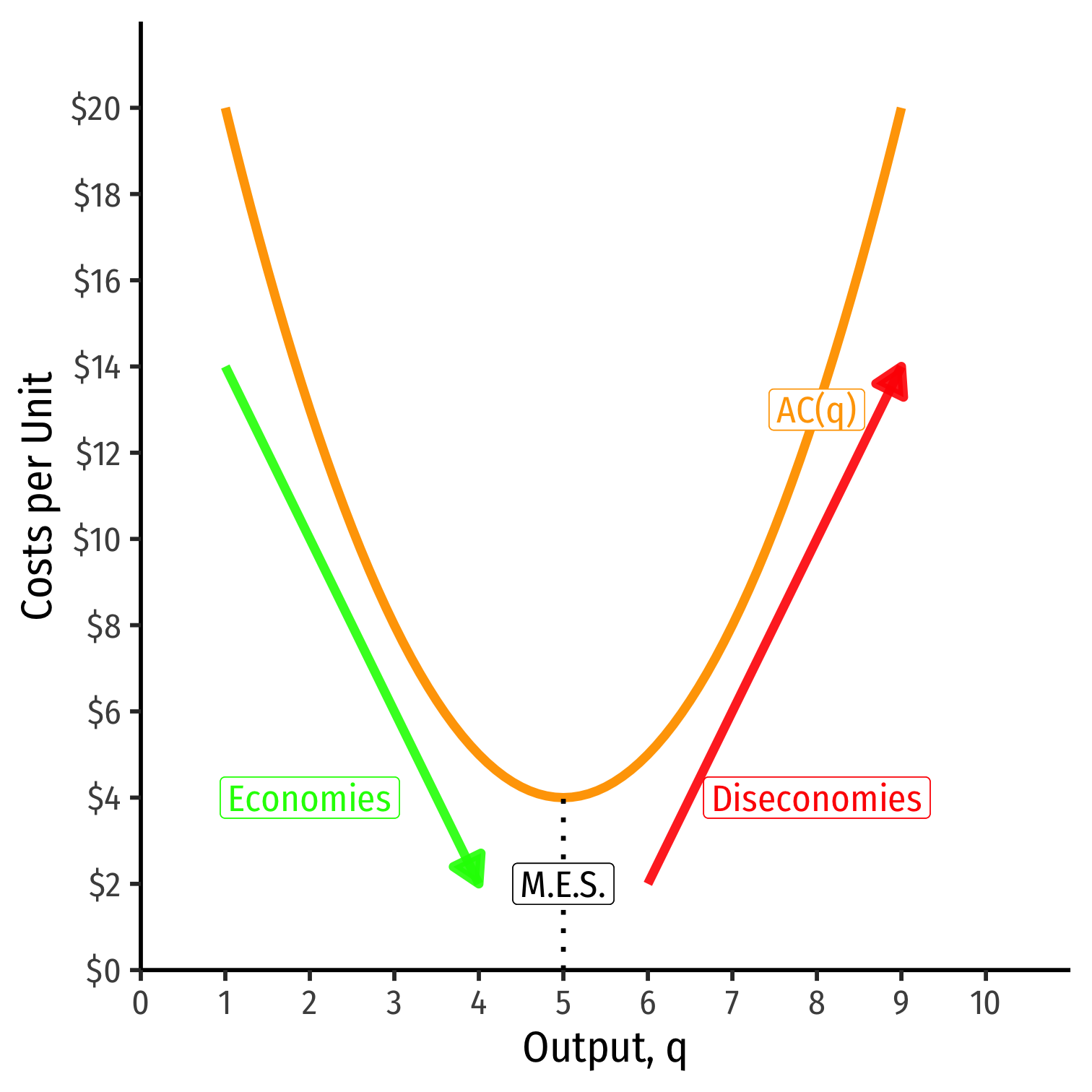
Long Run Costs & Scale Economies II

  • Minimum Efficient Scale: q with the lowest AC(q)

  • Economies of Scale: ↑q, ↓AC(q)

  • Diseconomies of Scale: ↑q, ↑AC(q)

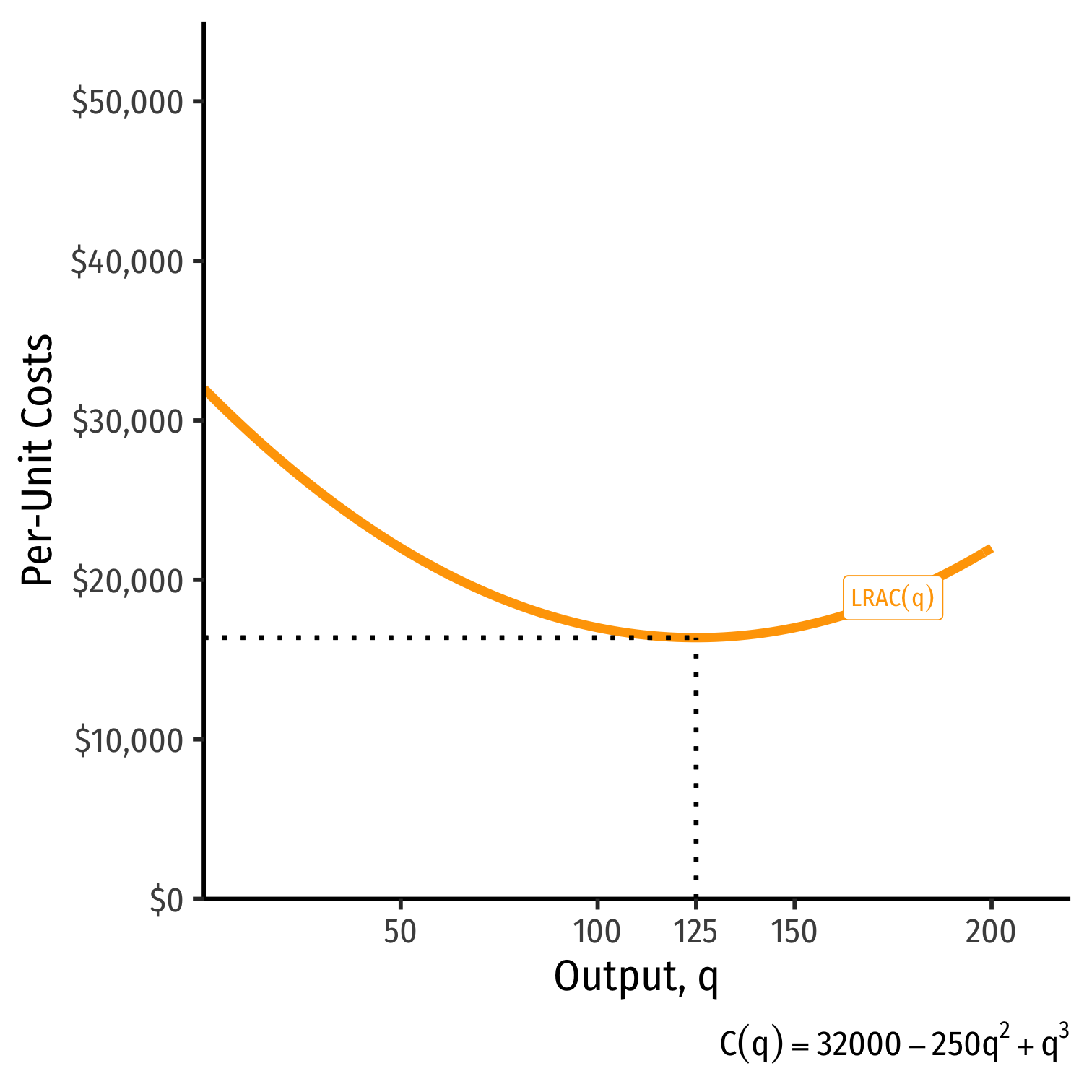
Long Run Costs and Scale Economies: Example

Example: A firm's long run cost structure is as follows:

LRC(q)=32000q−250q2+q3LRMC(q)=32000−500q+3q2

  1. At what levels of output will the firm face economies of scale and diseconomies of scale? (Hint: This firm has a U-shaped LRAC.)

Long Run Costs and Scale Economies: Example

Recall: The Firm's Two Problems

  • 1st Stage: firm's profit maximization problem:

  1. Choose: < output >

  2. In order to maximize: < profits >

  • We'll cover this later...first we'll explore:

  • 2nd Stage: firm's cost minimization problem:

  1. Choose: < inputs >

  2. In order to minimize: < cost >

  3. Subject to: < producing the optimal output >

  • Minimizing costs ⟺ maximizing profits

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow