+ - 0:00:00
Notes for current slide
Notes for next slide

4.6 — Contestable Markets & Wrap Up

ECON 306 · Microeconomic Analysis · Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microF20
microF20.classes.ryansafner.com

Game Theory: Some Generalizations

Game Theory: Some Generalizations

There's a lot more to game theory than a one-shot prisoners' dilemma:

  • one shot vs. repeated game

  • discrete vs. continuous strategies

  • perfect vs. incomplete vs. and asymmetric information

  • simultaneous vs. sequential game

  • See my game theory course for more (likely taught next in Fall 2021)

Solution Concepts

  • We use "solution concepts" to allow us to predict an equilibrium of a game

  • Nash Equilibrium is the primarly solution concept

    • Note it has many variants depending on if games are sequential vs. simultaneous, perfect vs. imperfect information, etc.

Solution Concepts: Nash Equilibrium

  • Recall, Nash Equilibrium: no players want to change their strategy given what everyone else is playing
    • All players are playing a best response to each other

Solution Concepts: Nash Equilibrium

  • Important about Nash equilibrium:

  • N.E. ≠ the "best" or optimal outcome

    • Recall the Prisoners' Dilemma!

  • Game may have multiple N.E.

  • Game may have no N.E. (in "pure" strategies)

Example: Coordination Game

  • A Coordination Game
    • No dominant strategies

Example: Coordination Game

  • Two Nash equilibria: (A,A) and (B,B)
    • Either just as good
    • Coordination is most important

Example: Coordination Game

  • Two general methods to solve for Nash equilibria:

1) Cell-by-Cell Inspection: look in each cell, does either player want to deviate?

  • If no: a Nash equilibrium
  • If yes: not a Nash equilibrium

Example: Coordination Game

  • Two general methods to solve for Nash equilibria:

2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?

  • Ties are allowed
  • Any cell where both players are playing a best response is a Nash Equilibrium

Example: Coordination Game

Player 1's best responses

  • Two general methods to solve for Nash equilibria:

2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?

  • Ties are allowed
  • Any cell where both players are playing a best response is a Nash Equilibrium

Example: Coordination Game

Player 2's best responses

  • Two general methods to solve for Nash equilibria:

2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?

  • Ties are allowed
  • Any cell where both players are playing a best response is a Nash Equilibrium

Example: Coordination Game

N.E.: each player is playing a best response

  • Two general methods to solve for Nash equilibria:

2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?

  • Ties are allowed
  • Any cell where both players are playing a best response is a Nash Equilibrium

A Change in the Game

  • Two Nash equilibria again: (A,A) and (B,B)

  • But here (A,A) ≻ (B,B)!

A Change in the Game

  • Path Dependence: early choices may affect later ability to choose or switch

  • Lock-in: the switching cost of moving from one equilibrium to another becomes prohibitive

  • Suppose we are currently in equilibrium (B,B)

  • Inefficient lock-in:

    • Standard A is superior to B
    • But too costly to switch from B to A

Contestable Markets

Is Monopoly a Nash Equilibrium?

  • Now that we understand Nash equilibrium...

  • Are outcomes of other market structures Nash equilibria?

Is Monopoly a Nash Equilibrium?

  • Now that we understand Nash equilibrium...

  • Are outcomes of other market structures Nash equilibria?

  • Perfect competition: no firm wants to raise or lower price given the market price ✓

Is Monopoly a Nash Equilibrium?

  • Monopolist maximizes π by setting q∗: MR=MC and p∗=Demand(q∗)

  • This is an equilibrium, but is it the only equilibrium?

  • We've assumed just a single player in the model

  • What about potential competition?

Contestable Markets I

  • Model the market as an entry game, with two players:

  1. Incumbent which sets its price pI

  2. Entrant decides to stay out or enter the market, setting its price pE

  • Price competition between 2 firms with similar products ⟹ consumers buy only from firm with lower price

Contestable Markets II

  • Suppose firms have costs of C(q)=cqMC(q)=c

  • If Incumbent sets pI>c, then Entrant would enter and set pE=pI−ϵ (for arbitrary ϵ>0)

Contestable Markets II

  • Suppose firms have costs of C(q)=cqMC(q)=c

  • If Incumbent sets pI>c, then Entrant would enter and set pE=pI−ϵ (for arbitrary ϵ>0)

    • Incumbent would forsee this, and try to price lower than pE
    • undercutting continues until...

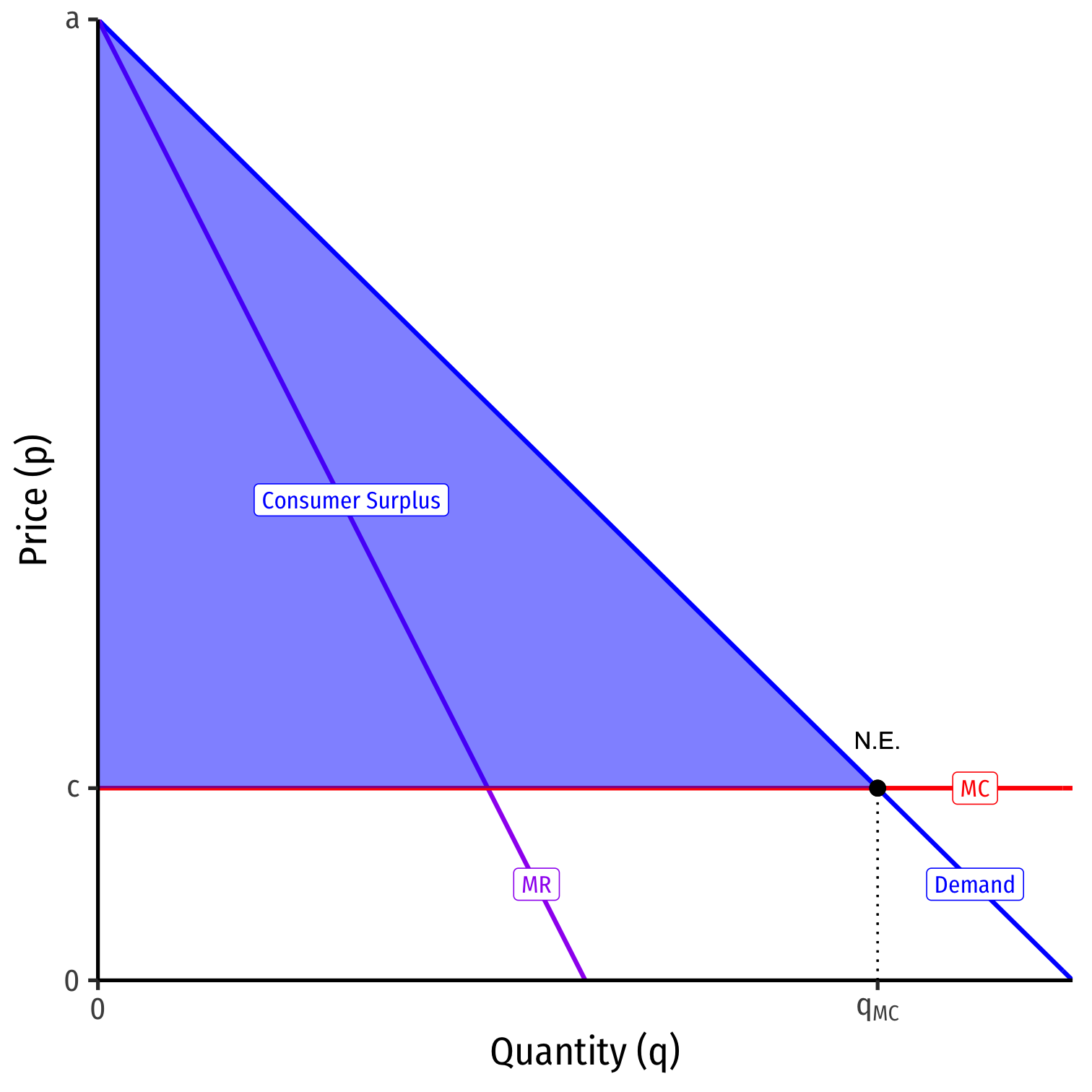
Contestable Markets II

  • Nash Equilibrium: incumbent sets pI=c, no entry

  • A market with a single firm, but the competitive outcome!

    • p∗=MC, π=0
    • competitive q∗
    • max Consumer Surplus, no DWL

Contestable Markets II

  • What if the entrant has higher costs than the incumbent: cE>cI?

Contestable Markets II

  • What if the entrant has higher costs than the incumbent: cE>cI?

  • Nash equilibrium: incumbent sets pI=pE−ϵ

    • arbitrary ϵ>0

  • Entrant stays out

  • One firm, but not a worst case monopoly

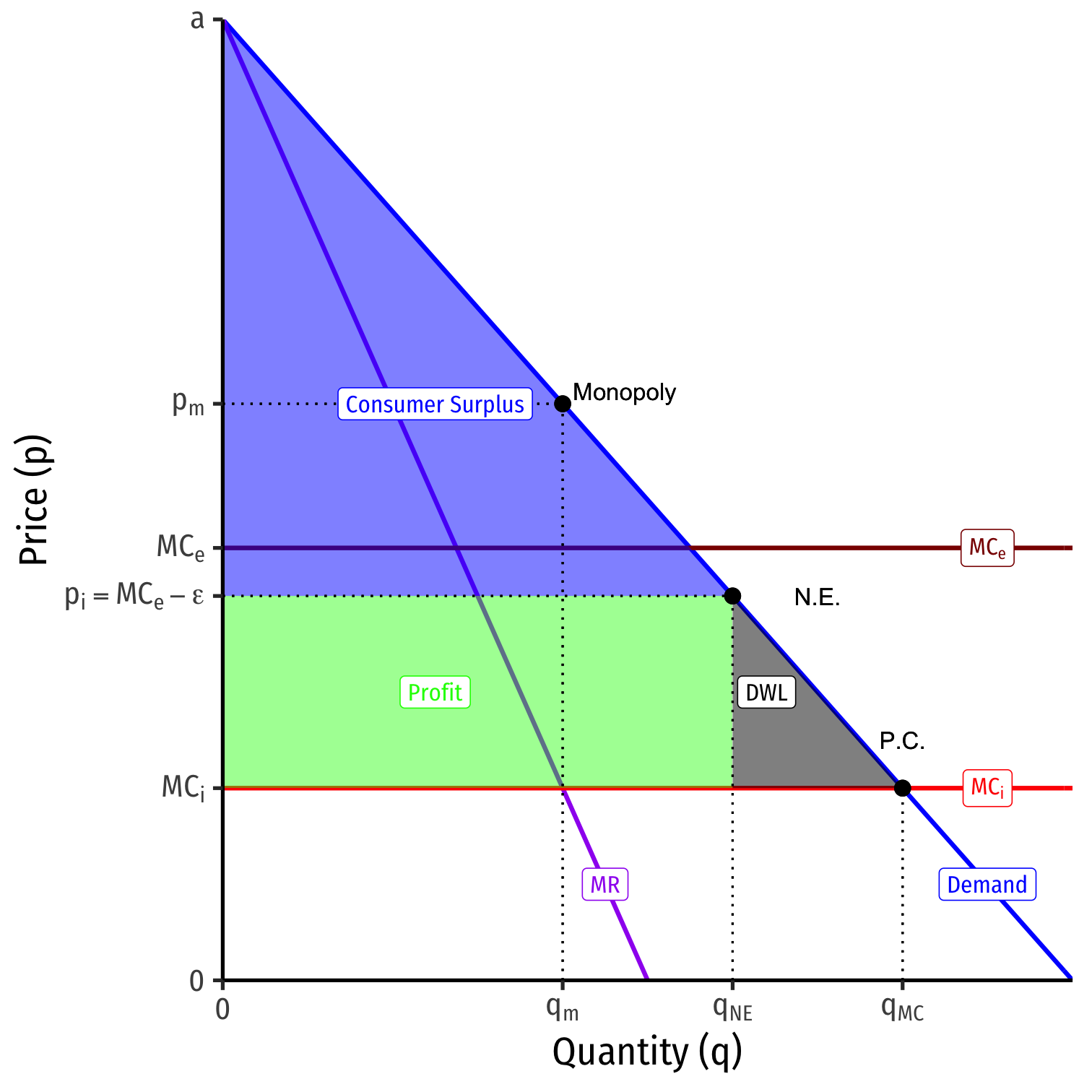
Contestable Markets II

  • What if the entrant has higher costs than the incumbent: cE>cI?

  • Nash equilibrium: incumbent sets pI=pE−ϵ

    • arbitrary ϵ>0

  • Entrant stays out

  • One firm, but not a worst case monopoly

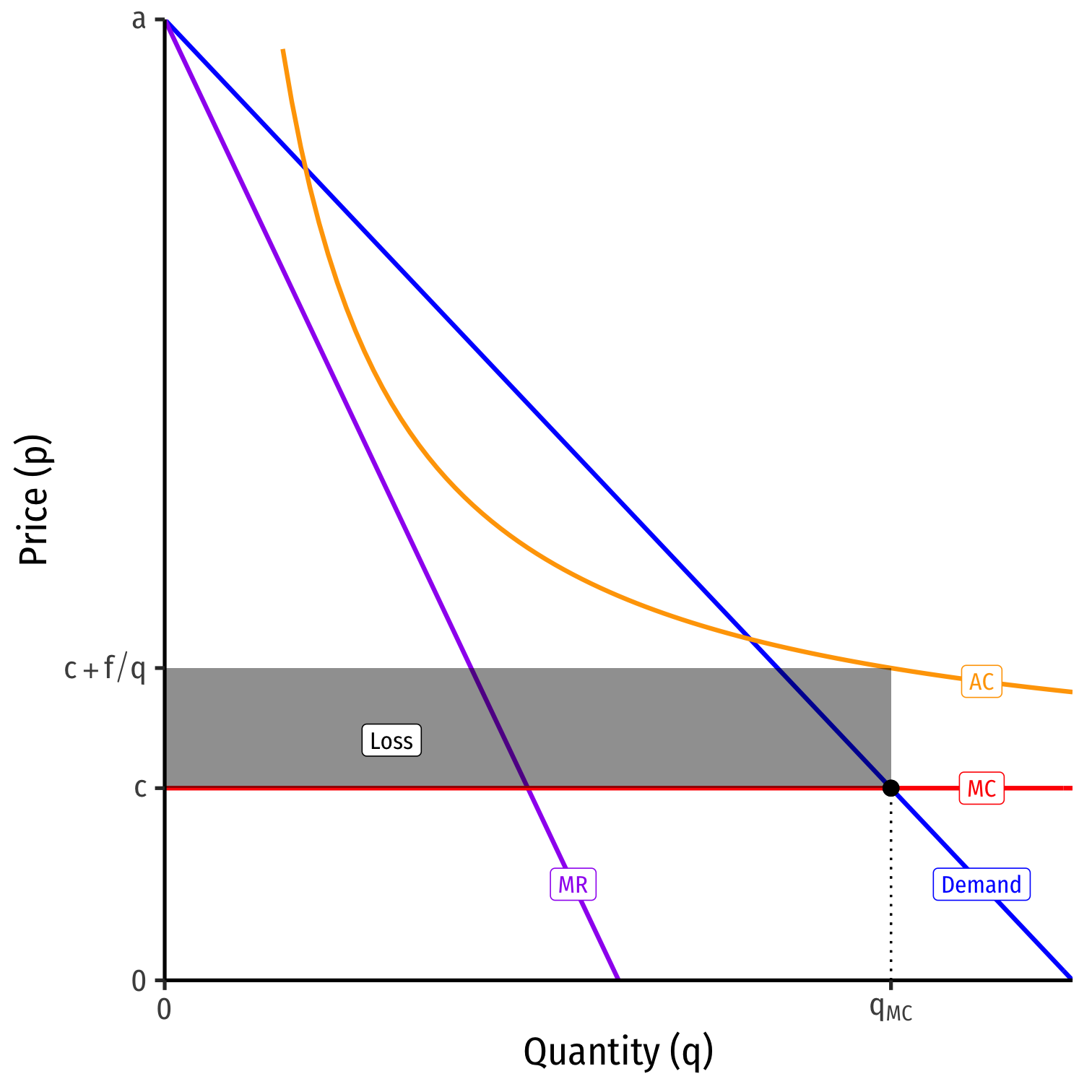
Contestable Markets III

  • What if there are fixed costs, f?

C(q)=cq+fMC(q)=cAC(q)=c+fq

  • With high enough f, Economies of scale may prevent marginal cost pricing from a being profitable Nash Equilibrium

πp=MC=−fq<0

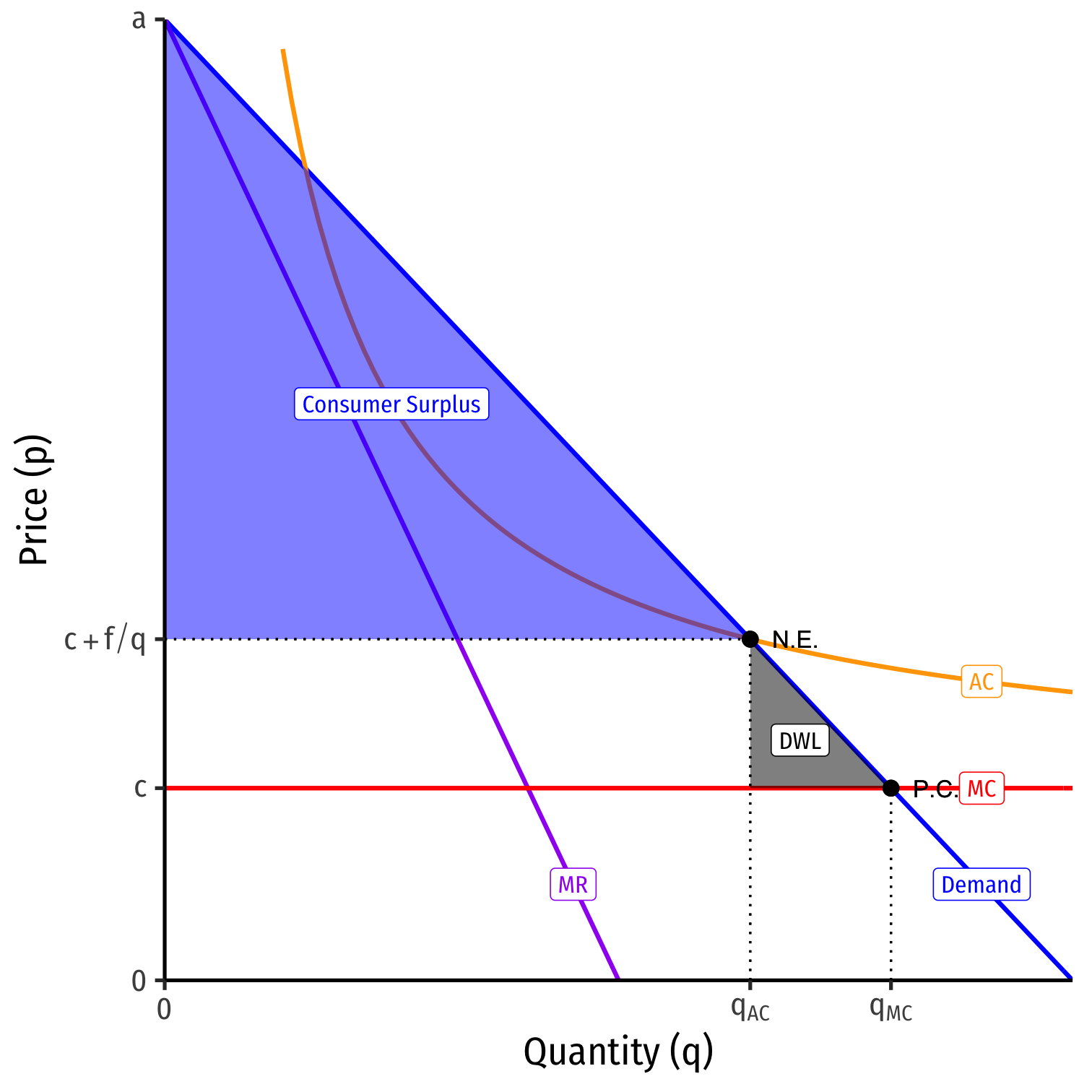
Contestable Markets IV

  • Nash equilibrium: Incumbent prices at pI=AC earns π=0

  • Entrant stays out

  • Again, single firm, but not a monopoly

    • no profits
    • not allocatively efficient, p>MC, some DWL

Contestable Markets: Recap

  • Markets are contestable if:

    1. There are no barriers to entry or exit
    2. Firms have similar technologies (i.e. similar cost structure)
    3. There are no sunk costs

  • Economies of scale need not be inconsistent with competitive markets (as is assumed) if they are contestable

  • Generalizes "prefect competition" model in more realistic way, also game-theoretic

Contestable Markets: Summary

William Baumol

(1922--2017)

"This means that...an incumbent, even if he can threaten retaliation after entry, dare not offer profit-making opportunities to potential entrants because an entering firm can hit and run, gathering in the available profits and departing when the going gets rough."

Baumol, William, J, 1982, "Contestable Markets: An Uprising in the Theory of Industry Structure," American Economic Review, 72(1): 1-15

Implications for Competition

  • Regulation & antitrust (once) focus(ed) on number of firms

    • "Count the number of firms, if it's 1, it's a monopoly!"

  • Perfect competition as "gold standard", only market arrangement that is socially efficient:

    • Allocatively efficient: p=MC, DWL=0
    • Productively efficient: p=ACmin

Implications for Competition

  • But number of firms is endogenous and can evolve over time!

    • Function of how firms mutually interact strategically

  • A more dynamic situation: firms respond over time

Implications for Competition

  • Perfect competition not the only socially efficient market-structure

    • Small number of firms (including 1) may be efficient if they are contestable

  • Regulation and antitrust should consider whether a market is contestable, not just the number of firms

    • Free entry
    • No sunk costs

Implications for Competition

  • Firms engaging in egregious monopolistic behavior (↓q, ↑p, p>MC, π>0) largely persist because of barriers to entry

    • Attempts to make market uncontestable

  • Business activities or political dealings with the goal to raise cE>cI

    • ower your own costs, or raise your rivals'!

Monopoly Or Contestable Market?

Contestable Markets

"Of far greater concern to Microsoft is the competition from new and emerging technologies, some of which are currently visible and others of which certainly are not. This array of known, emerging, and wholly unknown competitors places enormous pressure on Microsoft to price competitively and innovate aggressively." (Schmalensee 1999)

Contestable Markets

So What's the Point of the Models?

  • In perfect competition (model):

    • price-taking firms set price equal to marginal cost
    • long run economic profits are zero
    • allocative efficiency: consumer and producer surplus maximized

  • This is a tendency only because of free entry and exit

So What's the Point of the Models?

  • Don't judge real markets by their similarity to the perfect competition model

  • Judge them more on their level of contestability, ease of potential entry

So What's the Point of the Models?

"...In that Empire, the Art of Cartography attained such Perfection that the map of a single Province occupied the entirety of a City, and the map of the Empire, the entirety of a Province. In time, those Unconscionable Maps no longer satisfied, and the Cartographers Guilds struck a Map of the Empire whose size was that of the Empire, and which coincided point for point with it. The following Generations, who were not so fond of the Study of Cartography as their Forebears had been, saw that that vast Map was Useless..."

Jorge Luis Borges, 1658, On Exactitude in Science

Economics Uses, but Is Not Limited to, Math

The Two Major Models of Economics as a “Science”

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

The Two Major Models of Economics as a “Science”

Optimization

  • Agents have objectives they value

  • Agents face constraints

  • Make tradeoffs to maximize objectives within constraints

Equilibrium

  • Agents compete with others over scarce resources

  • Agents adjust behaviors based on prices

  • Stable outcomes when adjustments stop

Economics Is Broader Than You Think

Game Theory: Some Generalizations

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow