+ - 0:00:00
Notes for current slide
Notes for next slide

4.1 — Modeling Market Power

ECON 306 · Microeconomic Analysis · Fall 2020

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microF20
microF20.classes.ryansafner.com

Outline

Market Power

Marginal Revenue

Price Elasticity & Price Mark Up

Profit Maximization Rules, Redux

Market Power

Imperfect Competition

Imperfect Competition

Imperfect Competition

Imperfect Competition

Competitive Markets, Recap

  • In a competitive market, we modeled firms as “price-takers” since there were so many of them selling identical products

    • Had to charge market price, could choose optimal q∗ to maximize π

  • Marginal cost pricing, which is allocatively efficient for society

    • p=MC
    • MSB=MSC

  • In the long-run, free entry and exit caused prices to equal (average & marginal) costs and pushed economic profits to zero

Market Power

Adam Smith

1723-1790

“People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices,” (Book I, Chapter 2.2).

Smith, Adam, 1776, An Enquiry into the Nature and Causes of the Wealth of Nations

Market Power vs. Competition

  • All sellers would like to raise prices and extract more revenue from consumers

  • Competition from other sellers (and potential entrants) drives prices to equal costs & economic profits to zero

  • If a firm in a competitive market raised p>MC(q), would lose all of its customers!

  • Market power: ability to raise p>MC(q) (and not lose all customers)

Modeling Firms with Market Power

  • Firms that have market power behave differently than firms in a competitive market

    • Today: understanding how to model that different behavior

  • Start with simple assumption of a single seller: monopoly

  • Next class:

    • causes of market power
    • consequences of market power

Modeling Firms with Market Power

  • A firm with market power is a “price-maker”

    • Can choose quantity q∗ and price p∗

  • We can also call it a “price-searcher”

    • Assuming the same objective as before, firms with market power must search for (q∗,p∗) that maximizes π

  • With a monopoly, we can safely ignore the effects that other firms have on the firm’s behavior (because there are none!)

    • Easiest starting point
    • Later we will have to complicate matters

The Monopolist's Problem

  • The monopolist’s profit maximization problem:

  1. Choose: < output and price: (q⋆,p⋆) >

  2. In order to maximize: < profits: π >

Marginal Revenues

Market Power and Revenues I

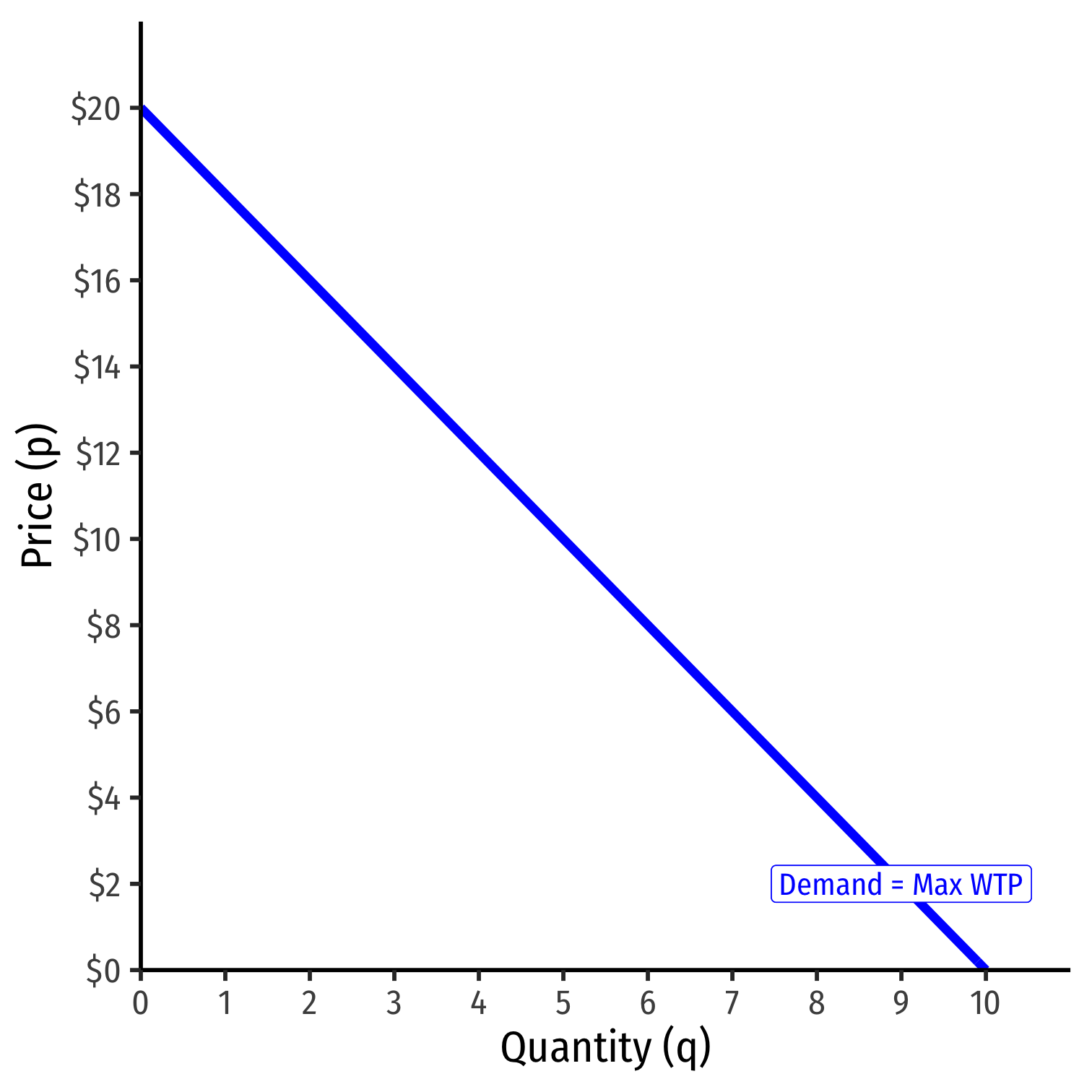
  • Firms are constrained by relationship between quantity and price that consumers are willing to pay

  • Market (inverse) demand describes maximum price consumers are willing to pay for a given quantity

  • Implications:

    • Even a monopoly can’t set a price “as high as it wants”
    • Even a monopoly can still earn losses!

Market Power and Revenues II

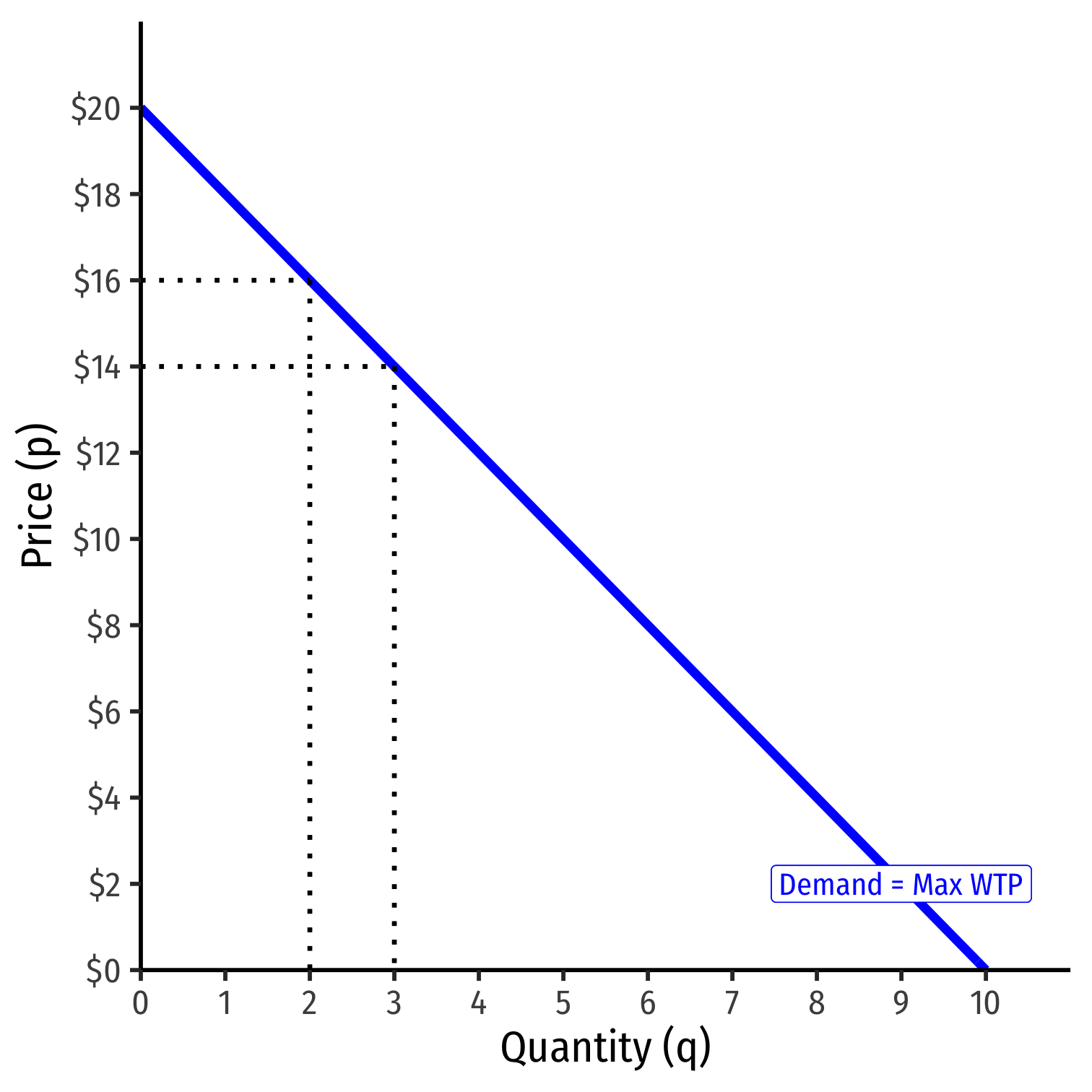
  • As firm chooses to produce more q, must lower the price on all units to sell them

Market Power and Revenues II

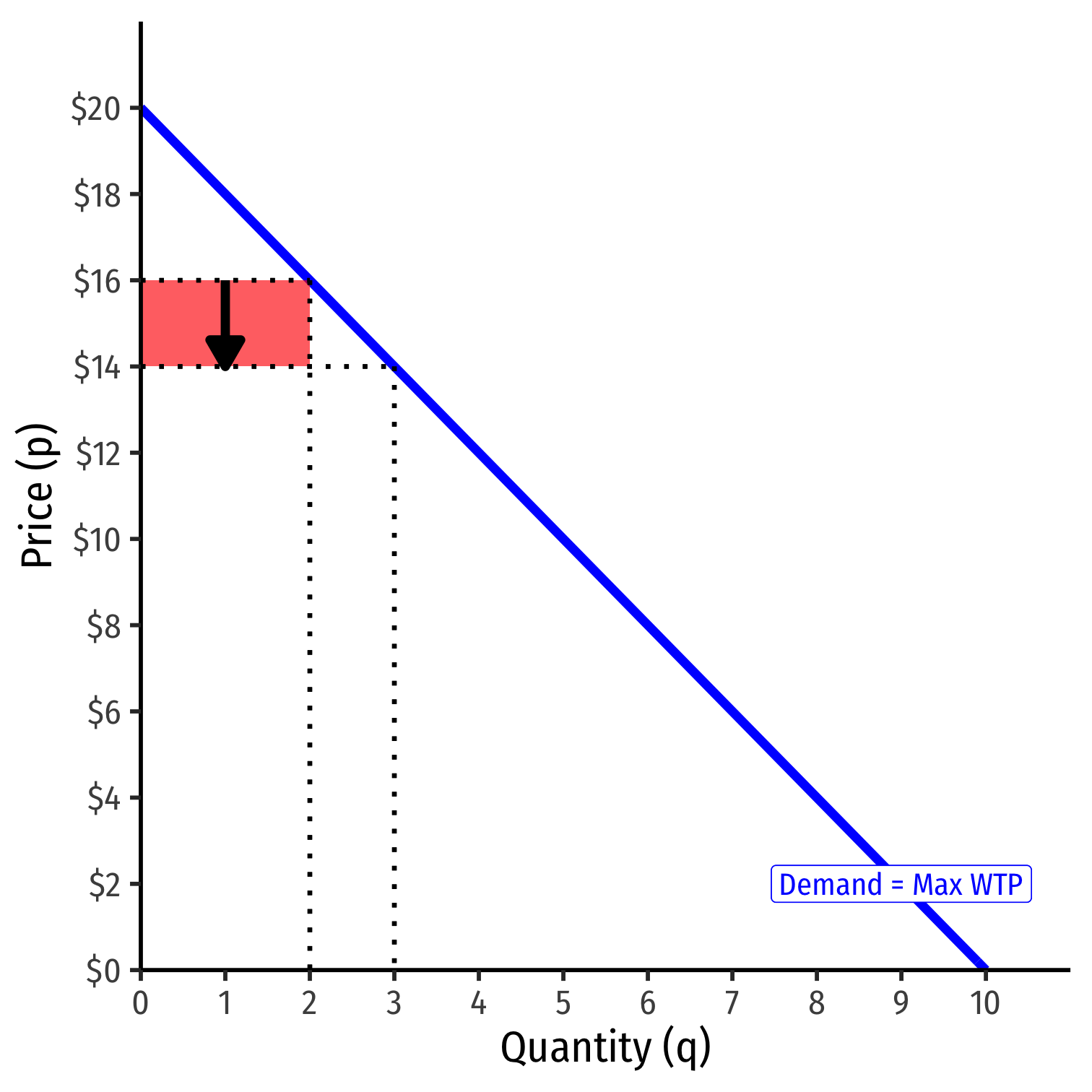
  • As firm chooses to produce more q, must lower the price on all units to sell them

  • Price effect: lost revenue from lowering price on all sales

Market Power and Revenues II

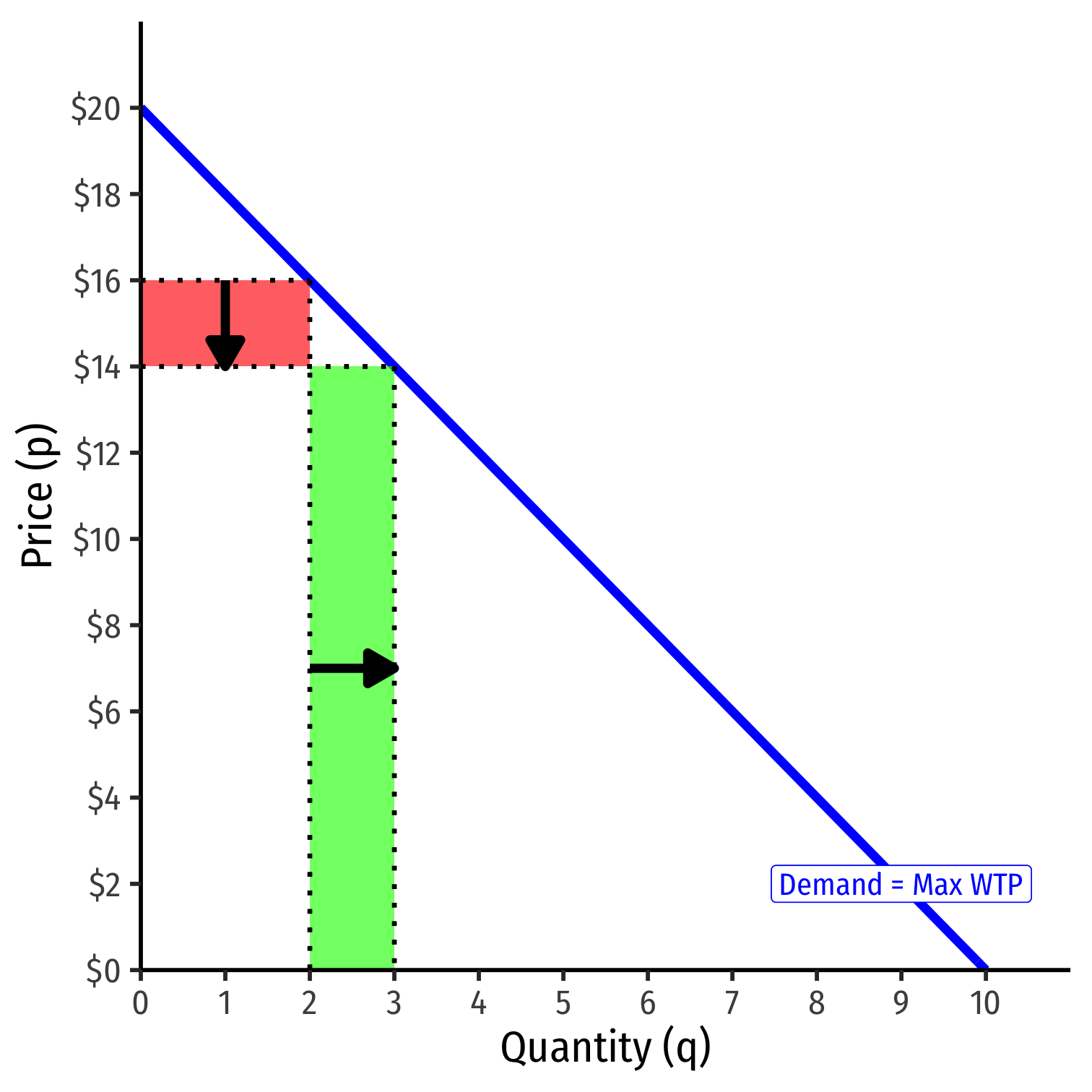
  • As firm chooses to produce more q, must lower the price on all units to sell them

  • Price effect: lost revenue from lowering price on all sales

  • Output effect: gained revenue from increase in sales

Marginal Revenue I

  • If a firm increases output, Δq, revenues would change by:

ΔR(q)=pΔq + qΔp

Marginal Revenue I

  • If a firm increases output, Δq, revenues would change by:

ΔR(q)=pΔq + qΔp

  • Output effect: increases number of units sold (Δq) times price p per unit

Marginal Revenue I

  • If a firm increases output, Δq, revenues would change by:

ΔR(q)=pΔq + qΔp

  • Output effect: increases number of units sold (Δq) times price p per unit

  • Price effect: lowers price per unit (Δp) on all units sold (q)

Marginal Revenue I

  • If a firm increases output, Δq, revenues would change by:

ΔR(q)=pΔq + qΔp

  • Output effect: increases number of units sold (Δq) times price p per unit

  • Price effect: lowers price per unit (Δp) on all units sold (q)

  • Divide both sides by Δq to get Marginal Revenue, MR(q):

ΔR(q)Δq=MR(q)=p+ΔpΔqq

Marginal Revenue I

  • If a firm increases output, Δq, revenues would change by:

ΔR(q)=pΔq + qΔp

  • Output effect: increases number of units sold (Δq) times price p per unit

  • Price effect: lowers price per unit (Δp) on all units sold (q)

  • Divide both sides by Δq to get Marginal Revenue, MR(q):

ΔR(q)Δq=MR(q)=p+ΔpΔqq

  • Compare: demand for a competitive firm is perfectly elastic: ΔpΔq=0, so we saw MR(q)=p!

Marginal Revenue II

  • If we have a linear inverse demand function of the form p=a+bq
    • a is the choke price (intercept)
    • b is the slope

Marginal Revenue II

  • If we have a linear inverse demand function of the form p=a+bq
    • a is the choke price (intercept)
    • b is the slope
  • Marginal revenue again is defined as: MR(q)=p+ΔpΔqq

Marginal Revenue II

  • If we have a linear inverse demand function of the form p=a+bq
    • a is the choke price (intercept)
    • b is the slope
  • Marginal revenue again is defined as: MR(q)=p+ΔpΔqq
  • Recognize that ΔpΔq=(riserun) is the slope, b,

Marginal Revenue II

  • If we have a linear inverse demand function of the form p=a+bq
    • a is the choke price (intercept)
    • b is the slope
  • Marginal revenue again is defined as: MR(q)=p+ΔpΔqq
  • Recognize that ΔpΔq=(riserun) is the slope, b,

MR(q)=p+(b)qMR(q)=(a+bq)+bqMR(q)=a+2bq

Marginal Revenue III

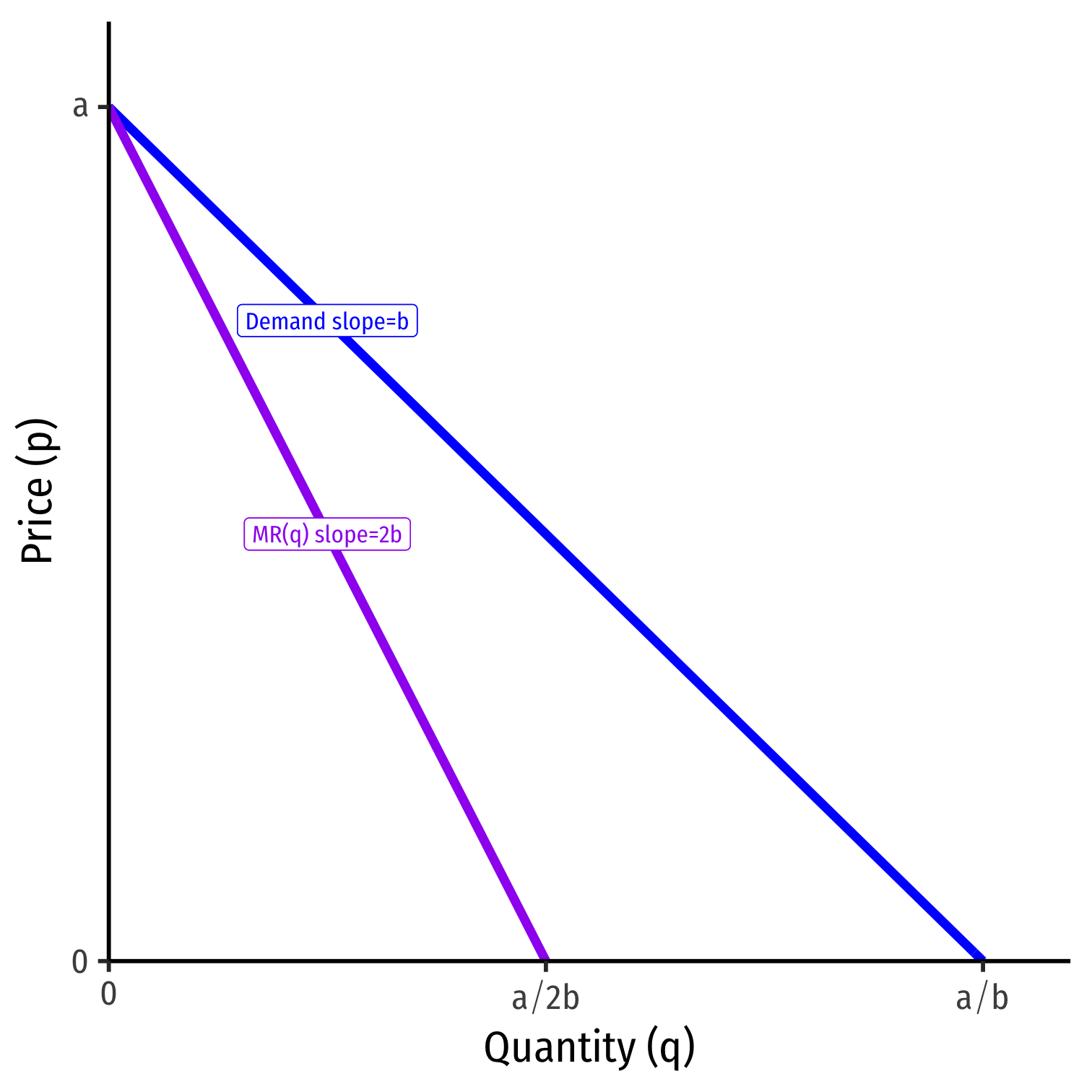
p(q)=a+bqMR(q)=a+2bq

  • Marginal revenue starts at same intercept as Demand (a) with twice the slope (2b)

  • Don’t forget the slopes (b) are always negative!

Marginal Revenue: Example

Example: Suppose the market demand is given by:

q=12.5−0.25p

  1. Find the function for a monopolist’s marginal revenue curve.

  2. Calculate the monopolist’s marginal revenue if the firm produces 6 units, and 7 units.

Price Elasticity & Price Mark Up

Revenues and Price Elasticity of Demand

Demand Price Elasticity MR(q) R(q)
|ϵ|>1 Elastic Positive Increasing
|ϵ|=1 Unit 0 Maximized
|ϵ|<1 Inelastic Negative Decreasing

  • Strong relationship between price elasticity of demand and revenues

  • Monopolists only produce where demand is elastic, with positive MR(q)!

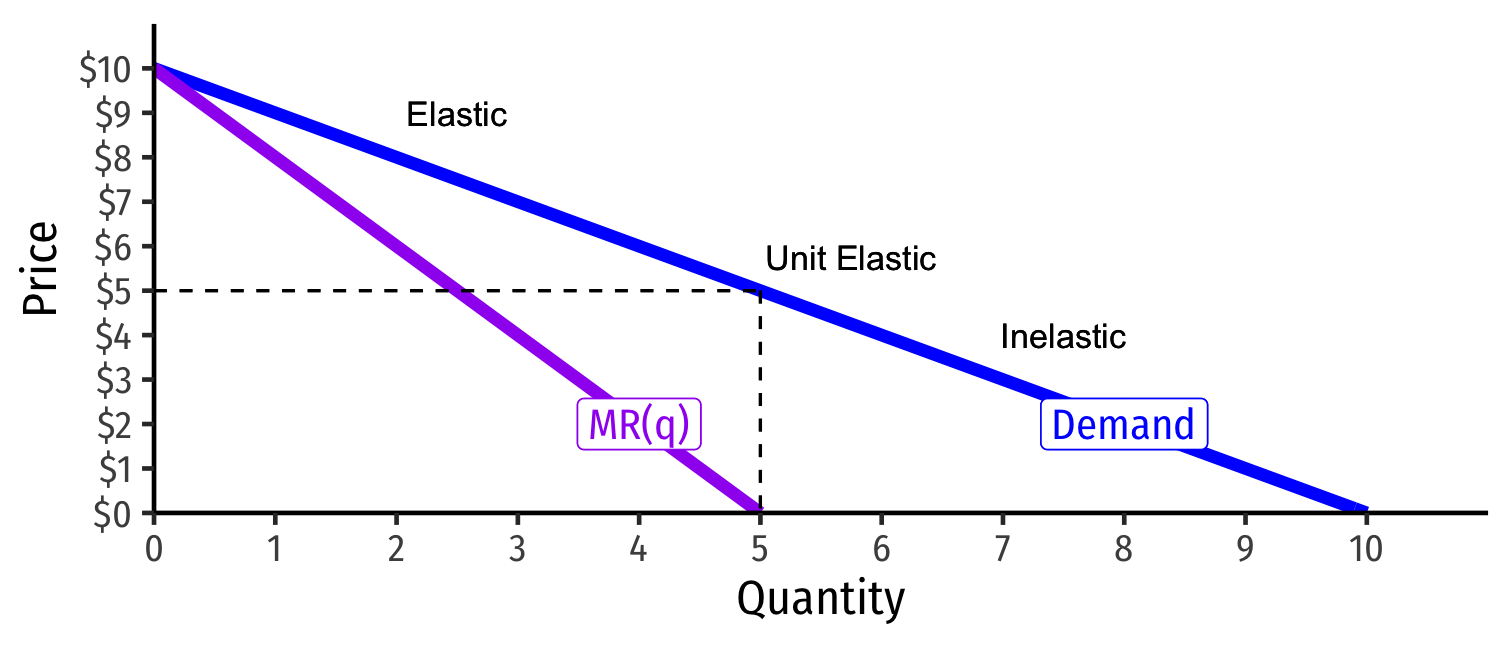
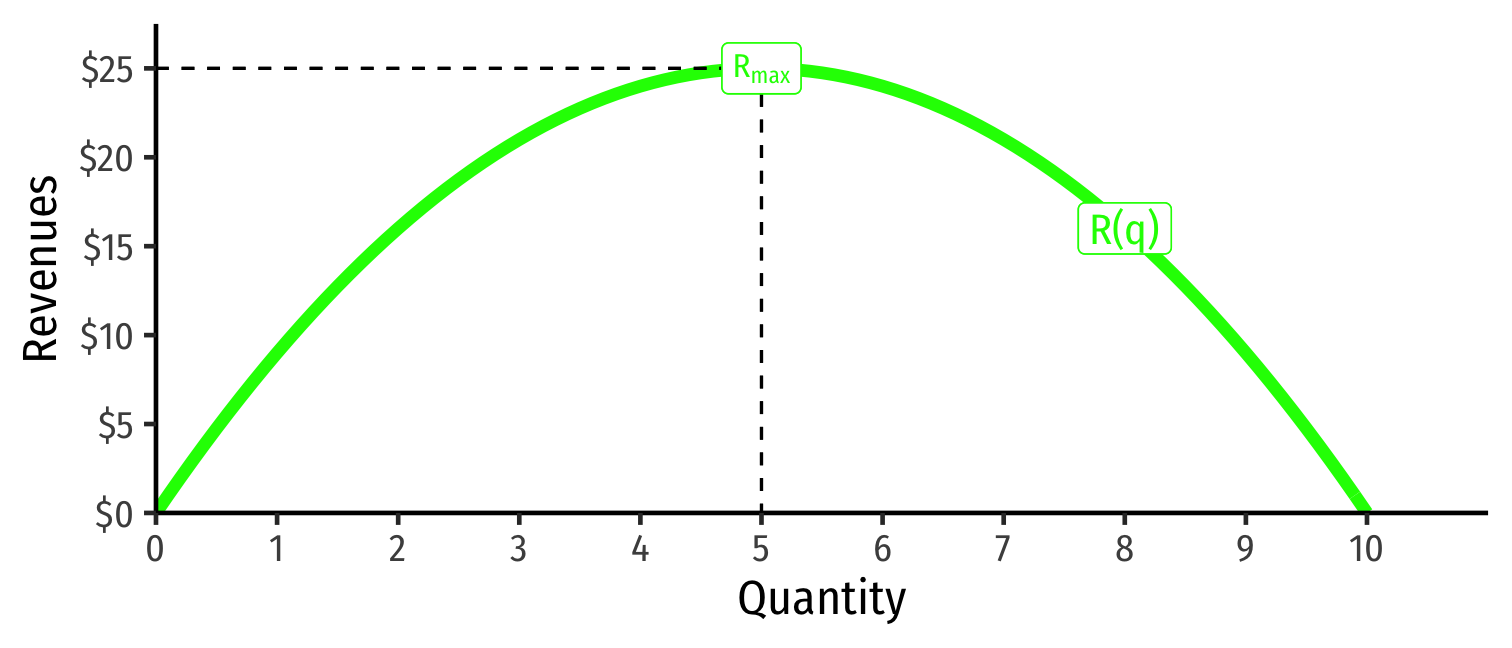
Market Power and Mark Up

  • Perfect competition: p=MC(q) (allocatively efficient)

  • Market power defined as firm(s)’ ability to raise mark up p>MC(q)

    • Even a monopolist is constrained by market demand

  • Size of markup depends on price elasticity of demand

    • ↓ price elasticity: ↑ markup

i.e. the less responsive to prices consumers are, the higher the price the firm can charge

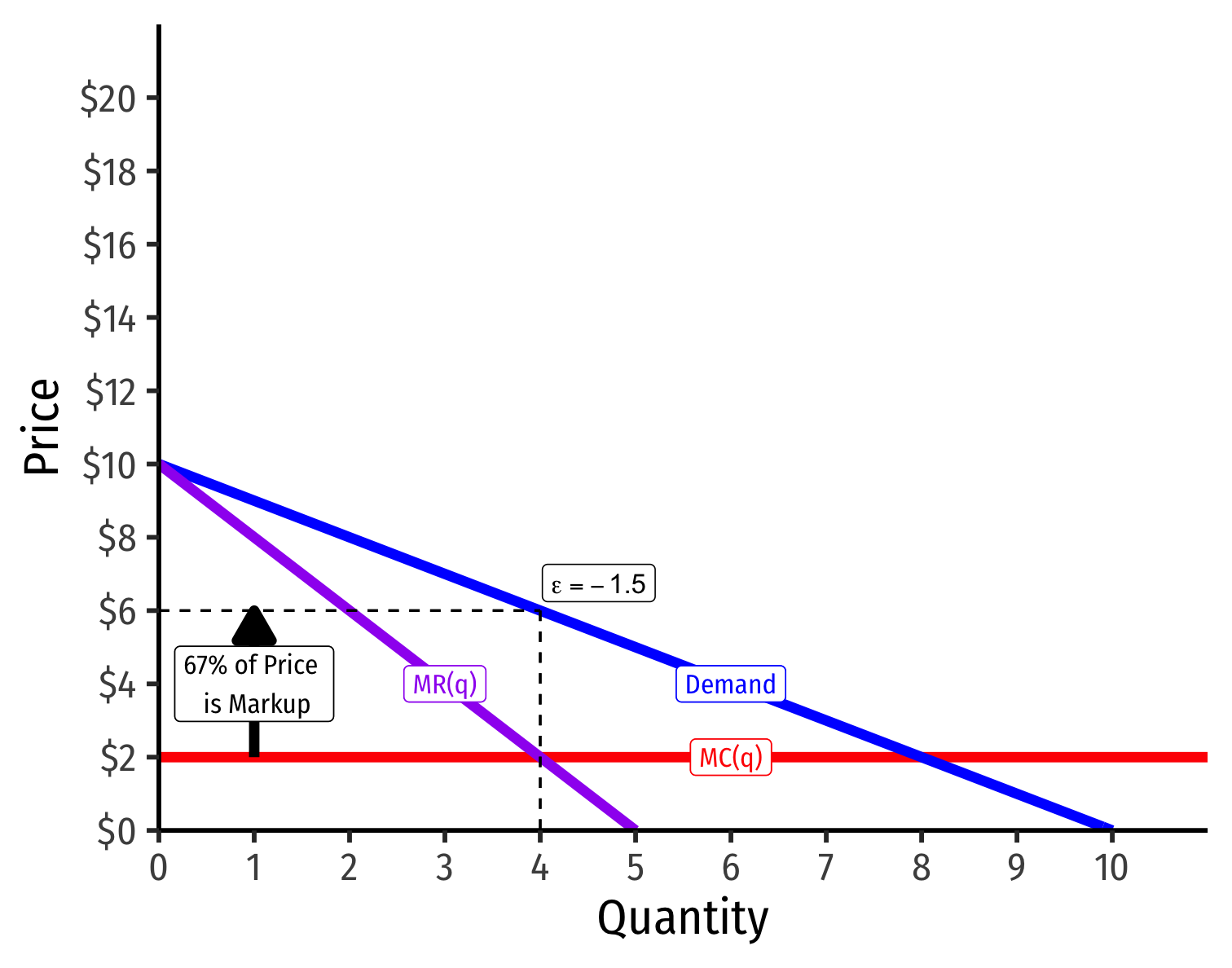
The Lerner Index and Inverse Elasticity Rule I

  • Lerner Index measures market power as % of firm's price that is markup above MC(q)

L=p−MC(q)p=−1ϵ

  • i.e. L×100% of firm's price is markup
  • L=0⟹ perfect competition
    • 0% of price is markup, since P=MC(q)
  • As L→1⟹ more market power
    • 100% of price is markup

See today's class notes for the derivation.

The Lerner Index and Inverse Elasticity Rule II

The more (less) elastic a good, the less (more) the optimal markup: L=p−MC(q)p=−1ϵ

Demand Less Elastic at p∗

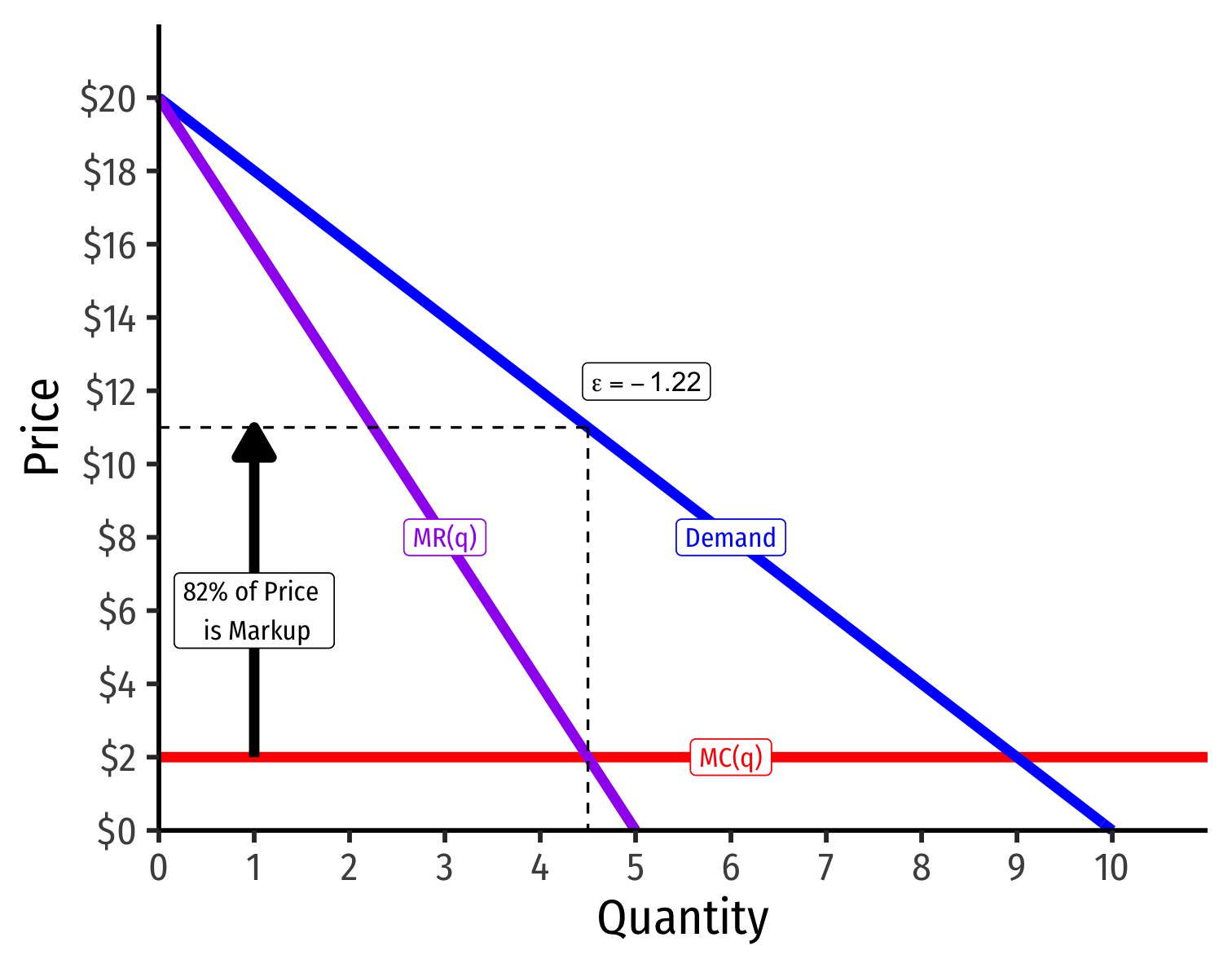
Demand More Elastic at p∗

Profit Maximization Rules, Redux

Visualizing Total Profit As R(q)-C(q)

  • π(q)=R(q)−C(q)

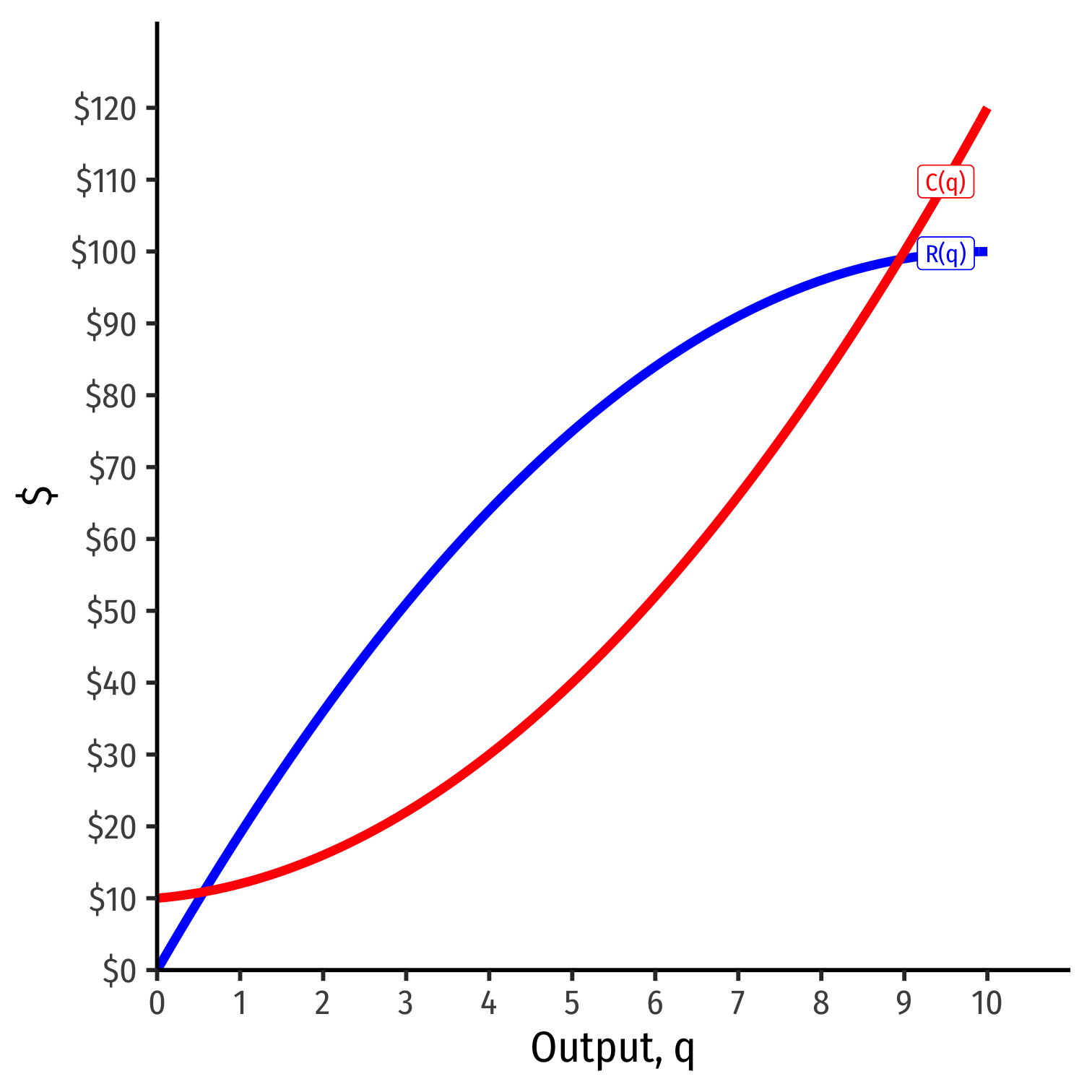
Visualizing Total Profit As R(q)-C(q)

  • π(q)=R(q)−C(q)

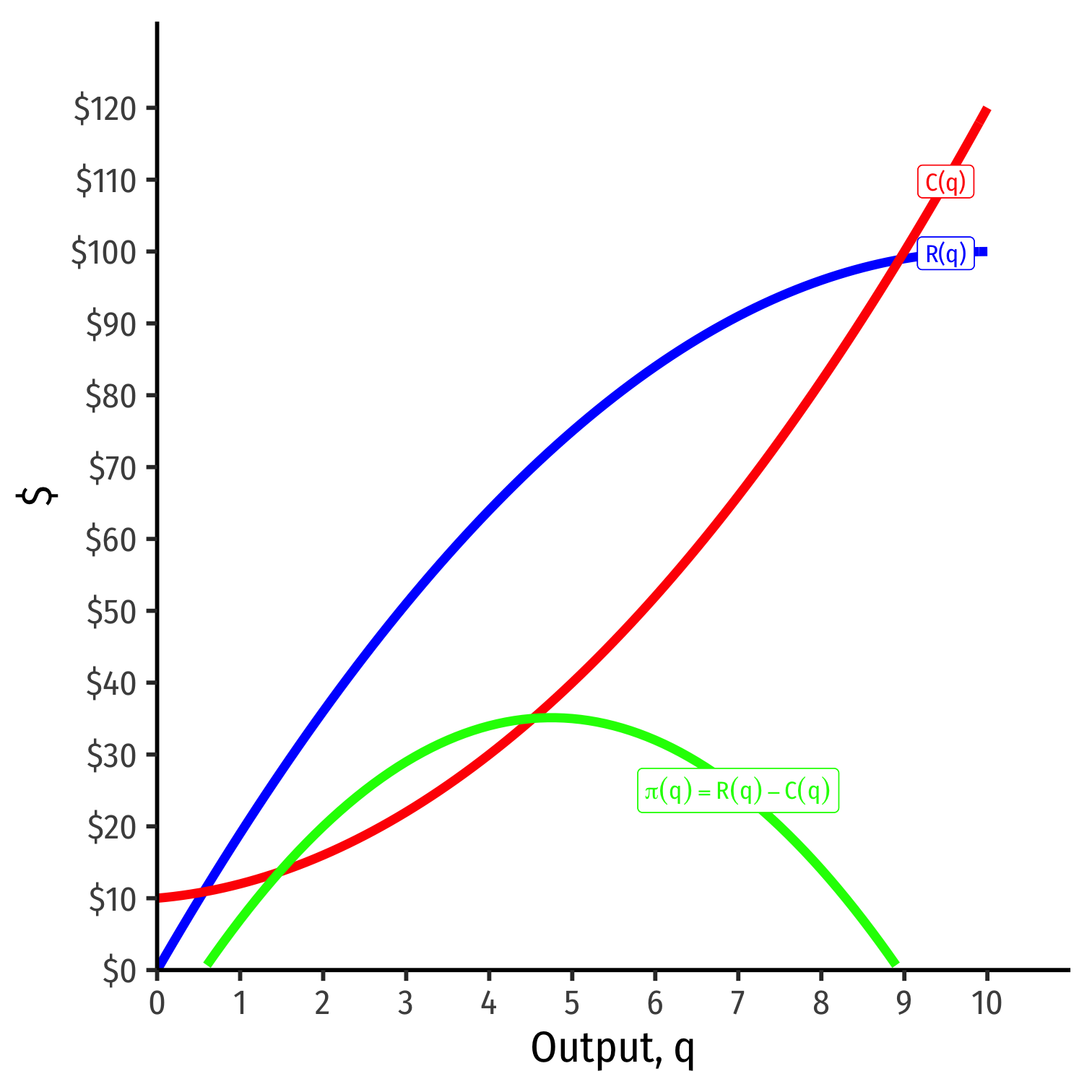
Visualizing Total Profit As R(q)-C(q)

  • π(q)=R(q)−C(q)

  • Graph: find q∗ to max π⟹q∗ where max distance between R(q) and C(q)

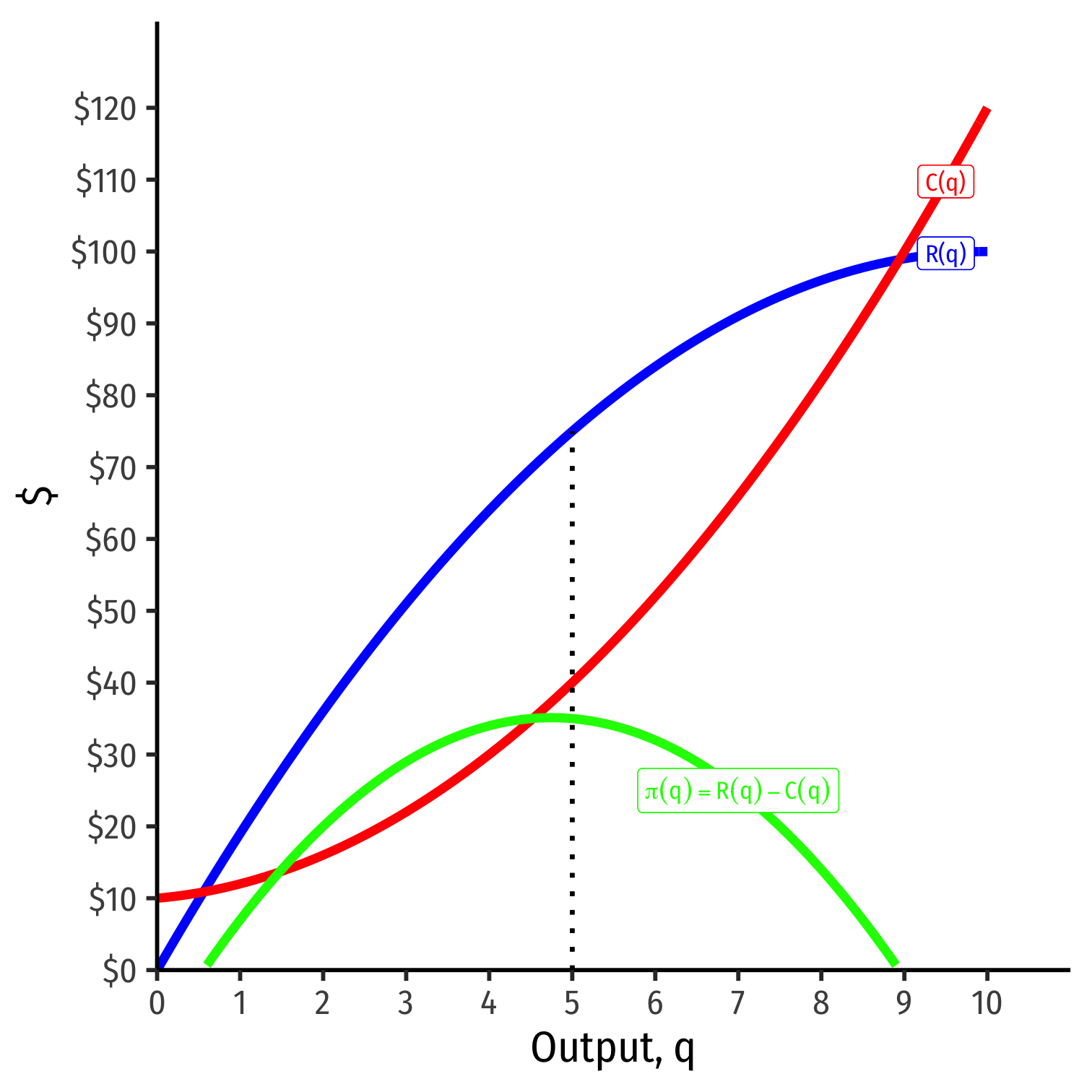
Visualizing Total Profit As R(q)-C(q)

  • π(q)=R(q)−C(q)

  • Graph: find q∗ to max π⟹q∗ where max distance between R(q) and C(q)

  • Slopes must be equal: MR(q)=MC(q)

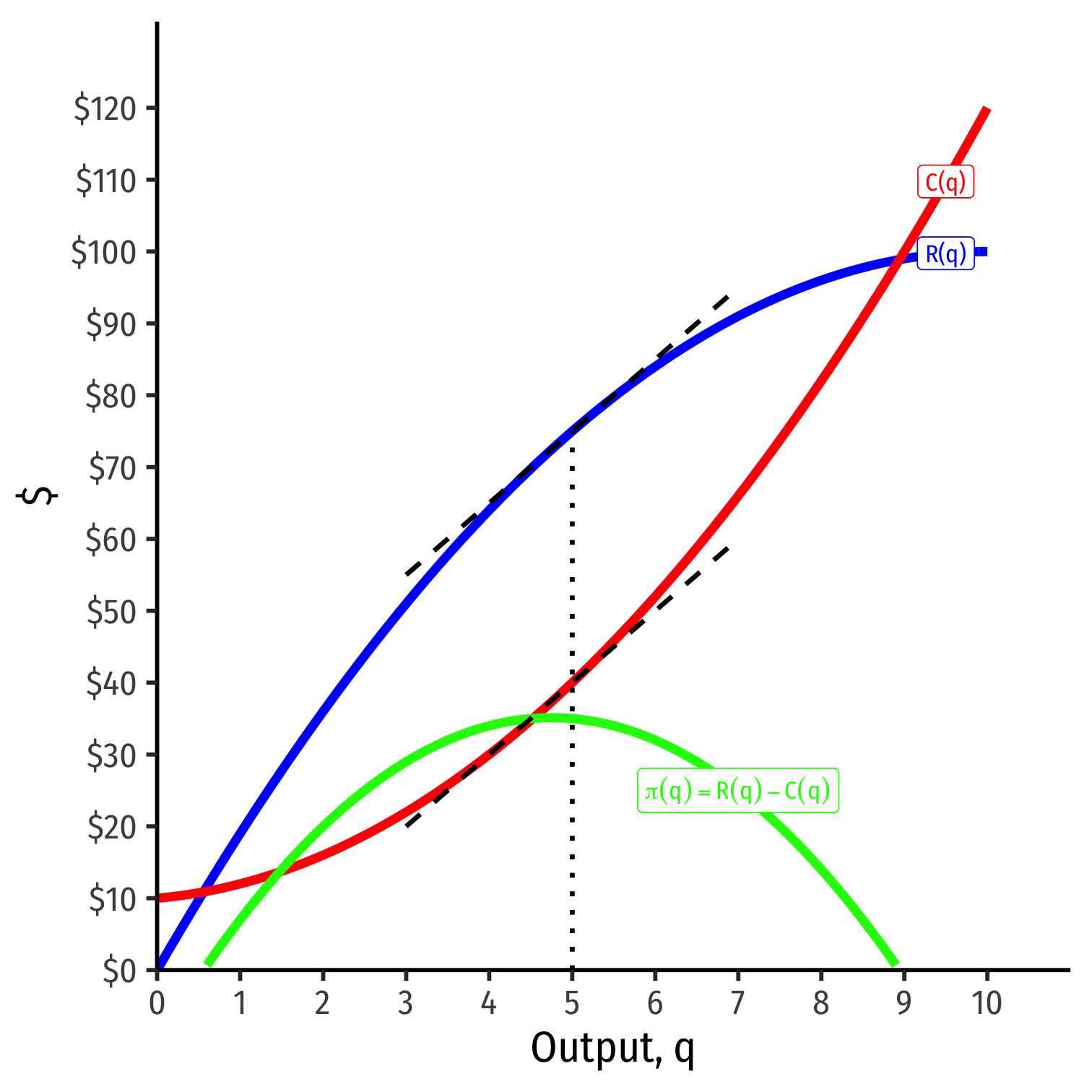
Visualizing Total Profit As R(q)-C(q)

  • π(q)=R(q)−C(q)

  • Graph: find q∗ to max π⟹q∗ where max distance between R(q) and C(q)

  • Slopes must be equal: MR(q)=MC(q)

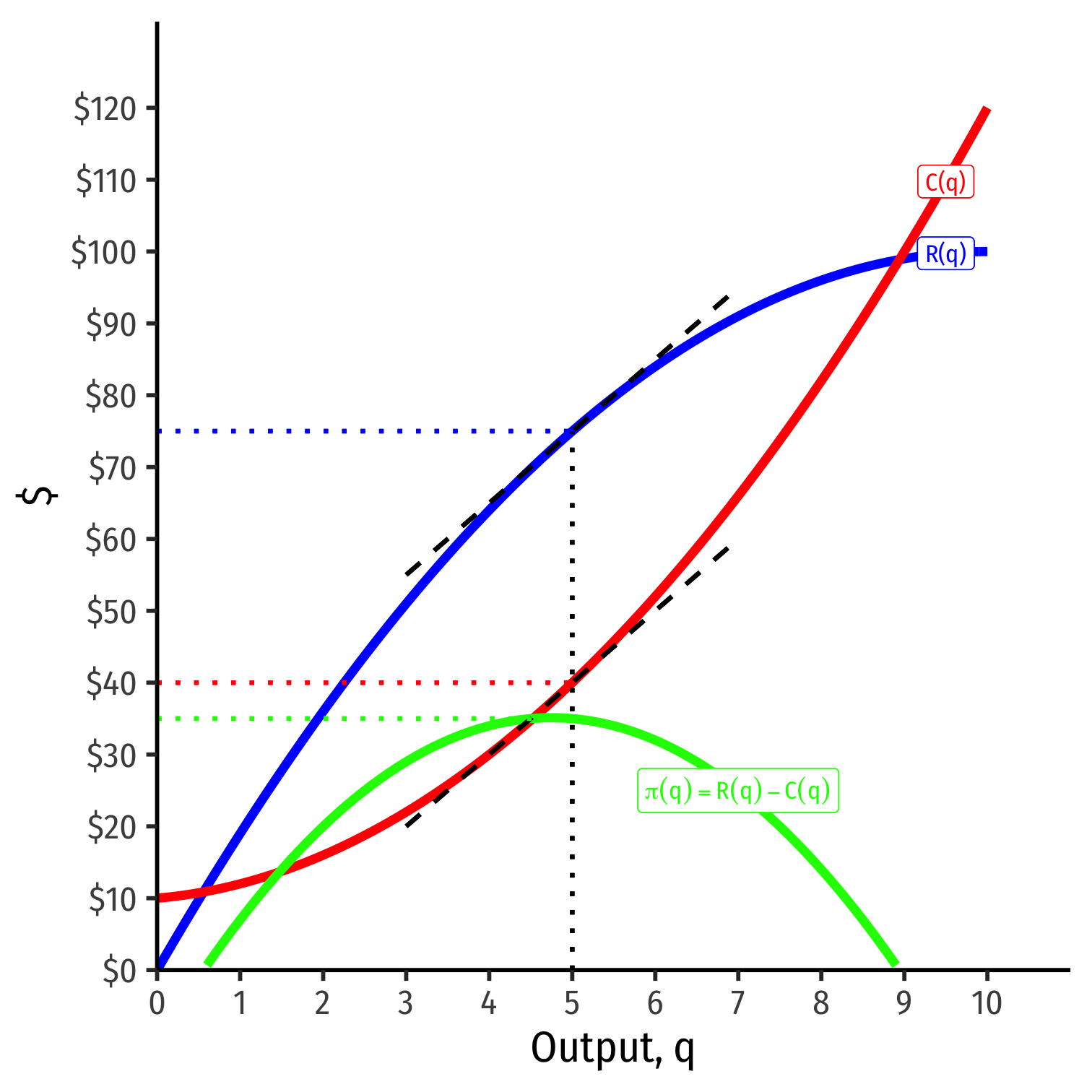
  • At q∗=5:
    • R(q)=75
    • C(q)=40
    • π(q)=35

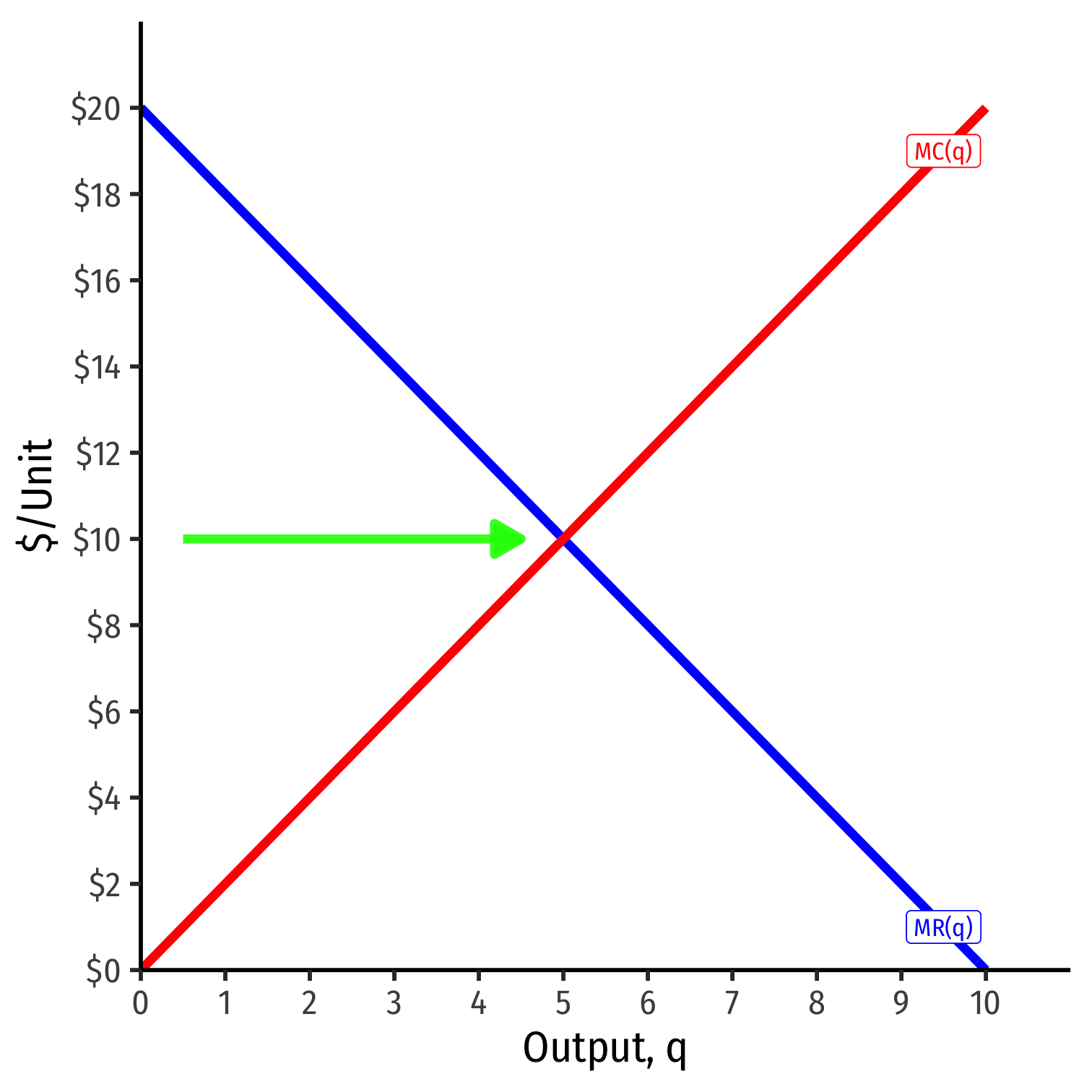
Visualizing Marginal Profit As MR(q)-MC(q)

  • At low output q<q∗, can increase π by producing more

  • MR(q)>MC(q)

Visualizing Marginal Profit As MR(q)-MC(q)

  • At high output q>q∗, can increase π by producing less

  • MR(q)<MC(q)

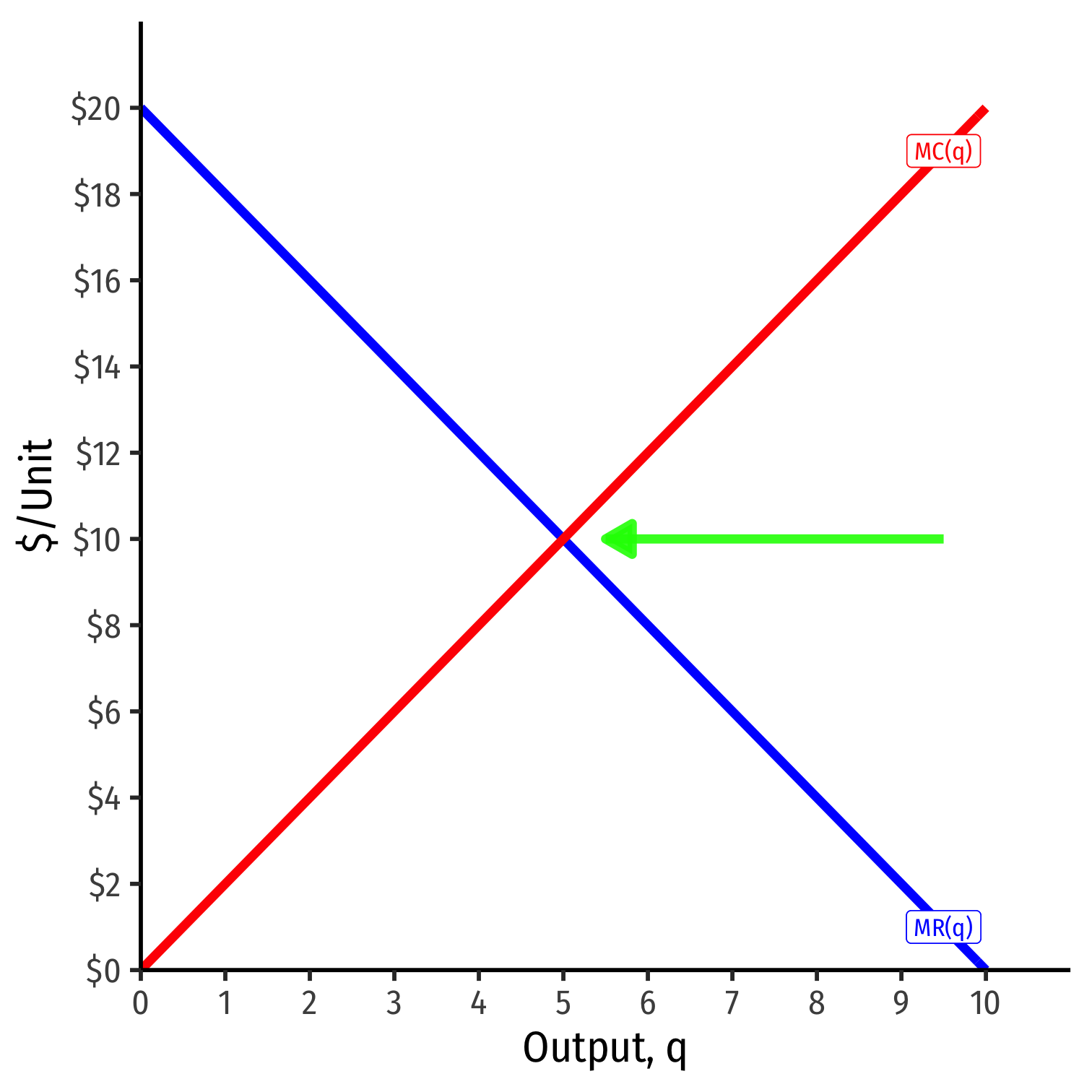
Visualizing Marginal Profit As MR(q)-MC(q)

  • π is maximized where MR(q)=MC(q)

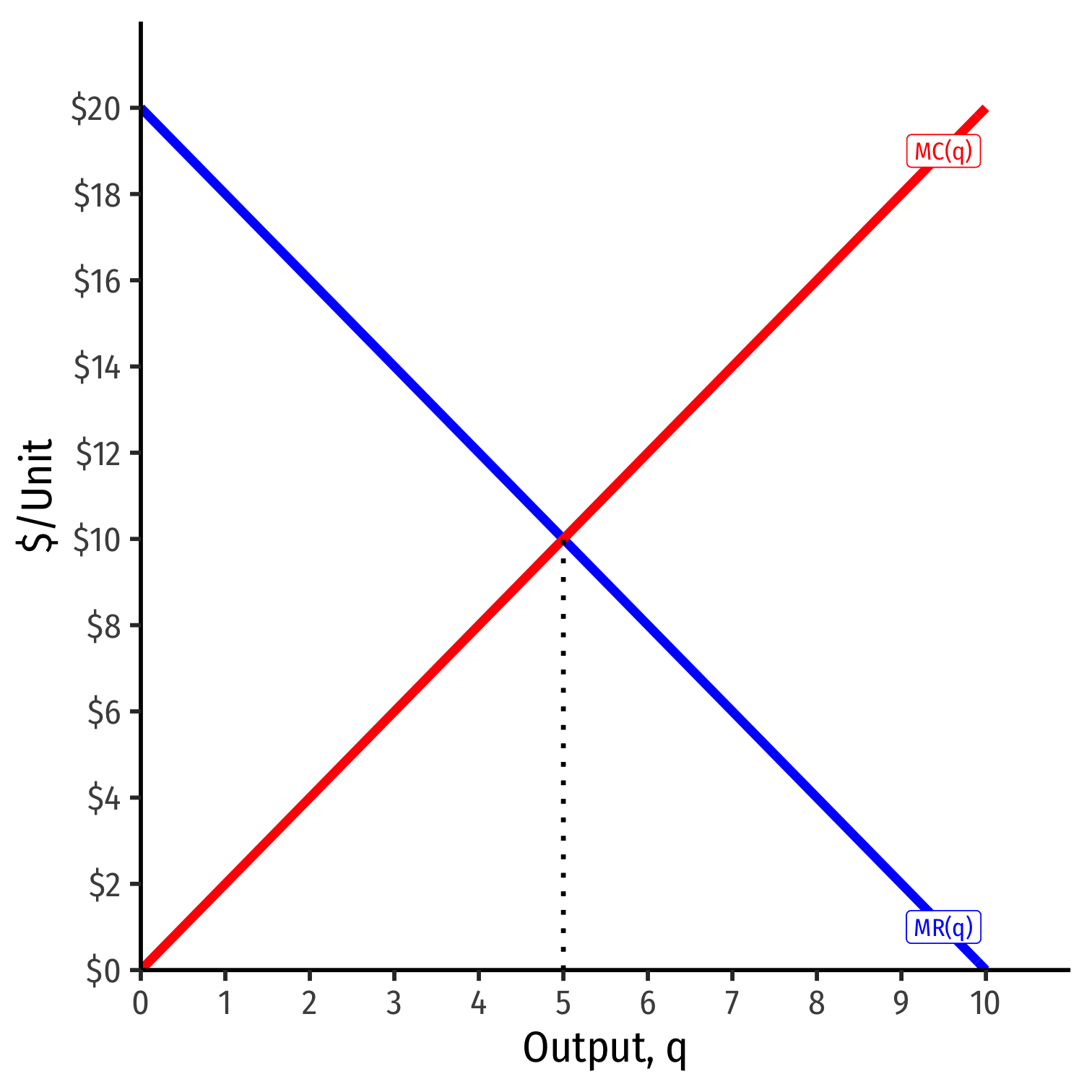
Profit-Maximizing Price and Quantity (Graph)

  • Profit-maximizing quantity is always q∗ where MR(q) = MC(q)

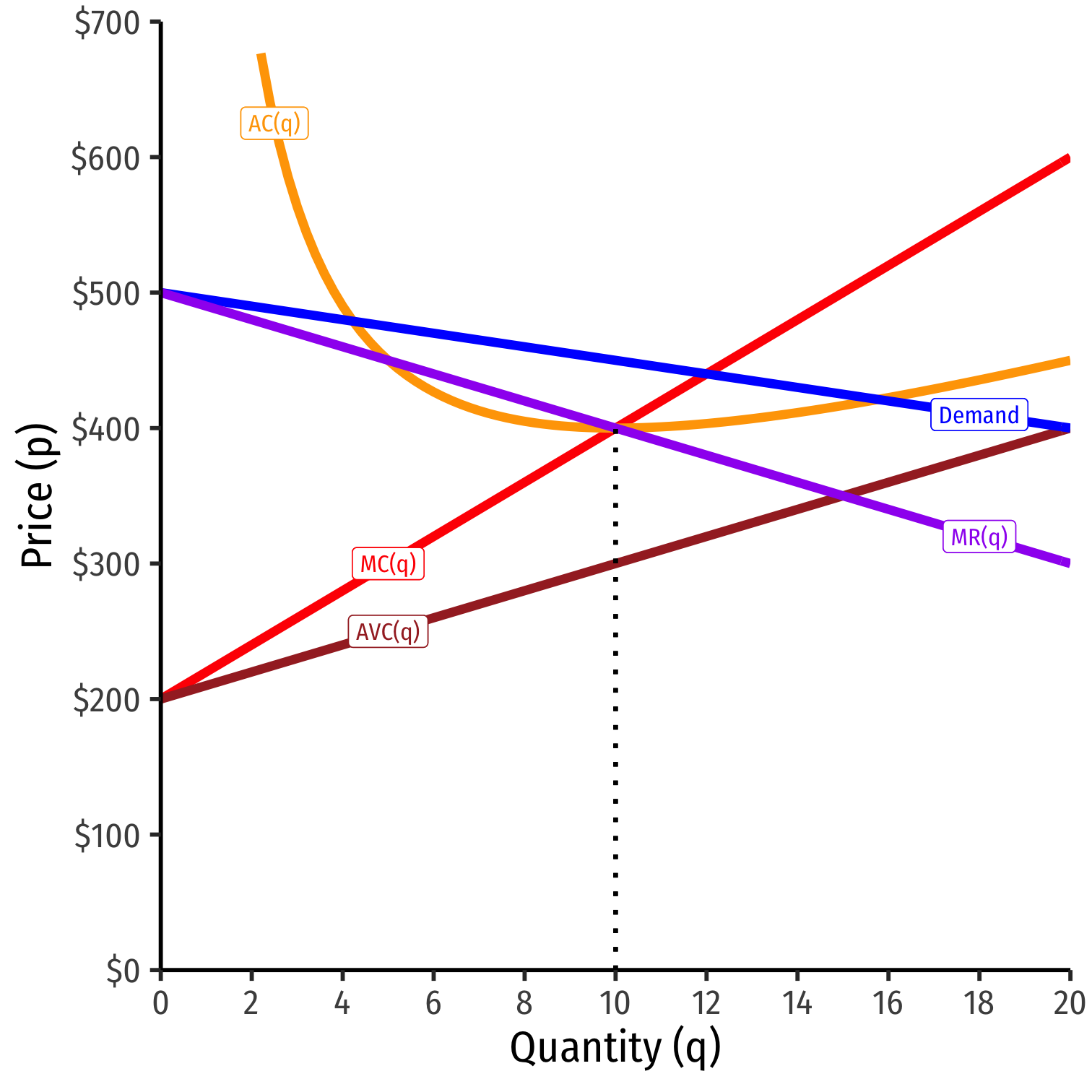
Profit-Maximizing Price and Quantity (Graph)

  • Profit-maximizing quantity is always q∗ where MR(q) = MC(q)

  • But monopolist faces entire market demand

    • Can charge as high as consumers are WTP Market Demand

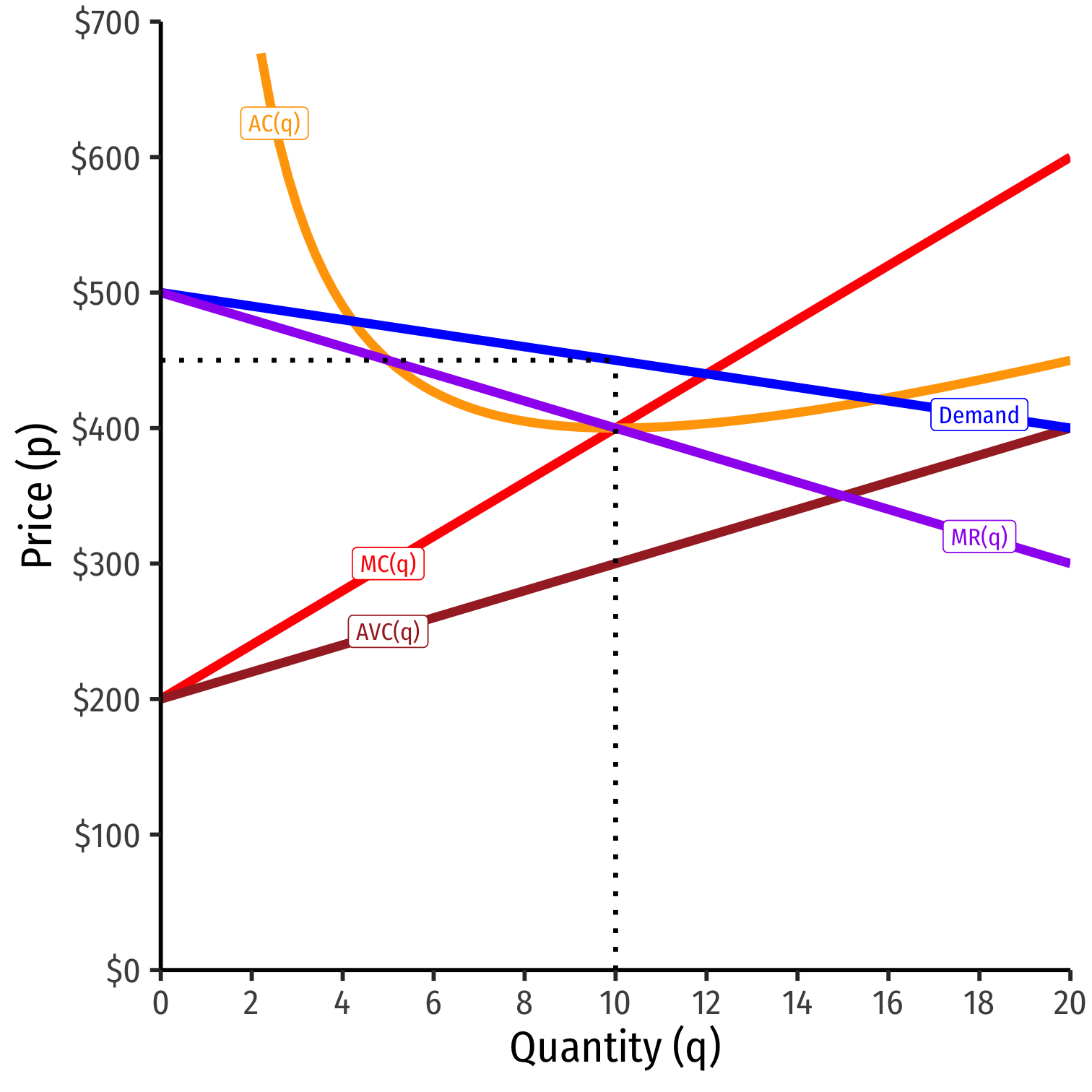
Profit-Maximizing Price and Quantity (Graph)

  • Profit-maximizing quantity is always q∗ where MR(q) = MC(q)

  • But monopolist faces entire market demand

    • Can charge as high as consumers are WTP Market Demand

  • Break even price p=AC(q)min

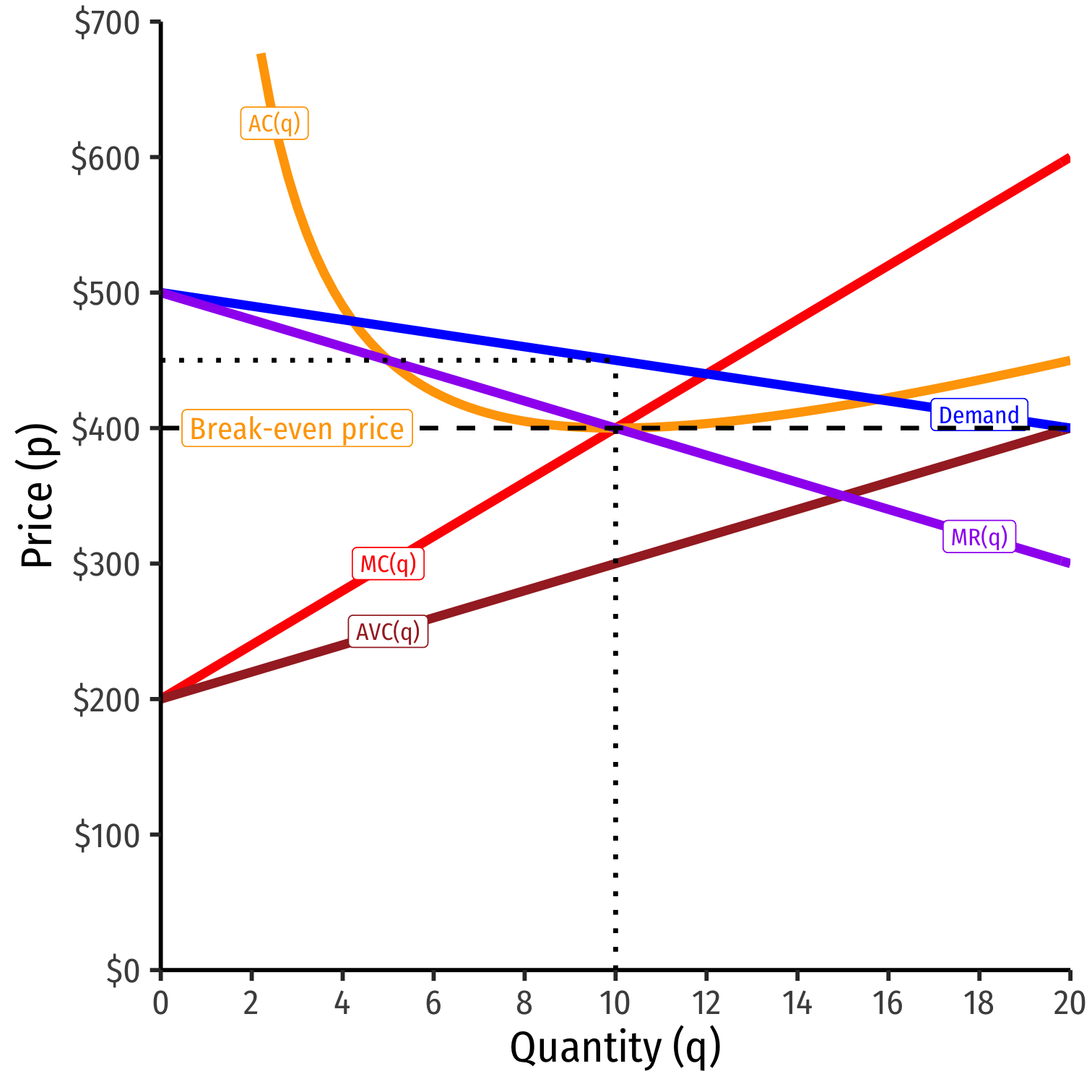
Profit-Maximizing Price and Quantity (Graph)

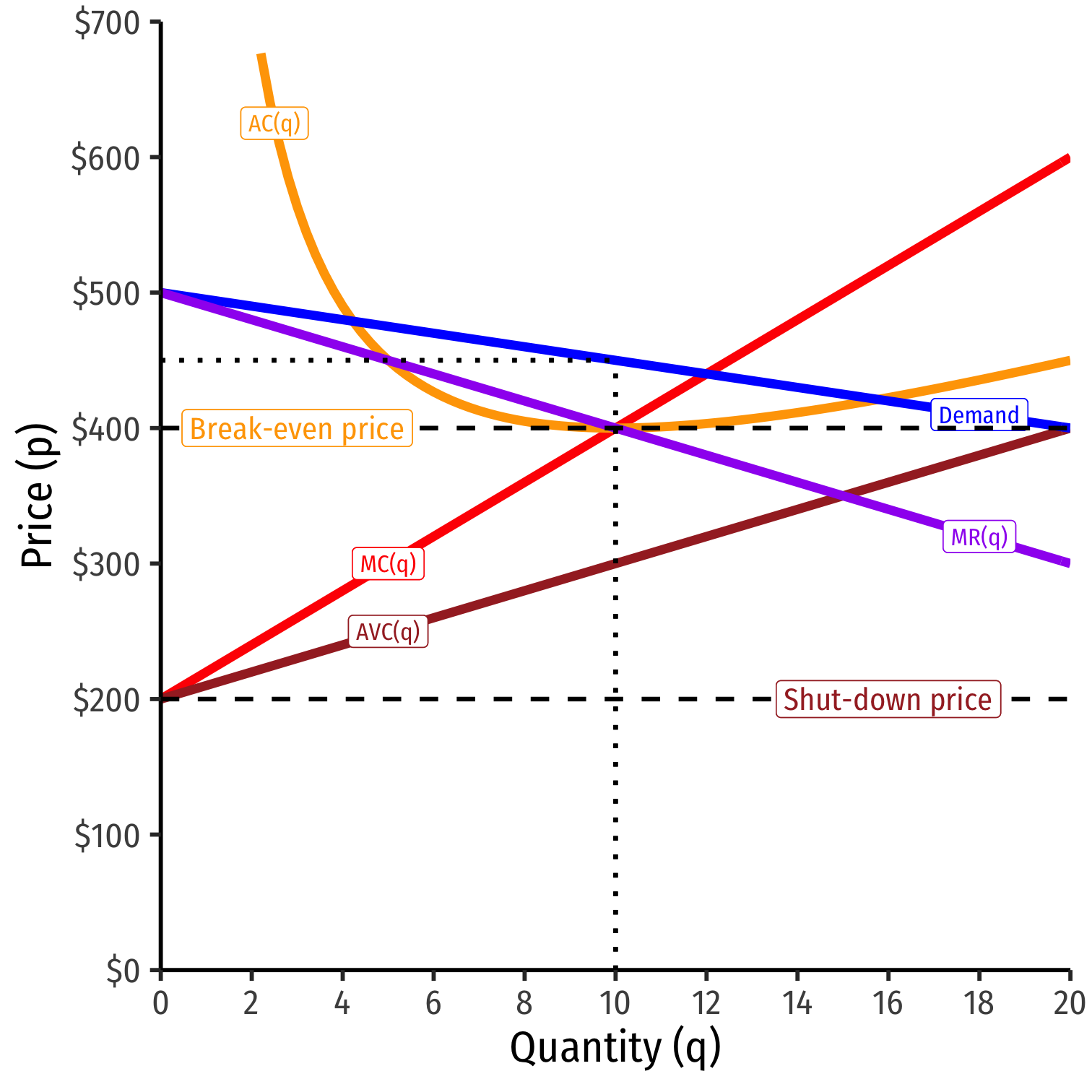
  • Profit-maximizing quantity is always q∗ where MR(q) = MC(q)

  • But monopolist faces entire market demand

    • Can charge as high as consumers are WTP Market Demand

  • Break even price p=AC(q)min

  • Shut-down price p=AVC(q)min

Monopolist's Supply Decisions

  1. Produce the optimal amount of output q∗ where MR(q)=MC(q)

Monopolist's Supply Decisions

  1. Produce the optimal amount of output q∗ where MR(q)=MC(q)

  2. Raise price to maximum consumers are WTP: p∗=Demand(q∗)

Monopolist's Supply Decisions

  1. Produce the optimal amount of output q∗ where MR(q)=MC(q)

  2. Raise price to maximum consumers are WTP: p∗=Demand(q∗)

  3. Calculate profit with average cost: π=[p−AC(q)]q

Monopolist's Supply Decisions

  1. Produce the optimal amount of output q∗ where MR(q)=MC(q)

  2. Raise price to maximum consumers are WTP: p∗=Demand(q∗)

  3. Calculate profit with average cost: π=[p−AC(q)]q

  4. Shut down in the short run if p<AVC(q)

    • Minimum of AVC curve where MC(q)=AVC(q)

Monopolist's Supply Decisions

  1. Produce the optimal amount of output q∗ where MR(q)=MC(q)

  2. Raise price to maximum consumers are WTP: p∗=Demand(q∗)

  3. Calculate profit with average cost: π=[p−AC(q)]q

  4. Shut down in the short run if p<AVC(q)

    • Minimum of AVC curve where MC(q)=AVC(q)

  5. Exit in the long run if p<AC(q)

    • Minimum of AC curve where MC(q)=AC(q)

The Profit Maximizing Quantity & Price: Example

Example: Consider the market for iPhones. Suppose Apple's costs are:

C(q)=2.5q2+25,000MC(q)=5q

The demand for iPhones is given by (quantity is in millions of iPhones):

q=300−0.2p

  1. Find Apple's profit-maximizing quantity and price.
  2. How much total profit does Apple earn?
  3. How much of Apple's price is markup over (marginal) cost?
  4. What is the price elasticity of demand at Apple's profit-maximizing output?

Outline

Market Power

Marginal Revenue

Price Elasticity & Price Mark Up

Profit Maximization Rules, Redux

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow